
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над векторамиСодержание книги
Поиск на нашем сайте
1) Сложение вектора производится по правилу параллелограмма: векторы 2)Разностью двух векторов Векторы можно не только складывать и вычитать, но и умножать на числа (скаляры). Вектор 1. 2.длина вектора при Произведение вектора на скаляр обладает следующими свойствами: 1. 4. Линейная зависимость векторов Говорят, что векторы линейно независимы, если из равенства:
следует, что В противном случае векторы Колинеальные векторы всегда линейно зависимы Если среди векторов есть хоть один нулевой вектор, но они линейно зависимы Если среди векторов есть несколько линейно зависимых, то векторы будут линейно зависимы Векторы параллельные одной плоскости -компланарные Если 3 вектора не нулевые и не компланарны, то они линейно не зависимы Любые 4 вектора линейно зависимы, если есть среди них 3 компланарых Базис — множество векторов в линейном пространстве, таких, что любой вектор пространства может быть единственным образом представлен в виде их линейной комбинации. Декартовы прямоугольные координаты в пространстве. Координаты точек. Координаты векторов. Деление отрезка в данном отношении Декартова прямоугольная система координат в пространстве определяется заданием единицы масштаба для измерения длин и трех пересекающихся в точке взаимно перпендикулярных осей, первая из которых называется осью абсцисс 2.Различные формы произведения векторов. Условие ортогональности, коллинеарности и компланарности векторов.
Скалярное произведение Скалярными произведением (a,b) двух векторов Скалярное произведение обладает следующими свойствами: 1. 3. Если Скалярный квадрат вектора Векторное произведение Векторным произведением вектора 1. 2. 3. Векторное произведение обладает следующими свойствами: 1. 2. Векторное произведение равно нулю (нуль вектору) тогда и только тогда, когда Если Смешанное произведение Смешанным произведением тройки векторов Таким образом, смешанное произведение векторов Знак произведение положителен, если векторы Из геометрического смысла смешанного произведения непосредственно следует необходимое и достаточное условие некомпланарности векторов
Определение. Вектора a и b называются ортогональными, если угол между ними равен 90°.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.80.161 (0.007 с.) |

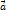 и
и 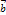 сносятся в общую точку
сносятся в общую точку 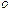 на них строят параллелограмм
на них строят параллелограмм 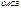 и его диагональ
и его диагональ 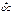 называют суммой векторов
называют суммой векторов  является вектор, направленный из конца вычитаемого вектора
является вектор, направленный из конца вычитаемого вектора 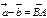
 равен
равен 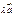 , где
, где  ‑ некоторое число, если:
‑ некоторое число, если: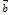 коллинеарен
коллинеарен  ;
;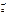 в
в 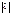 раз,
раз, ,
,  направлены в одну сторону, при
направлены в одну сторону, при 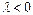 ‑ в разные.
‑ в разные.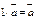 ; 2.
; 2. 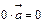 ; 3.
; 3. 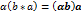
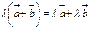 .
.
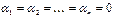 .
.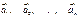 называются линейно зависимыми. Если какой-нибудь вектор можно представить в виде
называются линейно зависимыми. Если какой-нибудь вектор можно представить в виде  , то говорят, что вектор
, то говорят, что вектор 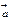 линейно выражается через векторы
линейно выражается через векторы  .
.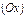 , вторая – осью ординат
, вторая – осью ординат 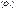 , третья – осью аппликат
, третья – осью аппликат 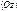 ; точка
; точка  ‑ начало координат. Положение координатных осей можно задать с помощью единичных векторов
‑ начало координат. Положение координатных осей можно задать с помощью единичных векторов 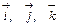 , направленных соответственно по осям
, направленных соответственно по осям 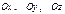 . Векторы
. Векторы 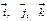 называются основными или базисными ортами и определяют базис
называются основными или базисными ортами и определяют базис 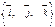 в трехмерном пространстве.
в трехмерном пространстве.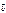 называется число, равное произведению их длин на косинус угла между ними:
называется число, равное произведению их длин на косинус угла между ними: 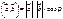 .
.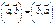 ; 2.
; 2. 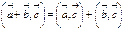 ;
; ;
;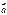 и
и  - острый, если (a,b)<0, то угол - тупой;
- острый, если (a,b)<0, то угол - тупой; . Следовательно,
. Следовательно, 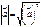 .
.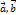 ], длина и направление которого определяется условиями:
], длина и направление которого определяется условиями: , где
, где 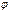 ‑ угол между
‑ угол между 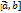 перпендикулярен каждому из векторов
перпендикулярен каждому из векторов 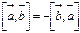 3.
3. 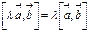
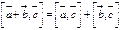
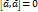 для любого вектора
для любого вектора 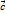 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 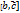 . Если рассматриваемые векторы
. Если рассматриваемые векторы  (которое обозначается
(которое обозначается 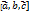 ) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах
) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах 


