
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В функциональном анализе существует обобщение понятия дифференцирования на случай отображений бесконечномерных пространств — производные гато и фреше.Содержание книги
Поиск на нашем сайте
Правило Лопиталя и формула Тейлора. Правила Лопиталя Пусть I правило. Если: 1. 2.Существует конечный или бесконечный предел II правило. Если: 1. 2.Существует конечный или бесконечный предел Правила Лопиталя позволяют раскрывать неопределенности вида Формула Тейлора Теорема. Пусть функция
Полученный многочлен называется формулой Тейлора Если
Для остаточного члена формулы Тейлора существуют и другие представления. Так, если функция
Исследование функции на экстремум, монотонность и точки перегиба функции. Монотонность функции Функция Теорема. Если функция Дифференцируемая функция является возрастающей на промежутке Выпуклость и перегибы графика функции Графиком функции Если на промежутке Точка I правило. Если II правило. Если Локальный экстремум Точка Точка Точки локального минимума и локального максимума называются точками локального экстремума. Необходимым условием локального экстремума дифференцируемой функции является выполнение равенства Решения этого уравнения называют стационарными точками.
Глобальный экстремум Непрерывная на отрезке - Находят стационарные точки - Находят точки - Вычисляют значения:
Это и будут
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.140 (0.005 с.) |

 и
и  - функции, определенные и дифференцируемые в окрестности точки a, где a - конечное число или
- функции, определенные и дифференцируемые в окрестности точки a, где a - конечное число или 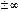 (если
(если  , то под окрестностью точки a понимаем какой-нибудь л
, то под окрестностью точки a понимаем какой-нибудь л  ; если
; если  , то окрестность – луч
, то окрестность – луч  ). В самой точке a функции могут быть не определены. Пусть
). В самой точке a функции могут быть не определены. Пусть  при
при  .
.
 . Тогда:
. Тогда:  .
. ;
; Тогда:
Тогда:  .
. или
или 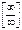 . Однако, они могут быть использованы и при раскрытии неопределенностей других видов:
. Однако, они могут быть использованы и при раскрытии неопределенностей других видов:  . Для этого исследуемое выражение преобразуют так, чтобы получилась неопределенность вида
. Для этого исследуемое выражение преобразуют так, чтобы получилась неопределенность вида  или
или  .
. определена в некоторой окрестности точки
определена в некоторой окрестности точки 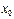 и
и  раз дифференцируема в ней. Тогда, при
раз дифференцируема в ней. Тогда, при  имеет место формула:
имеет место формула: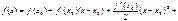

 -го порядка с остаточным членом в форме Пеано.
-го порядка с остаточным членом в форме Пеано. , то формула Тейлора называется формулой Маклорена и имеет вид:
, то формула Тейлора называется формулой Маклорена и имеет вид:
 имеет производную
имеет производную  –го порядка в окрестности точки
–го порядка в окрестности точки  , то остаточный член может быть представлен в форме Лагранжа:
, то остаточный член может быть представлен в форме Лагранжа: ,
,  .
. называется возрастающей на промежутке
называется возрастающей на промежутке  , если
, если  для любых точек
для любых точек  и
и  из промежутка
из промежутка  , удовлетворяющих неравенству
, удовлетворяющих неравенству  . Функция называется убывающей на
. Функция называется убывающей на  , если из условия
, если из условия 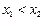 следует
следует 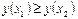 .
. непрерывна на отрезке
непрерывна на отрезке  , дифференцируема на интервале
, дифференцируема на интервале  , то для того, чтобы
, то для того, чтобы 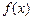 была возрастающей (убывающей) необходимо и достаточно, чтобы
была возрастающей (убывающей) необходимо и достаточно, чтобы 
 в каждой внутренней точке интервала
в каждой внутренней точке интервала  .
. тогда и только тогда, когда
тогда и только тогда, когда  .
. , заданной на множестве
, заданной на множестве 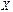 , называют множество точек плоскости с координатами
, называют множество точек плоскости с координатами  . График называют выпуклым вниз на промежутке
. График называют выпуклым вниз на промежутке  , если касательная к графику в любой точке этого промежутка расположена ниже графика. Если касательная расположена выше графика, то график называют выпуклым вверх. Точка, в которой график меняет направление выпуклости, называется точкой перегиба.
, если касательная к графику в любой точке этого промежутка расположена ниже графика. Если касательная расположена выше графика, то график называют выпуклым вверх. Точка, в которой график меняет направление выпуклости, называется точкой перегиба. вторая производная
вторая производная  положительна, то график является выпуклым вниз на этом промежутке. Если
положительна, то график является выпуклым вниз на этом промежутке. Если  на промежутке
на промежутке  может быть точкой перегиба только в том случае, когда
может быть точкой перегиба только в том случае, когда 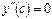 , либо
, либо  не существует – необходимое условие перегиба. Однако равенство нулю или не существование второй производной в точке
не существует – необходимое условие перегиба. Однако равенство нулю или не существование второй производной в точке  не означает еще, что в точке
не означает еще, что в точке  будет перегиб графика. Поэтому нужно дополнительно исследовать такие точки.
будет перегиб графика. Поэтому нужно дополнительно исследовать такие точки. равна нулю или не существует и
равна нулю или не существует и 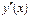 при переводе через точку
при переводе через точку 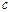 меняет знак, то
меняет знак, то  ‑ точка перегиба графика функции
‑ точка перегиба графика функции  .
. и
и  , то
, то 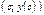 является точкой перегиба графика функции
является точкой перегиба графика функции  .
. называется точкой локального максимума функции
называется точкой локального максимума функции 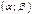 , содержащий точку
, содержащий точку  .
. называется точкой локального минимума функции
называется точкой локального минимума функции  , если существует интервал
, если существует интервал  , содержащий точку
, содержащий точку 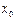 такой что
такой что  .
. . Поэтому точки, в которых дифференцируемая функция может иметь локальный экстремум, находят, решая уравнение:
. Поэтому точки, в которых дифференцируемая функция может иметь локальный экстремум, находят, решая уравнение:  .
. функция
функция  принимает свое наибольшее значение
принимает свое наибольшее значение  и свое наименьшее значение
и свое наименьшее значение  в точках этого отрезка. Эти значения могут достигаться либо в стационарных точках отрезка, либо в точках недифференцируемости функции, либо в граничных точках отрезка. Поэтому для нахождения значений
в точках этого отрезка. Эти значения могут достигаться либо в стационарных точках отрезка, либо в точках недифференцируемости функции, либо в граничных точках отрезка. Поэтому для нахождения значений  и
и  поступают следующим образом.
поступают следующим образом. функции;
функции; , в которых производная
, в которых производная 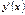 не существует или обращается в бесконечность;
не существует или обращается в бесконечность; ‑ и выбирают среди этих чисел наибольшее и наименьшее.
‑ и выбирают среди этих чисел наибольшее и наименьшее. и
и  ‑ глобальные экстремальные значения.
‑ глобальные экстремальные значения.


