
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел функции. Понятие непрерывности и свойства функций, непрерывных в точке. Точки разрыва. Замечательные пределы. Сравнение бесконечно малых.Содержание книги
Поиск на нашем сайте
Непрерывность функции Рассмотрим функцию
Функция Функция Функция Общие свойства непрерывных функций, заданных на отрезке Теорема (первая теорема Больцано–Коши). Пусть функция Теорема (вторая теорема Больцано–Коши). Пусть функция т.е. Теорема (первая теорема Вейерштрасса). Пусть функция Теорема (вторая теорема Вейерштрасса). Пусть функция Точки разрыва Непрерывность функции Если условие (4) не выполнено, то точку 1. 2. 3. 4. Если 1. не выполнено, то Если 1. выполнено, а 2. не выполнено, то Если выполнены 1. и 2., а 3. не выполнено, то
Если 1., 2., 3. выполнены, а 4. не выполнено, то Если функция Сравнение бесконечно малых величин: - Две бесконечно малые величины
- Величина - Величина - Две бесконечно малые величины Функции, непрерывные на отрезке, и их свойства. Равномерная непрерывность. Равномерная непрерывность важное понятие математического анализа. Функция f (x) называется равномерно-непрерывной на данном множестве, если для всякого ε > 0 можно найти такое δ = δ(ε) > 0, что | f (x 1) — f (x 2)|<ε для любой пары чисел x 1 и x 2 из данного множества, удовлетворяющей условию | x 1 —x 2|< δ (ср. Непрерывная функция).Например, функция f (x) = x 2 равномерно непрерывна на отрезке [0, 1]: если
Так, например, функция непрерывна в каждой точке интервала 0 < x < 1, но не является равномерно непрерывной в этом интервале, потому что, например, при ε = 1 для любого δ > 0 (δ < 1) мы имеем удовлетворяющие неравенству |x1 — x2| < δ числа x1 = Понятие производной, ее геометрический и физический смысл. Основные правила дифференцирования. Таблица производных.
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.176.136 (0.009 с.) |

 , определенную на промежутке
, определенную на промежутке  Пусть
Пусть  . Функция
. Функция  называется непрерывной в точке
называется непрерывной в точке 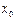 , если
, если 
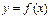 называется непрерывной слева (справа) в точке
называется непрерывной слева (справа) в точке 
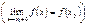 . Естественно, при этом функция
. Естественно, при этом функция 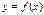 должна быть определена в некоторой окрестности слева (справа) то точки
должна быть определена в некоторой окрестности слева (справа) то точки 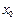 означает непрерывность этой функции в указанной точке как слева, так и справа.
означает непрерывность этой функции в указанной точке как слева, так и справа.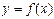 , определенная на интервале
, определенная на интервале  называется непрерывной на интервале
называется непрерывной на интервале 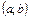 , если она непрерывна в каждой точке
, если она непрерывна в каждой точке 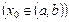 .
. , определенная на отрезке
, определенная на отрезке 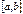 (
(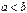 ) называется непрерывной на отрезке
) называется непрерывной на отрезке 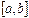 , если она непрерывна в каждой точке
, если она непрерывна в каждой точке  интервала
интервала 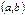 , непрерывна справа в точке b и непрерывна слева в точке a.
, непрерывна справа в точке b и непрерывна слева в точке a.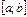 , определяются четырьмя теоремами: двумя теоремами Больцано–Коши и двумя теоремами Вейерштрасса.
, определяются четырьмя теоремами: двумя теоремами Больцано–Коши и двумя теоремами Вейерштрасса.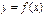 определена и непрерывна на отрезке
определена и непрерывна на отрезке 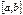 , и на концах этого промежутка принимает значения разных знаков; тогда найдется точка
, и на концах этого промежутка принимает значения разных знаков; тогда найдется точка 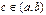 , в которой функция равна нулю.
, в которой функция равна нулю. определена и непрерывна на отрезке
определена и непрерывна на отрезке 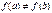 то функция принимает все свои промежуточные значения, принадлежащие промежутку
то функция принимает все свои промежуточные значения, принадлежащие промежутку  , где
, где 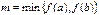 ,
, 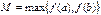 ,
,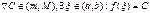 .
. определена и непрерывна на отрезке
определена и непрерывна на отрезке 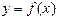 является ограниченной на этом отрезке.
является ограниченной на этом отрезке.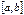 , тогда функция
, тогда функция 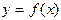 имеет минимум и максимум на этом отрезке (множество значений функции включает в себя точные верхнюю и нижнюю границы).
имеет минимум и максимум на этом отрезке (множество значений функции включает в себя точные верхнюю и нижнюю границы).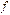 в точке
в точке 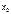 , т.е. выполнение условия (3), означает, что оба односторонних предела
, т.е. выполнение условия (3), означает, что оба односторонних предела 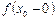 и
и 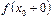 существуют и равны
существуют и равны 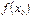 , т.е.
, т.е. 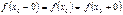
 называют точкой разрыва функции
называют точкой разрыва функции 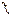 . Условие (4) означает выполнение следующих четырех условий, каждое из которых предполагает выполнение всех предыдущих:
. Условие (4) означает выполнение следующих четырех условий, каждое из которых предполагает выполнение всех предыдущих: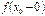 и
и 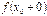 существуют;
существуют; и
и 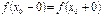 ;
; .
. называют точкой конечного скачка. Величина
называют точкой конечного скачка. Величина  называется скачком функции
называется скачком функции 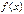 в точке
в точке 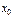 .
.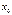 называют точкой устранимого разрыва.
называют точкой устранимого разрыва.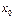 и не определена в самой точке
и не определена в самой точке 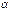 и
и 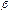 называются бесконечно малыми одного порядка, если предел их отношения есть конечное число, отличное от нуля, т.е.
называются бесконечно малыми одного порядка, если предел их отношения есть конечное число, отличное от нуля, т.е.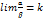 ;
; 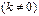
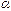 называется бесконечно малой величиной высшего порядка по сравнению с
называется бесконечно малой величиной высшего порядка по сравнению с  , если предел отношения
, если предел отношения  к
к 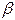 равен нулю, т.е.
равен нулю, т.е. 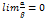 ;
;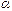 называется бесконечно малой величиной низшего порядка по сравнению с
называется бесконечно малой величиной низшего порядка по сравнению с 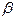 , если предел отношения
, если предел отношения 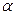 к
к 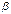 является бесконечно большой величиной, т.е.
является бесконечно большой величиной, т.е. 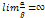 ;
;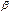 называются эквивалентными бесконечно малыми, если предел их отношения равен единице, т.е.
называются эквивалентными бесконечно малыми, если предел их отношения равен единице, т.е. 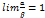 .
. x1 ≤ 1, 0 ≤ x2 ≤ 1 обязательно |x1 + x2|≤ 2). Вообще функция, непрерывная в каждой точке отрезка [а, b], равномерно непрерывна на этом отрезке (теорема Кантора). Для интервала эта теорема может не иметь места.
x1 ≤ 1, 0 ≤ x2 ≤ 1 обязательно |x1 + x2|≤ 2). Вообще функция, непрерывная в каждой точке отрезка [а, b], равномерно непрерывна на этом отрезке (теорема Кантора). Для интервала эта теорема может не иметь места. 
 и x2= δ, для которых
и x2= δ, для которых 



