
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение и смысл производнойСодержание книги
Поиск на нашем сайте
Понятие производной является одним из основных понятий дифференциального исчисления, производная используется при исследовании процессов, в том числе и экономических, описываемых функциями. При исследовании приращения зависимой величины Физический смысл производной. Если функция y = f(x) и ее аргумент x являются физическими величинами, то производная – скорость изменения переменной y относительно переменной x в точке. Например, если S = S(t) – расстояние, проходимое точкой за время t, то ее производная – скорость в момент времени. Если q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t, то – скорость изменения количества электричества в момент времени, т.е. сила тока в момент времени. Геометрический смысл производной. Пусть L – некоторая кривая,M0 – точка на кривой L. Любая прямая, пересекающая L не менее чем в двух точках называется секущей. Касательной к кривой Lв точке M0 называется предельное положение секущей M0M1, если точка M1 стремится к M0, двигаясь по кривой. Из определения очевидно, что если касательная к кривой в точке M0существует, то она единственная Правила дифференцирования Будем считать, что функции 1.Функция 2.Если 3.Из 1 и 2 следует, что 4.Функция 5.Из 4 следует, что 6.Если Таблица производных Основные элементарные функции дифференцируемы всюду, где они определены. Производные этих функций могут быть вычислены по определению, т.е. по формуле:
и с помощью правил дифференцирования. Полученные значения производных основных элементарных функций приведем в таблице.
Дифференциал и его применения. Производные и дифференциалы высших порядков. Производные высших порядков Если функция К этой функции применимы все предельные законы, в том числе и дифференцирование. Если Аналогично вычисляются производные более высоких порядков. 21.Свойства функций, дифференцируемых на отрезке. Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является одним из фундаментальных понятий в математике и имеет значительное число приложений как в самой математике, так и в других естественных науках. Приращение дифференцируемой в данной точке функции можно представить как линейную функцию приращения аргумента с точностью до величин более высокого порядка малости. Это означает, что для достаточно малых окрестностей данной точки функцию можно заменить линейной (скорость изменения функции можно считать неизменной). Линейная часть приращения функции называется ее дифференциалом (в данной точке). Необходимым, но не достаточным условием дифференцируемости является непрерывность функции. В случае функции от одной вещественной переменной дифференцируемость равносильна существованию производной. В случае функции нескольких вещественных переменных необходимым (но не достаточным) условием дифференцируемости является существование частных производных по всем переменным. Для дифференцируемости функции нескольких переменных в точке достаточно, чтобы частные производные существовали в некоторой окрестности рассматриваемой точки и были непрерывны в данной точке.[1] В случае функции комплексной переменной дифференцируемость в точке часто называется моногенностью и существенно отличается от понятия дифференцируемости в вещественном случае. Ключевую роль в этом играет так называемое условие Коши — Римана. Функция, моногенная в окрестности точки, называется голоморфной в этой точке.[2][3]
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.178.16 (0.009 с.) |

 , обусловленного приращением независимой переменной
, обусловленного приращением независимой переменной 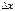 , часто возникает необходимость определения предела отношения этих величин
, часто возникает необходимость определения предела отношения этих величин  . Этот предел называется производной, а операция его вычисления – дифференцированием функции.
. Этот предел называется производной, а операция его вычисления – дифференцированием функции. дифференцируемы, т.е. имеют производные
дифференцируемы, т.е. имеют производные  . Тогда:
. Тогда: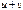 дифференцируема и
дифференцируема и  ;
; ‑ постоянная, то функция
‑ постоянная, то функция  дифференцируема и
дифференцируема и 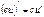 ;
; ;
; дифференцируема и
дифференцируема и  ;
; ;
; определена и диф-ма, то
определена и диф-ма, то 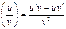 .
.
 ;
;  ;
; 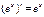 ;
; 
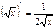 ;
;  ;
; 
 ;
;  ;
; 
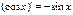 ;
;  ;
; 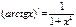
 ;
; 
 .
.
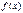 , определенная в
, определенная в  , имеет производную во всех точках
, имеет производную во всех точках  , то эту производную можно рассматривать как новую функцию
, то эту производную можно рассматривать как новую функцию  ,
, 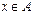 .
.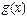 , определенная в
, определенная в  , имеет конечную производную
, имеет конечную производную  в точке
в точке  , то значение этой производной является второй производной функции
, то значение этой производной является второй производной функции  .
.


