
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторы. Линейные операции над ними. Зависимость векторов. Базис. Декартова система координат. Деление отрезка в данном отношении.Содержание книги
Поиск на нашем сайте
Векторы. Линейные операции над ними. Зависимость векторов. Базис. Декартова система координат. Деление отрезка в данном отношении. Вектором наз. направленный отрезок опред-ся длиной и направлением в пространстве, Линейные операции над векторами 1) Сложение вектора производится по правилу параллелограмма: векторы 2)Разностью двух векторов Векторы можно не только складывать и вычитать, но и умножать на числа (скаляры). Вектор 1. 2.длина вектора при Произведение вектора на скаляр обладает следующими свойствами: 1. 4. Линейная зависимость векторов Говорят, что векторы линейно независимы, если из равенства:
следует, что В противном случае векторы Колинеальные векторы всегда линейно зависимы Если среди векторов есть хоть один нулевой вектор, но они линейно зависимы Если среди векторов есть несколько линейно зависимых, то векторы будут линейно зависимы Векторы параллельные одной плоскости -компланарные Если 3 вектора не нулевые и не компланарны, то они линейно не зависимы Любые 4 вектора линейно зависимы, если есть среди них 3 компланарых Базис — множество векторов в линейном пространстве, таких, что любой вектор пространства может быть единственным образом представлен в виде их линейной комбинации. Декартовы прямоугольные координаты в пространстве. Координаты точек. Координаты векторов. Деление отрезка в данном отношении Декартова прямоугольная система координат в пространстве определяется заданием единицы масштаба для измерения длин и трех пересекающихся в точке взаимно перпендикулярных осей, первая из которых называется осью абсцисс
2.Различные формы произведения векторов. Условие ортогональности, коллинеарности и компланарности векторов. Скалярное произведение Скалярными произведением (a,b) двух векторов Скалярное произведение обладает следующими свойствами: 1. 3. Если Скалярный квадрат вектора Векторное произведение Векторным произведением вектора 1. 2. 3. Векторное произведение обладает следующими свойствами: 1. 2. Векторное произведение равно нулю (нуль вектору) тогда и только тогда, когда Если Смешанное произведение Смешанным произведением тройки векторов Таким образом, смешанное произведение векторов
Знак произведение положителен, если векторы Из геометрического смысла смешанного произведения непосредственно следует необходимое и достаточное условие некомпланарности векторов Определение. Вектора a и b называются ортогональными, если угол между ними равен 90°. Определение. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами Два вектора будут коллинеарны при выполнении любого из этих условий: Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. Всегда возможно найти плоскости параллельную двум произвольным векторам, по-этому любые два вектора всегда компланарные. Условия компланарности векторов Для 3-х векторов. Три вектора компланарны если их смешанное произведение равно нулю. Для 3-х векторов. Три вектора компланарны если они линейно зависимы. Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.
3.Определители второго и третьего порядка и их свойства. Определители n- го порядка и их свойства. Определители 2-ого и 3-его порядка это число. Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом
Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом
Операции над матрицами Суммой двух матриц Сложение матриц обладает следующими свойствами: 1.Коммутативность, т.е. 2.Ассоциативность, т.е. 3.Для любых двух матриц Произведением матрицы Умножение матрицы на действительное число обладает следующими свойствами: 1. 4. 5. 6. Матрица Свойства умножения: 1.Если матрица 2. 3.Умножение матриц не коммутативно, т.е., как правило, Обратная матрица Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Матрица, обратная матрице А, обозначается через А 1 , так что В = А 1 . Обратная матрица вычисляется по формуле
Вычисление обратной матрицы по формуле для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы. Ранг матрицы Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы A обозначают Если все миноры порядка Если все миноры первого порядка (элементы матрицы Метод Гаусса Метод Гаусса основан на теореме: если к некоторому уравнению системы прибавить другое уравнение этой системы, умноженное на любое действительное число, или умножить любое уравнение системы на отличное от нуля действительное число, то полученная система будет эквивалентна исходной. Метод Гаусса называют также методом последовательного исключения неизвестных, осуществляя его за несколько итераций. На каждой итерации выбирается разрешающее уравнение и базисное неизвестное. В качестве разрешающего уравнения можно взять любое уравнение системы, которое ранее не было выбрано разрешающим и не все коэффициенты которого равны нулю. За базисное неизвестное выбирают неизвестное, коэффициент при котором в разрешающем уравнении, называемый разрешающим коэффициентом, не равен нулю.
Алгоритм метода следующий: 1.Выбирают разрешающее уравнение и базисное неизвестное. 2.Делят обе части разрешающего уравнения на разрешающий коэффициент и исключают базисное неизвестное из всех уравнений системы, кроме разрешающего. Отбрасывают, если они появились, уравнения, все коэффициенты и свободный член в котором равны нулю. Если получилось уравнение, в котором коэффициенты нулевые, а свободный член не нуль, то система несовместна, конец. Если таких уравнений нет, то шаг 1. Если все уравнения были использованы в качестве разрешающих, то шаг 3.Если нет, то шаг 1. 4.Базисные неизвестные оставляют слева, а небазисные (назовем их свободными, так как они могут принимать любые значения) переносят вправо. Норма вектора Норма в векторном пространстве 1. 2. 3. Эти условия являются аксиомами нормы. Из 3 получаем, что
Любой ненулевой вектор Линейные операторы в евклидовом пространстве. Сопряженные и самосопряженные операторы. Собственные векторы и собственные значения. Канонический вид матрицы. Операторы в евклидовом пространстве и их продолжение на комплексификацию. В евклидовом пространстве для оператора 9 определяется сопряженный оператора 10 той же формулой 11 при любых х и у, что и в унитарном пространстве. Доказательство существования и единственности сопряженного оператора ничем не отличается от аналогичных доказательств для унитарного пространства. Матрица оператора 12 в ортонормальном базисе просто транспонирована с матрицей оператора 13 При продолжении взаимно сопряженных операторов 14 с S на 15 они останутся сопряженными. Действительно,
Нормальный оператор 16 в евклидовом пространстве S остается нормальным и при его продолжении на комплексификацию 17 пространства S. Поэтому в S существует ортонормальный базис из собственных векторов, диагонализующий матрицу оператора А. Для вещественных собственных значений можно взять вещественные собственные векторы, т. е. лежащие в S. Действительно, координаты собственных векторов относительно базиса 18 определяются из линейных однородных уравнений с вещественными коэффициентами в случае вещественности собственного значения. Комплексные собственные значения появляются парами сопряженных с одинаковой кратностью. Выбрав ортонормальный базис из собственных векторов, принадлежащих некоторому собственному значению 19 при 20 базис из собственных векторов для собственного значения 21 можно взять из векторов, сопряженных с векторами базиса собственных значений для X. Такой базис будет ортонормальный. Теперь натянем на каждую пару и 22 сопряженных векторов двумерное комплексное подпространство.
Для самосопряженных операторов в евклидовом пространстве имеют место те же свойства, которые отмечались для самосопряженных операторов в унитарном пространстве, и их доказательства ничем не отличаются от доказательств в случае унитарного пространства. Понятие квадратичной формы Первоначально теория квадратичных форм использовалась для исследования кривых и поверхностей, задаваемых уравнением второго порядка, содержащими две или три переменные, Позднее эта теория нашла и другие приложения. В частности, при математическом моделировании экономических процессов целевые функции могут содержать квадратичные слагаемые. Многочисленные приложения квадратичных форм потребовали построения общей теории, когда число переменных равно любому Квадратичной формой Бесконечный предел Наряду с бесконечно малыми существуют и бесконечно большие величины, являющиеся обратными по отношению к бесконечно малым. Поэтому Говорят, что предел последовательности В отличие от бесконечно малых последовательностей, бесконечно большие могут не иметь предела. Например, Свойства пределов: Пределы обладают следующими свойствами: - Если - Если существуют - Если существуют - Если существуют - Если существуют - Если Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей. Число «e» — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики. Непрерывность функции Рассмотрим функцию
Функция Функция Функция Общие свойства непрерывных функций, заданных на отрезке Теорема (первая теорема Больцано–Коши). Пусть функция Теорема (вторая теорема Больцано–Коши). Пусть функция т.е. Теорема (первая теорема Вейерштрасса). Пусть функция Теорема (вторая теорема Вейерштрасса). Пусть функция Точки разрыва Непрерывность функции Если условие (4) не выполнено, то точку 1. 2. 3. 4. Если 1. не выполнено, то Если 1. выполнено, а 2. не выполнено, то Если выполнены 1. и 2., а 3. не выполнено, то Если 1., 2., 3. выполнены, а 4. не выполнено, то Если функция Сравнение бесконечно малых величин: - Две бесконечно малые величины
- Величина - Величина - Две бесконечно малые величины Понятие производной, ее геометрический и физический смысл. Основные правила дифференцирования. Таблица произво |
|||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.163.78 (0.01 с.) |

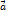 и
и 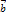 сносятся в общую точку
сносятся в общую точку 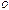 на них строят параллелограмм
на них строят параллелограмм 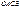 и его диагональ
и его диагональ 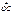 называют суммой векторов
называют суммой векторов  является вектор, направленный из конца вычитаемого вектора
является вектор, направленный из конца вычитаемого вектора 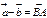
 равен
равен 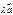 , где
, где  ‑ некоторое число, если:
‑ некоторое число, если: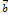 коллинеарен
коллинеарен  ;
;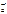 в
в 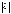 раз,
раз, ,
,  направлены в одну сторону, при
направлены в одну сторону, при 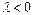 ‑ в разные.
‑ в разные.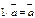 ; 2.
; 2. 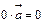 ; 3.
; 3. 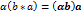
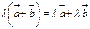 .
.
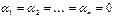 .
.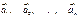 называются линейно зависимыми. Если какой-нибудь вектор можно представить в виде
называются линейно зависимыми. Если какой-нибудь вектор можно представить в виде  , то говорят, что вектор
, то говорят, что вектор 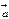 линейно выражается через векторы
линейно выражается через векторы  .
.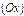 , вторая – осью ординат
, вторая – осью ординат 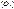 , третья – осью аппликат
, третья – осью аппликат 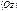 ; точка
; точка  ‑ начало координат. Положение координатных осей можно задать с помощью единичных векторов
‑ начало координат. Положение координатных осей можно задать с помощью единичных векторов 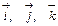 , направленных соответственно по осям
, направленных соответственно по осям 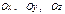 . Векторы
. Векторы 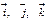 называются основными или базисными ортами и определяют базис
называются основными или базисными ортами и определяют базис 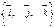 в трехмерном пространстве.
в трехмерном пространстве.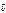 называется число, равное произведению их длин на косинус угла между ними:
называется число, равное произведению их длин на косинус угла между ними: 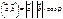 .
.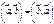 ; 2.
; 2. 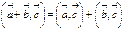 ;
; ;
;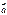 и
и  - острый, если (a,b)<0, то угол - тупой;
- острый, если (a,b)<0, то угол - тупой; . Следовательно,
. Следовательно, 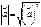 .
.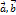 ], длина и направление которого определяется условиями:
], длина и направление которого определяется условиями: , где
, где 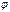 ‑ угол между
‑ угол между 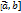 перпендикулярен каждому из векторов
перпендикулярен каждому из векторов 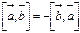 3.
3. 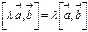
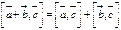
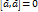 для любого вектора
для любого вектора 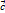 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 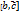 . Если рассматриваемые векторы
. Если рассматриваемые векторы  (которое обозначается
(которое обозначается 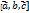 ) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах
) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах 
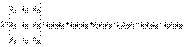
 и
и 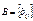 одинакового размера называется матрица
одинакового размера называется матрица 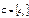 того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е.
того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е. 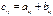 .
. .
.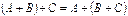 .
. и
и  одинакового размера существует единственная матрица
одинакового размера существует единственная матрица 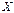 такая, что
такая, что  . Матрица
. Матрица 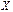 обозначается
обозначается 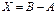 и называется разностью матриц
и называется разностью матриц 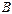 и
и 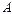 . Уравнение
. Уравнение 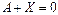 имеет решение
имеет решение  , получающаяся при этом матрица называется противоположной
, получающаяся при этом матрица называется противоположной 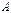 и обозначается
и обозначается 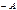 .
.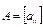 на число
на число  называется матрица, все элементы которой равны соответствующим элементам матрицы
называется матрица, все элементы которой равны соответствующим элементам матрицы 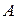 , умноженным на число
, умноженным на число  .
. ; 2.
; 2.  ; 3.
; 3. 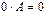 ;
; (ассоциативность);
(ассоциативность);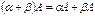 (дистрибутивность);
(дистрибутивность); (дистрибутивность).
(дистрибутивность).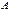 называется согласованной с матрицей
называется согласованной с матрицей  равно числу строк матрицы
равно числу строк матрицы 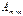 на матрицу
на матрицу 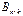 называется матрица
называется матрица  , где
, где 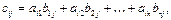
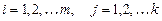 , т.е. элемент, стоящий в
, т.е. элемент, стоящий в  -той строке и
-той строке и  -том столбце матрицы произведения равен сумме произведений элементов
-том столбце матрицы произведения равен сумме произведений элементов 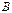 .
.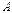 согласована с матрицей
согласована с матрицей 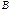 согласована с матрицей
согласована с матрицей 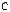 , то
, то 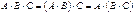 ‑ ассоциативность умножения;
‑ ассоциативность умножения;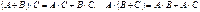 ‑ свойство дистрибутивности;
‑ свойство дистрибутивности; .
.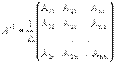 где А i j - алгебраические дополнения элементов a i j.
где А i j - алгебраические дополнения элементов a i j. .
. данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.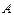 ) равны нулю, то
) равны нулю, то 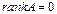 . Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то
. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то 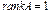 . Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка
. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка 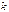 , окаймляющие ненулевой минор
, окаймляющие ненулевой минор 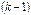 -го порядка равны нулю, либо таких миноров нет. Тогда
-го порядка равны нулю, либо таких миноров нет. Тогда 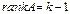 .
. над полем вещественных или комплексных чисел — это функционал
над полем вещественных или комплексных чисел — это функционал 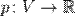 , обладающий следующими свойствами:
, обладающий следующими свойствами: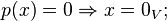
 (неравенство треугольника);
(неравенство треугольника);
 Теперь из 2 получаем
Теперь из 2 получаем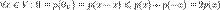 . Таким образом,
. Таким образом, 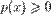 .
. . В частности,
. В частности, 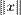 — это норма элемента
— это норма элемента  векторного пространства
векторного пространства 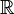 .
.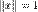 ) называется нормальным или нормированным.
) называется нормальным или нормированным.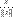 имеет единичную норму. С геометрической точки зрения это значит, что мы берем сонаправленный вектор единичной длины.
имеет единичную норму. С геометрической точки зрения это значит, что мы берем сонаправленный вектор единичной длины.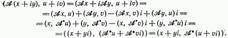
 , а коэффициенты квадратичной формы не всегда являются вещественными числами.
, а коэффициенты квадратичной формы не всегда являются вещественными числами.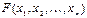 от
от  неизвестных
неизвестных 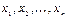 называется сумма, каждое слагаемое которой является либо квадратом одного из неизвестных, либо произведением двух разных неизвестных.
называется сумма, каждое слагаемое которой является либо квадратом одного из неизвестных, либо произведением двух разных неизвестных.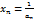 является бесконечно большой (
является бесконечно большой (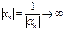 , при
, при  ), если
), если 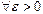
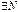 такое, что при
такое, что при 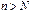
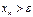 .
.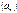 равен
равен 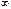 , если для
, если для 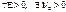 такое, что
такое, что 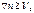 выполняется неравенство:
выполняется неравенство:  .
.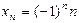 по модулю неограниченно растет, но сама величина
по модулю неограниченно растет, но сама величина 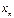 не имеет определенного стремления.
не имеет определенного стремления. – есть постоянная функция, то
– есть постоянная функция, то 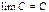 ;
; , и в некоторой окрестности точки
, и в некоторой окрестности точки 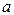 функция
функция 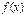 ограничена, т.е.
ограничена, т.е.  , тогда
, тогда  ;
;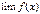 и
и  при каком-то условии, то
при каком-то условии, то 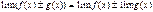 (при том же условии). Это свойство справедливо для любого конечного числа функций;
(при том же условии). Это свойство справедливо для любого конечного числа функций; и
и 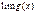 при каком-то условии, то
при каком-то условии, то 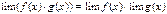 (при том же условии). Это свойство также справедливо для любого конечного числа функций, в частности, справедлива формула
(при том же условии). Это свойство также справедливо для любого конечного числа функций, в частности, справедлива формула 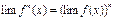 ;
;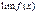 и
и 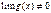 при каком-то условии, то
при каком-то условии, то 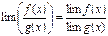 (при том же условии);
(при том же условии);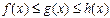 и существуют
и существуют 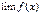 ,
, 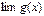 и
и  , то
, то 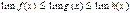 .
. , определенную на промежутке
, определенную на промежутке  Пусть
Пусть  . Функция
. Функция  называется непрерывной в точке
называется непрерывной в точке 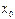 , если
, если 
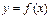 называется непрерывной слева (справа) в точке
называется непрерывной слева (справа) в точке 
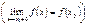 . Естественно, при этом функция
. Естественно, при этом функция 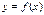 должна быть определена в некоторой окрестности слева (справа) то точки
должна быть определена в некоторой окрестности слева (справа) то точки 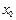 означает непрерывность этой функции в указанной точке как слева, так и справа.
означает непрерывность этой функции в указанной точке как слева, так и справа.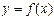 , определенная на интервале
, определенная на интервале  называется непрерывной на интервале
называется непрерывной на интервале 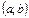 , если она непрерывна в каждой точке
, если она непрерывна в каждой точке 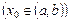 .
. , определенная на отрезке
, определенная на отрезке 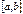 (
(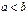 ) называется непрерывной на отрезке
) называется непрерывной на отрезке 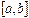 , если она непрерывна в каждой точке
, если она непрерывна в каждой точке  интервала
интервала 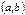 , непрерывна справа в точке b и непрерывна слева в точке a.
, непрерывна справа в точке b и непрерывна слева в точке a.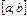 , определяются четырьмя теоремами: двумя теоремами Больцано–Коши и двумя теоремами Вейерштрасса.
, определяются четырьмя теоремами: двумя теоремами Больцано–Коши и двумя теоремами Вейерштрасса.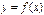 определена и непрерывна на отрезке
определена и непрерывна на отрезке 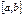 , и на концах этого промежутка принимает значения разных знаков; тогда найдется точка
, и на концах этого промежутка принимает значения разных знаков; тогда найдется точка 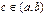 , в которой функция равна нулю.
, в которой функция равна нулю. определена и непрерывна на отрезке
определена и непрерывна на отрезке 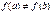 то функция принимает все свои промежуточные значения, принадлежащие промежутку
то функция принимает все свои промежуточные значения, принадлежащие промежутку  , где
, где 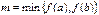 ,
, 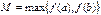 ,
,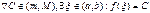 .
. определена и непрерывна на отрезке
определена и непрерывна на отрезке 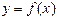 является ограниченной на этом отрезке.
является ограниченной на этом отрезке.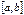 , тогда функция
, тогда функция 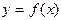 имеет минимум и максимум на этом отрезке (множество значений функции включает в себя точные верхнюю и нижнюю границы).
имеет минимум и максимум на этом отрезке (множество значений функции включает в себя точные верхнюю и нижнюю границы).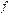 в точке
в точке 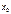 , т.е. выполнение условия (3), означает, что оба односторонних предела
, т.е. выполнение условия (3), означает, что оба односторонних предела 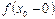 и
и 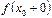 существуют и равны
существуют и равны 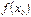 , т.е.
, т.е. 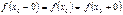
 называют точкой разрыва функции
называют точкой разрыва функции 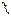 . Условие (4) означает выполнение следующих четырех условий, каждое из которых предполагает выполнение всех предыдущих:
. Условие (4) означает выполнение следующих четырех условий, каждое из которых предполагает выполнение всех предыдущих: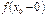 и
и 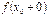 существуют;
существуют; и
и 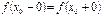 ;
; .
. называют точкой конечного скачка. Величина
называют точкой конечного скачка. Величина  называется скачком функции
называется скачком функции 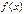 в точке
в точке 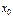 .
.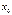 называют точкой устранимого разрыва.
называют точкой устранимого разрыва.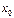 и не определена в самой точке
и не определена в самой точке 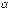 и
и 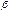 называются бесконечно малыми одного порядка, если предел их отношения есть конечное число, отличное от нуля, т.е.
называются бесконечно малыми одного порядка, если предел их отношения есть конечное число, отличное от нуля, т.е.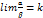 ;
; 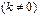
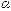 называется бесконечно малой величиной высшего порядка по сравнению с
называется бесконечно малой величиной высшего порядка по сравнению с  , если предел отношения
, если предел отношения  к
к 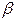 равен нулю, т.е.
равен нулю, т.е. 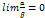 ;
;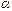 называется бесконечно малой величиной низшего порядка по сравнению с
называется бесконечно малой величиной низшего порядка по сравнению с 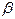 , если предел отношения
, если предел отношения 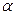 к
к 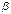 является бесконечно большой величиной, т.е.
является бесконечно большой величиной, т.е. 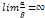 ;
;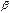 называются эквивалентными бесконечно малыми, если предел их отношения равен единице, т.е.
называются эквивалентными бесконечно малыми, если предел их отношения равен единице, т.е. 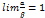 .
.


