Построение гистограммы и графика на нормальной вероятностной бумаге.

Задание на курсовую работу

Даны исходные данные для первой и второй совокупности

Таблица 1

Исходные данные для первой совокупности

Таблица 2

Исходные данные для второй совокупности

1. Используя пакет MathCAD сформировать две обучающих выборки для двух диагностируемых классов. В каждую выборку входит по пять вариационных рядов Х1…Х5 и Х11…Х55. Формирование вариационных рядов осуществляется посредством генератора случайных чисел с нормальным законом распределения.

2. По одномерным гистограммам оценить структуру классов.

3. Провести статистический анализ данных (найти основные статистические параметры рядов).

4. Используя пакет STATISTICA определить функции дискриминации и расстояния Махаланобиса.

5. Провести визуализацию данных при помощи построения двумерных моделей.

6. Оценить информативность признаков, при необходимости удалить неинформативные.

7. Выбрать тип решающего правила.

8. Найти численные значения параметров решающего правила.

9. Используя данные таблиц в качестве контрольной выборки найти значение вероятности правильной классификации полученной модели.

 

Введение

 

Стати́стика — отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических (количественных или качественных) данных.

Слово «статистика» происходит от латинского status — состояние дел. В науку термин «статистика» ввел немецкий ученый Готфрид Ахенваль в 1746 году, предложив заменить название курса «Государствоведение», преподававшегося в университетах Германии, на «Статистику», положив тем самым начало развитию статистики как науки и учебной дисциплины. Несмотря на это, статистический учет вёлся намного раньше: проводились переписи населения в Древнем Китае, осуществлялось сравнение военного потенциала государств, велся учет имущества граждан в Древнем Риме и т. п.

Статистика разрабатывает специальную методологию исследования и обработки материалов: массовые статистические наблюдения, метод группировок, средних величин, индексов, балансовый метод, метод графических изображений и другие методы анализа статистических данных. Статистика – это самостоятельная общественная наука, которая изучает количественную сторону массовых явлений и процессов, исследует закономерности общественного развития в конкретных условиях, места и времени. Статистика изучает статистические закономерности, которые в отличие от динамических проявляются только в массовых процессах.

Теория статистики – наука о наиболее общих принципах и методах статистического исследования социально-экономических явлений. Она разрабатывает понятийный аппарат и систему категорий статистической науки, рассматривает методы сбора, сводки, обобщения и анализа статистических данных, т. е. общую методологию статистического исследования массовых общественных процессов. Таким образом, теория статистики – методологическая основа всех отраслевых статистик.

MathCAD

Система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.

Объединяет в себе простой текстовый редактор, математический интерпретатор и графический процессор. Система ориентирована на IBM - совместимые компьютеры. Упомянутые выше документы содержат текстовые, формульные и графические блоки. На экране дисплея они занимают прямоугольные области, границы которых обычно не видны (но при введении в блок курсора противолежащие углы прямоугольных областей отмечаются прямоугольниками). Блоки выполняются слева направо и сверху вниз.

Подготовка и исполнение документов MathCAD может осуществляется с помощью: главного меню и спускающихся подменю (для их появления необходимо нажать клавишу), командного режима (вводится нажатием клавиши и команд в верхней командной строке), комбинации обычных клавиш, а так же с помощью управляющих клавиш. В последнем случае, например, нажатие клавиши обеспечивает вызов системы подсказок, - загрузку документов с дискового накопителя, - запись редактируемого документа на диск и т.д.

Из режимов работы необходимо особо отметить режимы auto и manual. Режим auto обеспечивает автоматические вычисления сразу после загрузки документа по мере его прокрутки (скроллинга) на экране дисплея. В этом режиме скроллинг ощутимо замедлен, особенно при использовании системы на ПК класса IBM PC XT без математического сопроцессора. Режим manual (ручной) позволяет осуществлять быстрый скроллинг без выполнения документа. Для проведения вычислений от начала документа и до конца видимой на экране дисплея его части нужно нажать клавишу.

Текстовые блоки являются не более чем комментариями. Их назначение - пояснить сухое и лаконичное математическое описание, представленное на входном языке системы. Текстовые блоки могут быть полноформатными (на всю длину строки) и в виде прямоугольников ограниченных размеров. Если ввести знак «кавычки», то на экране дисплея появится пара кавычек, между которыми вводить и редактировать текст в обычном порядке.

Текстовый редактор системы не обладает всеми возможностями специализированных редакторов текста, однако позволяет корректировать тексты, выравнивать их по краю, перемещать текстовые блоки в любое место документа и т.д. Весьма удобны средства редактирования документов, позволяющие, в частности, стирать указанный курсором блок (клавиша) и вставлять блок на новое место (клавиша).

Математические формулы, подлежащие интерпретации, записываются в общепринятом виде. Имеется возможность изменения формата представления чисел, например числа знаков после разделительной точки, погрешности вычислений и обозначения мнимой единицы (i на j и наоборот) при операциях с комплексными числами.

 

 

	X1	X2	X3	X4
	-54		-24
	-37		-27
	-4
	-68
	-9
	-23
	-42
			-58
	-99
	-7
	-1
			-81
	-140
	-65
	-47
	-22

 

	X11	X22	X33	X44
		-40	-35
		-21	-44
		-96	-98
		-14	-16
	-9	-10	-59
		-36	-29
		-21	-55
		-80	-48
			-32
		-60
			-53
		-28
		-66	-48
		-40	-36
		-15
		-40	-22
	-18	-68	-28
			-15
		-163	-1

 

 

Наблюдений).,,

Пересмотра модели

рис.1 График на нормальной вероятностной бумаге X1

 

 

 

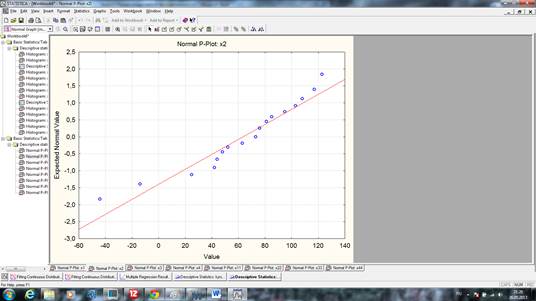
рис.1 График на нормальной вероятностной бумаге X2

 

рис.1 График на нормальной вероятностной бумаге X3

 

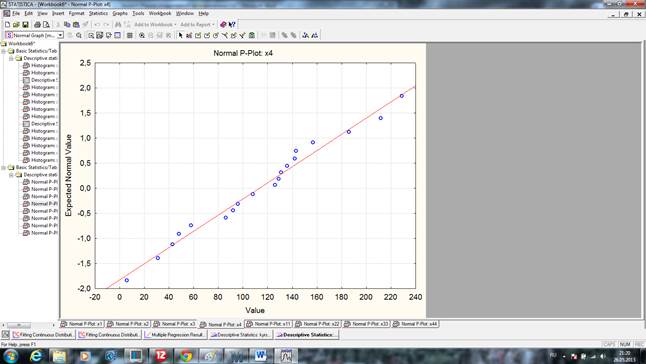
рис.1 График на нормальной вероятностной бумаге X4

 

рис.1 График на нормальной вероятностной бумаге X11

 

рис.1 График на нормальной вероятностной бумаге X22

 

рис.1 График на нормальной вероятностной бумаге X33

 

 

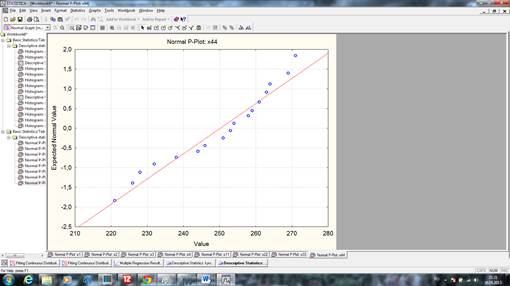
рис.1 График на нормальной вероятностной бумаге X44

 

 

На Рис.4мы видим что происходит отклонение от нормального распределения и данные располагаются волнообразно от прямой нормального распределения, к данным необходимо применить преобразование. График позволяет сделать предположение о недопустимости описания данных с помощью нормального распределения.

 

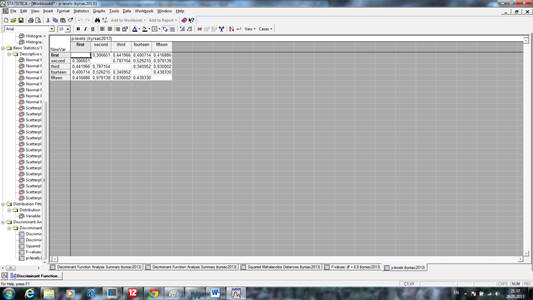
Рис.1 Корреляционная матрица

 

днако роль выбросов для набора независимых переменных часто упускается из виду. Со стороны независимых переменных, имеется список переменных, участвующий с различными весами (регрессионные коэффициенты) в предсказании зависимой переменной. Независимые переменные можно представить себе в виде точек некоторого многомерного пространства, в котором может располагаться каждое наблюдение. Например, если вы имеете две независимые переменные с равными регрессионными коэффициентами, то можно построить диаграмму рассеяния этих двух переменных и расположить каждое наблюдение на этом графике. Вы можете затем нарисовать точку средних значений обоих переменных и вычислить расстояния от каждого наблюдения до этого среднего (называемого теперь центроидом) в этом двумерном пространстве; в этом состоит концептуальная идея, стоящая за вычислением расстояний Махаланобиса. Теперь посмотрим на эти расстояния, отсортированные по величине, с целью идентификации экстремальных наблюдений по независимым переменным. В поле Тип выбросов отметьте опцию расстояний Махаланобиса и нажмите кнопку Построчный график выбросов. Полученный график показывает расстояния Махаланобиса, отсортированные в порядке убывания.

 

В информационной части окна результатов Wilks' Lambda – Значение лямбды Уилкса. Значение лямбды Уилкса лежит в интервал [0, 1]. Значение близкое к 0 говорит о хорошей дискриминации (как в нашем примере

 

Таблица с квадратами расстояния Махаланобиса от точек до центров групп позволяет определить к какой группе относится случай. Случай относится к группе, в до которой расстояние Махаланобиса минимально. Звездочками помечены случаи, классификация которых неверна

 

Задание на курсовую работу

Даны исходные данные для первой и второй совокупности

Таблица 1

Исходные данные для первой совокупности

Таблица 2

Исходные данные для второй совокупности

1. Используя пакет MathCAD сформировать две обучающих выборки для двух диагностируемых классов. В каждую выборку входит по пять вариационных рядов Х1…Х5 и Х11…Х55. Формирование вариационных рядов осуществляется посредством генератора случайных чисел с нормальным законом распределения.

2. По одномерным гистограммам оценить структуру классов.

3. Провести статистический анализ данных (найти основные статистические параметры рядов).

4. Используя пакет STATISTICA определить функции дискриминации и расстояния Махаланобиса.

5. Провести визуализацию данных при помощи построения двумерных моделей.

6. Оценить информативность признаков, при необходимости удалить неинформативные.

7. Выбрать тип решающего правила.

8. Найти численные значения параметров решающего правила.

9. Используя данные таблиц в качестве контрольной выборки найти значение вероятности правильной классификации полученной модели.

 

Введение

 

Стати́стика — отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических (количественных или качественных) данных.

Слово «статистика» происходит от латинского status — состояние дел. В науку термин «статистика» ввел немецкий ученый Готфрид Ахенваль в 1746 году, предложив заменить название курса «Государствоведение», преподававшегося в университетах Германии, на «Статистику», положив тем самым начало развитию статистики как науки и учебной дисциплины. Несмотря на это, статистический учет вёлся намного раньше: проводились переписи населения в Древнем Китае, осуществлялось сравнение военного потенциала государств, велся учет имущества граждан в Древнем Риме и т. п.

Статистика разрабатывает специальную методологию исследования и обработки материалов: массовые статистические наблюдения, метод группировок, средних величин, индексов, балансовый метод, метод графических изображений и другие методы анализа статистических данных. Статистика – это самостоятельная общественная наука, которая изучает количественную сторону массовых явлений и процессов, исследует закономерности общественного развития в конкретных условиях, места и времени. Статистика изучает статистические закономерности, которые в отличие от динамических проявляются только в массовых процессах.

Теория статистики – наука о наиболее общих принципах и методах статистического исследования социально-экономических явлений. Она разрабатывает понятийный аппарат и систему категорий статистической науки, рассматривает методы сбора, сводки, обобщения и анализа статистических данных, т. е. общую методологию статистического исследования массовых общественных процессов. Таким образом, теория статистики – методологическая основа всех отраслевых статистик.

MathCAD

Система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.

Объединяет в себе простой текстовый редактор, математический интерпретатор и графический процессор. Система ориентирована на IBM - совместимые компьютеры. Упомянутые выше документы содержат текстовые, формульные и графические блоки. На экране дисплея они занимают прямоугольные области, границы которых обычно не видны (но при введении в блок курсора противолежащие углы прямоугольных областей отмечаются прямоугольниками). Блоки выполняются слева направо и сверху вниз.

Подготовка и исполнение документов MathCAD может осуществляется с помощью: главного меню и спускающихся подменю (для их появления необходимо нажать клавишу), командного режима (вводится нажатием клавиши и команд в верхней командной строке), комбинации обычных клавиш, а так же с помощью управляющих клавиш. В последнем случае, например, нажатие клавиши обеспечивает вызов системы подсказок, - загрузку документов с дискового накопителя, - запись редактируемого документа на диск и т.д.

Из режимов работы необходимо особо отметить режимы auto и manual. Режим auto обеспечивает автоматические вычисления сразу после загрузки документа по мере его прокрутки (скроллинга) на экране дисплея. В этом режиме скроллинг ощутимо замедлен, особенно при использовании системы на ПК класса IBM PC XT без математического сопроцессора. Режим manual (ручной) позволяет осуществлять быстрый скроллинг без выполнения документа. Для проведения вычислений от начала документа и до конца видимой на экране дисплея его части нужно нажать клавишу.

Текстовые блоки являются не более чем комментариями. Их назначение - пояснить сухое и лаконичное математическое описание, представленное на входном языке системы. Текстовые блоки могут быть полноформатными (на всю длину строки) и в виде прямоугольников ограниченных размеров. Если ввести знак «кавычки», то на экране дисплея появится пара кавычек, между которыми вводить и редактировать текст в обычном порядке.

Текстовый редактор системы не обладает всеми возможностями специализированных редакторов текста, однако позволяет корректировать тексты, выравнивать их по краю, перемещать текстовые блоки в любое место документа и т.д. Весьма удобны средства редактирования документов, позволяющие, в частности, стирать указанный курсором блок (клавиша) и вставлять блок на новое место (клавиша).

Математические формулы, подлежащие интерпретации, записываются в общепринятом виде. Имеется возможность изменения формата представления чисел, например числа знаков после разделительной точки, погрешности вычислений и обозначения мнимой единицы (i на j и наоборот) при операциях с комплексными числами.

 

 

	X1	X2	X3	X4
	-54		-24
	-37		-27
	-4
	-68
	-9
	-23
	-42
			-58
	-99
	-7
	-1
			-81
	-140
	-65
	-47
	-22

 

	X11	X22	X33	X44
		-40	-35
		-21	-44
		-96	-98
		-14	-16
	-9	-10	-59
		-36	-29
		-21	-55
		-80	-48
			-32
		-60
			-53
		-28
		-66	-48
		-40	-36
		-15
		-40	-22
	-18	-68	-28
			-15
		-163	-1

 

 

Построение гистограммы и графика на нормальной вероятностной бумаге.

Представим распределение полученных данных на гистограмме. Для этого предназначена кнопка Histograms окна Descriptive statistics.

Гистограмма используется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений, при этом, генерируются числа попаданий для заданного диапазона.

На гистограмму нанесем кривую плотности нормального распределения, чтобы сделать предположение о виде закона распределения и проверить близость распределения

к нормальному.

рис.1 Одномерная гистограмма вариационного ряда X1

 

рис.1 Одномерная гистограмма вариационного ряда X2

 

 

 

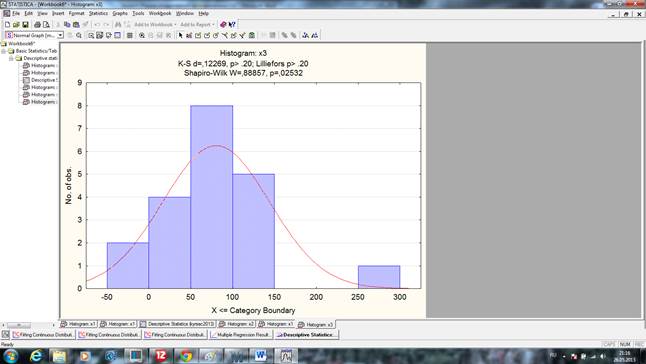
рис.1 Одномерная гистограмма вариационного ряда X3

 

 

рис.1 Одномерная гистограмма вариационного ряда X4

 

рис.1 Одномерная гистограмма вариационного ряда X11

 

рис.1 Одномерная гистограмма вариационного ряда X22

 

рис.1 Одномерная гистограмма вариационного ряда X33

 

рис.1 Одномерная гистограмма вариационного ряда X44

 

На гистограммах показана кривая плотности нормального распределения для первого диагностируемого класса, а также критерий Колмогорова-Смирнова (d). Статистика Колмогорова-Смирнова оказалась равной для X1=0,09, X2=0.07, X3=0.12, X4=0.08, X5=0.05. Чем меньше величина этой статистики, тем ближе распределение случайной величины к нормальному. Вероятность нулевой гипотезы (р) более 0,20.

Отсюда можно выдвинуть нулевую гипотезу о том, что различие между генеральными совокупностями равно нулю, т. е. различие можно объяснить только случайностью выборки.

Теперь посмотрим на гистограммы для второго диагностируемого класса.

 

 

На гистограммах показана кривая плотности нормального распределения для второго диагностируемого класса, а также критерий Колмогорова-Смирнова (d). Статистика Колмогорова-Смирнова оказалась равной для X11=0,12, X22=0.09, X33=0.09, X44=0.07, X5=0.08. Чем меньше величина этой статистики, тем ближе распределение случайной величины к нормальному. Вероятность нулевой гипотезы (р) более 0,20.

Отсюда можно выдвинуть нулевую гипотезу о том, что различие между генеральными совокупностями равно нулю, т. е. различие можно объяснить только случайностью выборки.