Определение основных статистических показателей.

Определим основные статистические характеристики:

Mean – средняя арифметическая. Среднее значение случайной величины представляет собой наиболее типичное, наиболее вероятное её значение, своеобразный центр, вокруг которого разбросаны все значения признака.

Median – медиана – это такое значение случайной величины, которое разделяет все случаи выборки на две равные по численности части, попадания в которые имеют равные вероятности. Геометрический смысл: выборочной медианой называется значение аргумента, которое делит гистограмму плотности вероятности на две равные части.

Minimum, maximum - минимальное и максимальное значения;

Standart Deviation – стандартное отклонение (или среднее квадратичное отклонение), является мерой изменчивости признака. Оно показывает на какую величину в среднем отклоняются случаи от среднего значения признака. Особенно большое значение имеет при исследовании нормальных распределений.

Сoefficient of variation (Коэффициент вариации) — это отношение среднего квадратического отклонения к средней арифметической, выраженное в процентах. Он применяется для сравнений колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим.

Коэффициент вариации используют не только для сравнительной оценки единиц совокупности, но и также для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.

Skewness – асимметрия, характеризует степень смещения вариационного ряда относительно среднего значения по величине и направлению. В симметричной кривой коэффициент асимметрии равен нулю. Если правая ветвь кривой, начиная от вершины, больше левой, то правосторонняя асимметрия и коэффициент асимметрии больше нуля. Левосторонняя асимметрия – наоборот, тогда коэффициент асимметрии меньше нуля. Асимметрия менее 0.5 считается малой

Kurtosis – эксцесс, характеризует степень концентрации случаев вокруг среднего значения и является своеобразной мерой крутости кривой. В кривой нормального распределения эксцесс равен нулю. Если эксцесс больше нуля, то кривая распределения характеризуется островершинностью, т.е. является более крутой по сравнению с нормальной. При отрицательном эксцессе кривая является более плосковершинной, т.е. более пологой по сравнению с нормальным распределением. Отрицательным пределом величины эксцесса является число -2, положительного предела - нет.

Из полученных данных рис.11 и рис.12 можно сказать следующее:

- ассиметрия лежит в диапазоне [-0.6;0.6], что говорит о симметричности графиков и незначительной ассиметрии;

- эксцесс для первого класса в основном больше 0, следовательно вершина графика более острая, чем у графика нормального распределения. А для второго класса ниже 0, что говорит о плосковершинности графика.

- Использование коэффициента вариации имеет смысл при изучении вариации признака, принимающего только положительные значения, тем не менее по полученным данным можно сказать о неоднородности выборок.

- Из стандартного отклонения видно, что наиболее сильной изменчивости подвержены признаки данных 1-го диагностируемого класса, а именно Х1,Х2,Х4.

О нормальности распределения можно судить по графику на нормаль-

Ной вероятностой бумаге. Его легко построить при помощи опции Normal

probability plots окна "Descriptive statistics" (рис.4). Чем ближе распределение к

нормальному виду, тем лучше значения ложатся на прямую линию (рис. 7).

Этот метод оценки является фактически глазомерным. В сомнительных случаях

Проверку на нормальность можно продолжить с использованием специальных

Статистических критериев (Колмогорова-Смирнова, Омега-квадрат (w

)). Одна-

Ко детальная проверка гипотезы о нормальности выборки требует довольно

Значительных объемов выборки (по мнению некоторых авторов не менее 100

Наблюдений).,,

Чем ближе распределение к нормальному виду, тем лучше

Значения остатков ложатся на прямую линию. Важно просмотреть графики зависимости остаток от каждой из незави-

Симых переменных. Остатки должны быть нормально распределены, т.е.

На графике они должны представлять приблизительно горизонтальную полосу

Одинаковой ширины на всем ее протяжении. Коэффициент корреляции (r) меж-

ду регрессионными остатками и переменными должен равняться нулю. В нашем случае на графиках остатков (рис. 42) хорошо просматривается

Нелинейный тренд, что вызывает сомнение в адекватности модели. Присутст-

Вие нелинейного тренда в регрессионных остатках говорит о необходимости

Пересмотра модели

рис.1 График на нормальной вероятностной бумаге X1

 

 

 

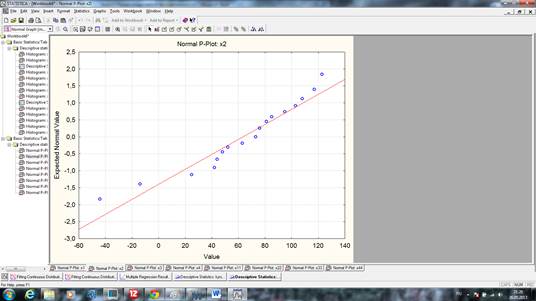
рис.1 График на нормальной вероятностной бумаге X2

 

рис.1 График на нормальной вероятностной бумаге X3

 

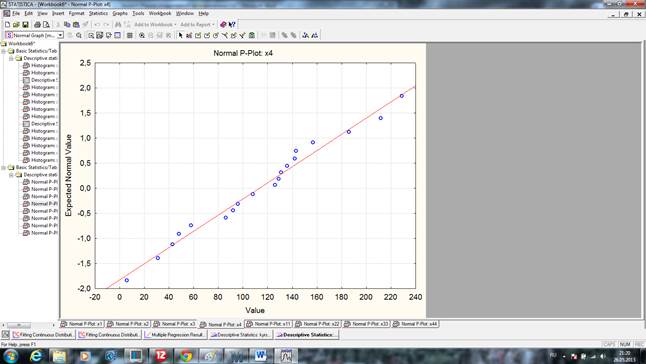
рис.1 График на нормальной вероятностной бумаге X4

 

рис.1 График на нормальной вероятностной бумаге X11

 

рис.1 График на нормальной вероятностной бумаге X22

 

рис.1 График на нормальной вероятностной бумаге X33

 

 

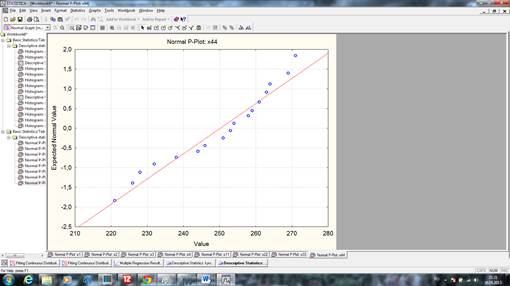
рис.1 График на нормальной вероятностной бумаге X44

 

 

На Рис.4мы видим что происходит отклонение от нормального распределения и данные располагаются волнообразно от прямой нормального распределения, к данным необходимо применить преобразование. График позволяет сделать предположение о недопустимости описания данных с помощью нормального распределения.

 

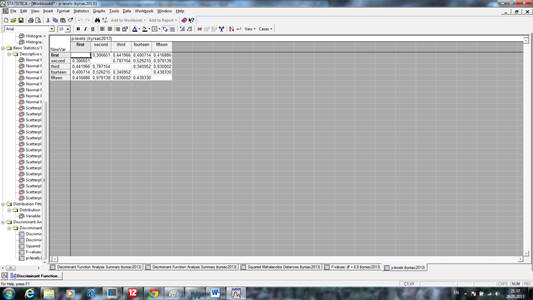
Рис.1 Корреляционная матрица

 

днако роль выбросов для набора независимых переменных часто упускается из виду. Со стороны независимых переменных, имеется список переменных, участвующий с различными весами (регрессионные коэффициенты) в предсказании зависимой переменной. Независимые переменные можно представить себе в виде точек некоторого многомерного пространства, в котором может располагаться каждое наблюдение. Например, если вы имеете две независимые переменные с равными регрессионными коэффициентами, то можно построить диаграмму рассеяния этих двух переменных и расположить каждое наблюдение на этом графике. Вы можете затем нарисовать точку средних значений обоих переменных и вычислить расстояния от каждого наблюдения до этого среднего (называемого теперь центроидом) в этом двумерном пространстве; в этом состоит концептуальная идея, стоящая за вычислением расстояний Махаланобиса. Теперь посмотрим на эти расстояния, отсортированные по величине, с целью идентификации экстремальных наблюдений по независимым переменным. В поле Тип выбросов отметьте опцию расстояний Махаланобиса и нажмите кнопку Построчный график выбросов. Полученный график показывает расстояния Махаланобиса, отсортированные в порядке убывания.

 

В информационной части окна результатов Wilks' Lambda – Значение лямбды Уилкса. Значение лямбды Уилкса лежит в интервал [0, 1]. Значение близкое к 0 говорит о хорошей дискриминации (как в нашем примере

 

Таблица с квадратами расстояния Махаланобиса от точек до центров групп позволяет определить к какой группе относится случай. Случай относится к группе, в до которой расстояние Махаланобиса минимально. Звездочками помечены случаи, классификация которых неверна