
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная зависимость и независимость строк матрицыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Введем понятие линейной зависимости и независимости строк матрицы. Пусть дана некоторая матрица А =
где
или Из (3.3.1) вытекает, что
где Определение. Строки
Если равенство (3.3.3) справедливо тогда и только тогда, когда Легко видеть и обратное: если строки линейно зависимы, то найдется строка, которая будет линейной комбинацией остальных строк. Пусть, например, в (3.3.3) Определение. Пусть в матрице А выделен некоторый минор r -го порядка Теперь докажем важную лемму. Лемма об окаймляющих минорах. Если минор Доказательство. Не нарушая общности рассуждений, будем считать, что отличный от нуля минор r -го порядка
Для первых k строк матрицы А утверждение леммы очевидно: достаточно в линейную комбинацию включить эту же строку с коэффициентом, равным единице, а остальные – с коэффициентами, равными нулю. Докажем теперь, что и остальные строки матрицы А линейно выражаются через первые k строк. Для этого построим минор (r +1)-го порядка
Полученный минор равен нулю при всех k и l. Если
Разложим минор
где
где Полагая
Выражение (3.3.6) означает, что k -я строка матрицы А линейно выражается через первые r строк. Так как при транспонировании матрицы значения ее миноров не изменяются (ввиду свойства определителей), то все доказанное справедливо и для столбцов. Теорема доказана. Следствие I. Любая строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов). Действительно, базисный минор матрицы отличен от нуля, а все окаймляющие его миноры равны нулю. Следствие II. Определитель n -го порядка тогда и только тогда равен нулю, когда он содержит линейно зависимые строки (столбцы). Достаточность линейной зависимости строк (столбцов) для равенства определителя нулю доказана ранее как свойство определителей. Докажем необходимость. Пусть задана квадратная матрица n -го порядка, единственный минор которой Докажем еще одну теорему о ранге матрицы. Теорема. Максимальное число линейно независимых строк матрицы равно максимальному числу ее линейно независимых столбцов и равно рангу этой матрицы. Доказательство. Пусть ранг матрицы А = В заключение изложим еще один метод нахождения ранга матрицы. Ранг матрицы можно определить, если найти минор максимального порядка, отличный от нуля. На первый взгляд, это требует вычисления хотя и конечного, но быть может, очень большого числа миноров этой матрицы. Следующая теорема позволяет, однако, внести в этот значительные упрощения.
Теорема. Если минор Доказательство. Достаточно показать, что любая подсистема строк матрицы Предположим противное. Пусть строки
Рассмотрим матрицу К из коэффициентов линейных выражений (3.3.7):
Строки этой матрицы обозначим через
Перейдем к равенству компонент
Теперь рассмотрим следующую линейную комбинацию:
Используя (3.3.7) и (3.3.8), получаем
что противоречит линейной независимости строк Следовательно, наше предположение неверно и, значит, любые S>r строк в условиях теоремы линейно зависимы. Теорема доказана. Рассмотрим правило вычисления ранга матрицы – метод окаймляющих миноров, основанный на данной теореме. При вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если уже найден минор r-го порядка Пример. Вычислить методом окаймляющих миноров ранг матрицы
Решение. Минор второго порядка, стоящий в левом верхнем углу матрицы А, отличен от нуля:
Однако все окаймляющие его миноры третьего порядка равны нулю:
Следовательно, ранг матрицы А равен двум: Первая и вторая строки, первый и второй столбцы в данной матрице являются базисными. Остальные строки и столбцы являются их линейными комбинациями. В самом деле, для строк справедливы следующие равенства:
В заключение отметим справедливость следующих свойств: 1) ранг произведения матриц не больше ранга каждого из сомножителей; 2) ранг произведения произвольной матрицы А справа или слева на невырожденную квадратную матрицу Q равен рангу матрицы А. Многочленные матрицы
Определение. Многочленной матрицей или Над 1. перестановка двух строк (столбцов); 2. умножение строки (столбца) на число, отличное от нуля; 3. прибавление к одной строке (столбцу) другой строки (столбца), умноженной на любой многочлен Две Пример. Доказать эквивалентность матриц
Решение. 1. Поменяем местами в матрице
2. Из второй строки вычтем первую, умноженную на (
3. Умножим вторую строку на (–1) и заметим, что
Получим
4. Вычтем из второго столбца первый, умноженный на
Множество всех Каждый класс эквивалентных матриц характеризуется канонической, или нормальной, Определение. Канонической, или нормальной, Из определения следует, что если среди многочленов имеются многочлены нулевой степени, то они в начале главной диагонали. Если имеются нули, то они стоят в конце главной диагонали. Матрица
также каноническая. Каждый класс Многочлены, стоящие на главной диагонали канонической формы данной Один из методов вычисления инвариантных множителей состоит в приведении данной Так, для матрицы
Из сказанного следует, что наличие одной и той же совокупности инвариантных множителей является необходимым и достаточным условием эквивалентности Приведение
где r – ранг Пример. Пусть дана
Решение. Очевидно, наибольший общий делитель первого порядка D1 =1, т.е. Определим миноры второго порядка:
Уже этих данных достаточно для того, чтобы сделать вывод: D2 =1, следовательно, Определяем D3
Следовательно, Таким образом, канонической формой данной матрицы является следующая
Матричным многочленом называется выражение вида
где
Если Любую квадратичную Справедливость данных утверждений со всей очевидностью вытекает из свойств операций над матрицами. Остановимся на следующих примерах: Пример. Представить многочленную матрицу
в виде матричного многочлена можно следующим образом
Пример. Матричный многочлен
можно представить в виде следующей многочленной матрицы (
Эта взаимозаменяемость матричных многочленов и многочленных матриц играет существенную роль в математическом аппарате методов факторного и компонентного анализа. Матричные многочлены одинакового порядка можно складывать, вычитать и умножать аналогично обычным многочленам с числовыми коэффициентами. Следует, однако, помнить, что умножение матричных многочленов, вообще говоря, не коммутативно, т.к. не коммутативно умножение матриц. Два матричных многочлена называются равными, если равны их коэффициенты, т.е. соответствующие матрицы при одинаковых степенях переменного Суммой (разностью) двух матричных многочленов Чтобы умножить матричный многочлен Степень матричного многочлена – произведения Операции над матричными многочленами можно осуществлять с помощью операций над соответствующими Чтобы сложить (вычесть) матричные многочлены, достаточно сложить (вычесть) соответствующие Пример.
С другой стороны
Так как умножение матриц не коммутативно, для матричных многочленов определяются два деления с остатком – правое и левое. Пусть даны два матричных многочлена порядка n
где В 0 – невырожденная матрица. При делении
где степень R1 меньше степени
где степень Обобщённая теорема Безу. При делении матричного многочлена
а левый остаток – левому значению делимого
Доказательство. Доказательство справедливости обеих формул (3.4.1) и (3.4.2) осуществляется одинаково, непосредственной подстановкой. Докажем одну из них.
Итак, делимое –
Определим произведение
т.е. или т.е. что и требовалось доказать. Следствие. Пример. Показать, что матричный многочлен
делится на матричный многочлен где Решение. В самом деле, справедливо равенство
Подсчитаем значение левого остатка по теореме Безу
3.5. Задания для самостоятельной работы по главе 3 3.1. Найти обратную матрицу
3.2. Найти обратную матрицу порядка n
3.3. Найти обратную матрицу порядка n
3.4. Найти обратную матрицу порядка n
3.5. Найти обратную матрицу
3.6. Найти обратную матрицу порядка (n+1)
3.7. Найти обратную матрицу порядка n
3.8. Как изменится обратная матрица а) переставить i -ую и j -ую строки? б) i -ую строку умножить на число с, не равное нулю? в) к i -ой строке прибавить j -ую, умноженную на число с, или совершить аналогичное преобразование столбцов?
3.9. Найти матрицу
3.10. Показать, что операция транспонирования матрицы обладает свойствами: а) б) в) г) где с – число, а А и В – матрицы.
3.11. Доказать, что если А и В – симметрические квадратные матрицы одинакового порядка, то матрица
3.12. Показать, что для любой матрицы В матрица
3.13. Квадратная матрица а) столбцы А образуют ортонормированную систему, т.е.
где б) строки А образуют ортонормированную систему, т.е.
3.14. Доказать, что ранг суммы двух матриц не больше суммы их рангов.
3.15. Доказать, что если ранг матрицы А равен r, то минор d, стоящий на пересечении любых r линейно независимых строк и r линейно независимых столбцов этой матрицы, отличен от нуля.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1106; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.29.183 (0.015 с.) |

 и
и  ее строки. Будем говорить, что k -ая (
ее строки. Будем говорить, что k -ая ( ) строка матрицы является линейной комбинацией остальных ее строк (линейно выражается через остальные), если
) строка матрицы является линейной комбинацией остальных ее строк (линейно выражается через остальные), если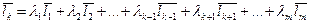
 – какие-то числа (некоторые из этих чисел или даже все могут быть равны нулю). Это означает наличие следующих равенств между элементами столбцов:
– какие-то числа (некоторые из этих чисел или даже все могут быть равны нулю). Это означает наличие следующих равенств между элементами столбцов:
 ,
,  .
. ,
,
 – нулевая строка.
– нулевая строка. , не все равные нулю одновременно, что
, не все равные нулю одновременно, что
 , то строки
, то строки  , тогда
, тогда  .
. и пусть минор (r +1)-го порядка этой же матрицы
и пусть минор (r +1)-го порядка этой же матрицы  целиком содержит внутри себя минор
целиком содержит внутри себя минор  .
.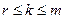 ) и l -го столбца (
) и l -го столбца ( ):
): .
. , то он равен нулю как содержащий два одинаковых столбца. Если
, то он равен нулю как содержащий два одинаковых столбца. Если  , то полученный минор
, то полученный минор 
 – алгебраические дополнения к элементам
– алгебраические дополнения к элементам  . Алгебраические дополнение
. Алгебраические дополнение 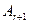 есть минор
есть минор  . Разделим (3.3.4) на
. Разделим (3.3.4) на 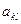 через
через  :
:
 ,
, 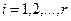 .
. , получим:
, получим:
 равен нулю. Отсюда следует, что ранг этой матрицы меньше n, т.е. найдется хотя бы одна строка, которая является линейной комбинацией базисных строк этой матрицы.
равен нулю. Отсюда следует, что ранг этой матрицы меньше n, т.е. найдется хотя бы одна строка, которая является линейной комбинацией базисных строк этой матрицы. при S>r будет в условиях теоремы линейно зависимой (отсюда будет следовать, что r – максимальное число линейно независимых строк матрицы или любые ее миноры порядка больше чем k равны нулю).
при S>r будет в условиях теоремы линейно зависимой (отсюда будет следовать, что r – максимальное число линейно независимых строк матрицы или любые ее миноры порядка больше чем k равны нулю). , в которых стоит минор
, в которых стоит минор 
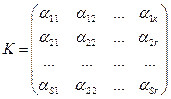 .
.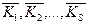 . Они будут линейно зависимы, так как ранг матрицы К, т.е. максимальное число ее линейно независимых строк, не превышает r<S. Поэтому существуют такие числа
. Они будут линейно зависимы, так как ранг матрицы К, т.е. максимальное число ее линейно независимых строк, не превышает r<S. Поэтому существуют такие числа  , не все равны нулю, что
, не все равны нулю, что .
. ,
,  .
.
 или
или 
 ,
, .
.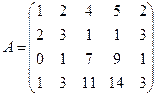 .
.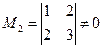 .
. ;
;
 ;
;
 ;
;
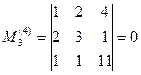 ;
;
 ;
;
 .
.
 .
.
 -матрицей называется прямоугольная матрица, элементы которой являются многочленами от одного переменного
-матрицей называется прямоугольная матрица, элементы которой являются многочленами от одного переменного  .
. и
и  одинаковых размеров называются эквивалентными:
одинаковых размеров называются эквивалентными:  , если от матрицы
, если от матрицы  ,
,
 .
.
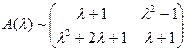 .
. ):
): .
. .
. .
. , получим
, получим .
. разбивается на непересекающиеся классы эквивалентных матриц. Матрицы, эквивалентные между собой, образуют один класс, не эквивалентные – другой.
разбивается на непересекающиеся классы эквивалентных матриц. Матрицы, эквивалентные между собой, образуют один класс, не эквивалентные – другой. называется
называется  , где р – меньшее из чисел m и n (
, где р – меньшее из чисел m и n ( ), причем не равные нулю многочлены имеют старшие коэффициенты, равные 1, и каждый следующий многочлен делиться на предыдущий. Все элементы вне главной диагонали равны 0.
), причем не равные нулю многочлены имеют старшие коэффициенты, равные 1, и каждый следующий многочлен делиться на предыдущий. Все элементы вне главной диагонали равны 0.
 предыдущего примера инвариантными множителями являются
предыдущего примера инвариантными множителями являются ,
,  ,
,  ,
,  .
. -матриц.
-матриц. ,
,  ;
; 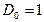 ,
, – наибольший общий делитель миноров k -го порядка, взятый со старшим коэффициентом, равным 1.
– наибольший общий делитель миноров k -го порядка, взятый со старшим коэффициентом, равным 1. .
.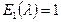 .
. ,
,

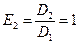 .
. ,
, .
. .
. ,
, – квадратные матрицы порядка n с числовыми элементами.
– квадратные матрицы порядка n с числовыми элементами. , то S называют степенью матричного многочлена, n – порядком матричного многочлена.
, то S называют степенью матричного многочлена, n – порядком матричного многочлена.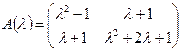
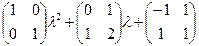 .
.
 .
.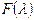 и
и  называется такой матричный многочлен, у которого коэффициент при каждой степени переменного
называется такой матричный многочлен, у которого коэффициент при каждой степени переменного 
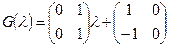


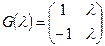
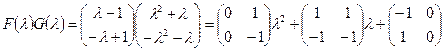


 и правый остаток
и правый остаток 
 ,
, (деление без остатка), а также левое частное
(деление без остатка), а также левое частное  и левый остаток
и левый остаток 

 правый остаток равен правому значению делимого
правый остаток равен правому значению делимого  , т.е. матрице
, т.е. матрице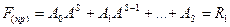 ,
,
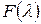 при
при 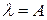 , т.е. матрице
, т.е. матрице
 , делитель –
, делитель –  , в качестве частного имеем многочлен
, в качестве частного имеем многочлен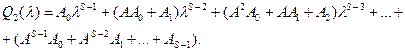
 :
:



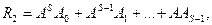
 равно 0.
равно 0.
 , слева без остатка.
, слева без остатка. , где
, где 
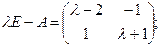


 .
.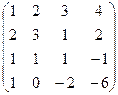 .
. .
. .
.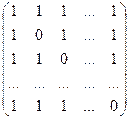 .
.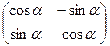 .
. .
. .
. , если в данной матрице
, если в данной матрице  :
: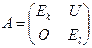 , где
, где  и
и  – единичные матрицы соответственно порядков k и l, U – произвольная матрица порядка
– единичные матрицы соответственно порядков k и l, U – произвольная матрица порядка 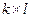 , а все остальные элементы равны нулю.
, а все остальные элементы равны нулю. ;
; ;
; ;
; ,
, является симметрической.
является симметрической. является симметрической.
является симметрической. порядка n называется ортогональной, если
порядка n называется ортогональной, если  , где Е – единичная матрица. Показать, что для ортогональности квадратной матрицы А необходимо и достаточно любое из следующих условий:
, где Е – единичная матрица. Показать, что для ортогональности квадратной матрицы А необходимо и достаточно любое из следующих условий: ,
, – символ Кронекера, обозначающий 1 при i=j и 0 при
– символ Кронекера, обозначающий 1 при i=j и 0 при  ;
; .
.


