
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однородные системы линейных уравненийСодержание книги
Поиск на нашем сайте Однородной называется система линейных уравнений, свободные члены которой равны нулю:
Очевидно, что система однородных уравнений (4.5.1) всегда совместна, так как имеет нулевое решение Это следует также из теоремы Кронекера-Капелли: в случае однородной системы При решении системы однородных уравнений можно поставить вопрос: при каком условии однородная система (4.5.1) является неопределенной, т.е. имеет ненулевые решения. Ответ на этот вопрос дает следующая теорема. Теорема. Для того чтобы система (4.5.1) имеет ненулевые решения, необходимо и достаточно, чтобы выполнялось условие Действительно, если Пусть
Итак, любая линейная комбинация решений однородной системы (4.5.1) тоже будет ее решением. Определение. Линейно независимая система решений Теорема. Если Доказательство. Пусть
Придавая свободным неизвестным значения
Решения Покажем теперь, что каждое решение системы (4.5.1) линейно выражаются через
Очевидно, что все элементы, начиная с k -ого элемента, в решении Рассмотрим систему уравнений
и соответствующую ей систему однородных уравнений
Пусть
будет решением системы (4.5.4), и если
является решением системы (4.5.3). Отсюда следует, что все решения системы (4.5.3) можно получить, прибавляя к одному какому-нибудь ее решению всевозможные решения однородной системы (4.5.4). Таким образом, общее решение системы (4.5.3) равно линейной комбинации общего решения однородной системы (4.5.4) и произвольного, но фиксированного решения системы (4.5.3). Если Пример. Найти фундаментальную систему однородной системы уравнений
Решение. Решаем систему методом Жордана-Гаусса:
Общее решение имеет вид: Решение
и решение
Таким образом, одна из фундаментальных систем решений имеет вид:
Общее решение системы можно представить в следующем виде:
где
4.6. Задания для самостоятельной работы по главе 4
4.1. Решить систему линейных уравнений по правилу Крамера.
4.2. Решить систему линейных уравнений по правилу Крамера.
4.3. Решить систему линейных уравнений по правилу Крамера.
4.4. Решить систему линейных уравнений по правилу Крамера.
4.5. Решить систему линейных уравнений по правилу Крамера.
4.6. Решить систему линейных уравнений методом Жордана-Гаусса.
4.7. Решить систему линейных уравнений методом Жордана-Гаусса.
4.8. Решить систему линейных уравнений методом Жордана-Гаусса.
4.9. Решить систему линейных уравнений методом Жордана-Гаусса.
4.10. Решить систему линейных уравнений методом Жордана-Гаусса.
4.11. Исследовать совместимость и найти общее и одно базисное решение системы линейных уравнений.
4.12. Исследовать совместимость и найти общее и одно базисное решение системы линейных уравнений.
4.13. Исследовать систему и найти общее решение в зависимости от значения параметра
4.14. Найти общее решение и фундаментальную систему решений для однородной системы уравнений.
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |


 .
.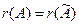 .
. .
. , то система имеет единственное и, значит, только нулевое решение:
, то система имеет единственное и, значит, только нулевое решение:  – какое-нибудь ненулевое решение однородной системы (4.5.1). Представим это решение как вектор-строку
– какое-нибудь ненулевое решение однородной системы (4.5.1). Представим это решение как вектор-строку  . Тогда
. Тогда 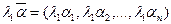 тоже, очевидно, будет решением системы (4.5.1). Далее, если
тоже, очевидно, будет решением системы (4.5.1). Далее, если 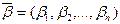 какое-то другое решение системы (4.5.1), отличное от
какое-то другое решение системы (4.5.1), отличное от 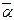 , то при любых
, то при любых  линейная комбинация
линейная комбинация  данных решений тоже будет решением системы, так как если
данных решений тоже будет решением системы, так как если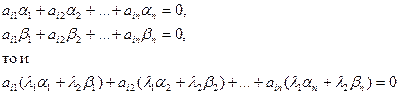
 системы (4.5.1) называется фундаментальной, если каждое решение системы (4.5.1) является линейной комбинацией решений
системы (4.5.1) называется фундаментальной, если каждое решение системы (4.5.1) является линейной комбинацией решений  .
. первых r уравнений системы (4.6.1) в правые части, получим систему
первых r уравнений системы (4.6.1) в правые части, получим систему
 , получим соответствующие значения
, получим соответствующие значения  первых r неизвестных. Аналогично, придавая свободным неизвестным значения
первых r неизвестных. Аналогично, придавая свободным неизвестным значения 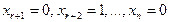 , получим:
, получим:  и т.д. В результате будет найдено k=n-r решений системы (4.5.1):
и т.д. В результате будет найдено k=n-r решений системы (4.5.1):
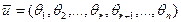 – произвольное решение системы (4.5.1). Составим новое решение
– произвольное решение системы (4.5.1). Составим новое решение 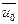 как следующую линейную комбинацию решений
как следующую линейную комбинацию решений 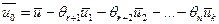
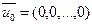 и тогда
и тогда  , т.е. произвольное решение
, т.е. произвольное решение 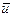 является линейной комбинацией линейно независимых решений
является линейной комбинацией линейно независимых решений 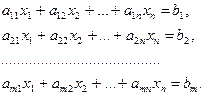
 – какое-то решение системы (4.5.3) и
– какое-то решение системы (4.5.3) и  любое другое ее решение, отличное от
любое другое ее решение, отличное от  . Очевидно, что разность
. Очевидно, что разность
 – произвольное решение однородной системы (4.5.4), то очевидно, что
– произвольное решение однородной системы (4.5.4), то очевидно, что
 , где
, где 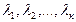 – произвольные числа.
– произвольные числа.

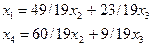 .
. :
: ,
, получим, полагая
получим, полагая  :
: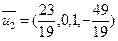 .
.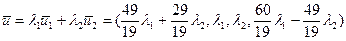 ,
, – произвольные числа. Например, полагая
– произвольные числа. Например, полагая  , получим одно из частных решений:
, получим одно из частных решений:  .
.
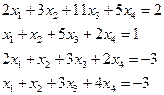
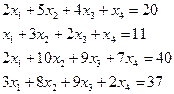

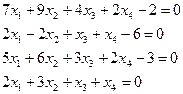

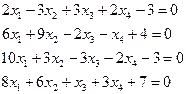


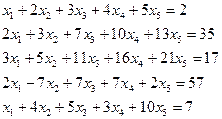
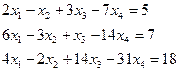
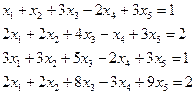
 .
.



