
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 4. Решение системы линейных уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Система линейных уравнений Системой m линейных уравнений с n неизвестными называется система m алгебраических уравнений первой степени вида
где
Решением системы уравнений (4.1.1) называется совокупность n чисел Если система линейных уравнений (4.1.1) имеет хотя бы одно решение, то она называется совместной. В противном случае система называется несовместной. Совместная система, имеющая единственное решение, называется определенной, а система, имеющая более одного решения – неопределенной. Две системы линейных уравнений называются эквивалентными, если любое решение каждой из них является одновременно решением и другой системы. Две произвольные несовместные системы считаются эквивалентными. Системе линейных уравнений (4.1.1) поставим в соответствие матрицу
полученную присоединением к матрице А столбца свободных членов.
Методы решения системы n линейных уравнений с n неизвестными
Рассмотрим систему n линейных уравнений с n неизвестными
Определитель | A | матрицы А называется определителем системы (4.2.1). Теорема Крамера. Если определитель | A | системы (4.2.1) отличен от нуля, то система совместна и имеет единственное решение. Доказательство. Пусть система (4.2.1) совместна и
Умножим обе части первого из равенств (4.2.2) на алгебраическое дополнение
Коэффициент при Обозначим данный определитель через
Тогда равенство (4.2.3) примет вид:
Из формулы (4.2.4) следует, что если система (4.2.1) совместна, то она обладает единственным решением.
Формулы (4.2.4) называются формулами Крамера. Непосредственной подстановкой значений
При Таким образом, получим
Теорема доказана. Пример. Решить систему линейных уравнений методом Крамера:
Решение. Вычислим определитель
откуда Решение системы линейных уравнений с определителем | A |, отличным от нуля, можно найти с помощью обратной матрицы. Для этого запишем систему (4.2.1) в виде матричного уравнения
где Решение матричного уравнения (4.2.5) имеет вид
Пример. Решить систему линейных уравнений с помощью обратной матрицы
Решение. Вычислим для матрицы
ее обратную матрицу
Определим неизвестную матрицу-столбец Х:
откуда Формулы Крамера (4.2.4) могут быть получены из выражения (4.2.6). Действительно, запишем матричное равенство
Из полученного выражения непосредственно следуют формулы Крамера:
Теорема Кронекера-Карелли Теорема. Система линейных уравнений (4.1.1) совместна тогда и только тогда, когда Доказательство. Необходимость. Пусть система (4.1.1) совместна и пусть числа Достаточность. Пусть дано, что
откуда следует, что числа На основании теоремы Кронекера-Капелли имеем: 1. Если
2. Если Пусть для определенности базисный минор порядка r расположен в верхнем левом углу матрицы А. Тогда первые r строк матрицы А линейно независимы, а остальные ее строки являются линейной комбинацией первых r строк. Но это означает, что первые r уравнений системы (4.1.1) линейно независимы, а остальные (m-r) ее уравнений являются их линейными комбинациями. Поэтому достаточно решить систему r уравнений; решения такой системы будут, очевидно, удовлетворять и остальным (m-r) уравнениям. При этом возможны два случая: 1.
можно решить, например, по правилу Крамера. В этом случае система имеет единственное решение, т.е. система совместна и определена; 2.
Очевидно, что полученная система и, следовательно, система (4.1.1) являются совместными и неопределенными. Таким образом, если Если в системе n линейных уравнений с n неизвестными определитель системы равен нулю, то Теорема Кронекера-Капелли устанавливает необходимое и достаточное условие совместности системы (4.1.1), но не дает способа нахождения решения этой системы. Рассмотрим метод Жордана-Гаусса – метод решения системы m линейных уравнений с n неизвестными.
Метод Жордана-Гаусса
Метод Жордана-Гаусса основан на элементарных преобразованиях (п.3.2) строк расширенной матрицы
системы (4.1.1). В результате каждого из элементарных преобразований расширенная матрица изменяется, однако системы линейных уравнений, соответствующие полученным матрицам, эквивалентны исходной системе линейных уравнений. Пусть дана система m линейных уравнений с n неизвестными. Применяя элементарные преобразования, построим эквивалентную систему специального вида. Для этого выберем в качестве первого уравнений одно из тех уравнений системы, где коэффициент при х 1 отличен от нуля. Не нарушая общности, предположим, что
Умножим первое уравнение на
Может случиться, что на первом шаге вместе с неизвестными х 1 будут исключены неизвестными
Используем второе уравнение для исключения неизвестного
Продолжая процесс, после r шагов получим матрицу При этом возможны три случая: 1. Если
Система имеет единственное решение:
2. Если
Система имеет бесконечное множество решений. Общее решение имеет вид:
Неизвестные Свободным неизвестным Среди частных решений системы выделим базисные решения, которые получают при равенстве нулю всех свободных неизвестных. Очевидно, что одним из базисных решений является следующее:
В общем случае число базисных решений не превышает 3. Если
где хотя бы один из элементов Таким образом, метод Жордана-Гаусса состоит из r итераций (r шагов). На каждой S -ой итерации выбирается направляющий элемент Рассмотрим алгоритм произвольной итерации метода Жордана-Гаусса. Положим Шаг 1. Сформировать множество Шаг 2. Если Шаг 3. Если для Шаг 4. Разделить направляющую строку Шаг 5. К i -ой строке, Покажем, что столбец
Полагая j=k, из (4.4.1) и (4.4.3) имеем
Пример. Решить систему линейных уравнений методом Жордана-Гаусса.
Решение. Составим из данной системы расширенную матрицу
Полагаем Итерация 1. Шаг 1. Шаг 2. Шаг 3. Находим Шаг 4. Делим третью строку на Шаг 5. К первой, второй и четвертой строкам прибавляем третью строку, соответственно умноженную на -2, -2, -3. В результате матрица
Итерация 2. Шаг 1. Шаг 2. Шаг 3. Находим Шаг 4. Делим первую строку на Шаг 5. Ко второй, третьей и четвертой строкам прибавляем первую строку, соответственно умноженную на -4, -3, 1. Получим матрицу
Итерация 3. Шаг 1. Шаг 2. Шаг 3. Находим Шаг 4. Делим четвертую строку на Шаг 5. К первой, второй, третьей строкам прибавляем четвертую строку, соответственно умноженную на 0, -5, -2. Получим матрицу
Итерация 4. Шаг 1.
Шаг 2. Шаг 3. Находим Шаг 4. Делим четвертую строку на Шаг 5. К первой, третьей и четвертой строкам прибавляем вторую строку, соответственно умноженную на -1, 2, 0. Получим матрицу
Итерация 5. Шаг 1. Шаг 2.
Решение. Составим расширенную матрицу
В результате итерации 1, полагая
После итерации 2, полагая
Итерация 3. Шаг 1. Шаг 2. Шаг 3. Так как Матрица
Получим одно из базисных решений:
Решение. Матрицы
Очевидно, что процесс элементарных преобразований следует закончить, так как Используя метод Жордана-Гаусса, рассмотрим еще один метод вычисления обратной матрицы Рассмотрим матричное уравнение
где Очевидно, что матричное уравнение (4.4.5) имеет единственное решение Решение матричного уравнения (4.4.5) сводится к решению n систем n линейных уравнений с n неизвестными вида
Системе линейных уравнений (4.4.6) соответствует расширенная матрица Таким образом, чтобы для невырожденной матрицы А вычислить обратную матрицу Пример. Вычислить обратную матрицу
Решение. Составим матрицу
На итерации 1, полагая
На итерации 2, полагая
На итерации 3, полагая
откуда
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 661; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.118.218 (0.014 с.) |


 – неизвестные, подлежащие определению;
– неизвестные, подлежащие определению; – числа, называемые коэффициентами при неизвестных;
– числа, называемые коэффициентами при неизвестных; – числа, называемые свободными членами.
– числа, называемые свободными членами. таких, что если в каждое уравнение системы вместо неизвестных подставить эти числа (
таких, что если в каждое уравнение системы вместо неизвестных подставить эти числа ( вместо
вместо  ,
,  вместо
вместо  вместо
вместо  ), то все уравнения обратятся в тождества.
), то все уравнения обратятся в тождества. и расширенную матрицу
и расширенную матрицу ,
,

 , обе части второго равенства умножим на алгебраическое дополнение
, обе части второго равенства умножим на алгебраическое дополнение  и т.д. и обе части n -ого равенства – на
и т.д. и обе части n -ого равенства – на  . Складывая левые и правые части полученных выражений, придем к следующему равенству:
. Складывая левые и правые части полученных выражений, придем к следующему равенству:
 равен определителю | A | системы (4.2.1), коэффициент при
равен определителю | A | системы (4.2.1), коэффициент при  равен нулю, а правая часть равенства (4.2.3) является определителем, полученным из определителя | A | путем замены j -го столбца столбцом свободных членов.
равен нулю, а правая часть равенства (4.2.3) является определителем, полученным из определителя | A | путем замены j -го столбца столбцом свободных членов.

 , откуда
, откуда
 .
. ,
,  при
при  ,
,  .
. .
.
 :
:
 ,
, ,
, ,
,
 .
.


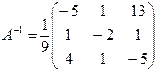 .
. ,
,
 .
. .
.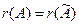 .
. является линейной комбинацией всех остальных столбцов, взятых соответственно с коэффициентами
является линейной комбинацией всех остальных столбцов, взятых соответственно с коэффициентами  . Отсюда следует, что максимальное число линейно независимых столбцов матриц А и
. Отсюда следует, что максимальное число линейно независимых столбцов матриц А и 
 являются решением системы (4.1.1), т.е. система (4.1.1) совместна. Теорема доказана.
являются решением системы (4.1.1), т.е. система (4.1.1) совместна. Теорема доказана. , то система (4.1.1) несовместна;
, то система (4.1.1) несовместна; . Тогда систему, состоящую из первых r уравнений системы (4.1.1)
. Тогда систему, состоящую из первых r уравнений системы (4.1.1)
 . Рассмотрим первые r уравнений системы (4.1.1). Оставив в левых частях первые r неизвестных, перенесем остальные в правые части. Получим систему:
. Рассмотрим первые r уравнений системы (4.1.1). Оставив в левых частях первые r неизвестных, перенесем остальные в правые части. Получим систему:
 , то система (4.1.1) несовместна.
, то система (4.1.1) несовместна. . Тогда если
. Тогда если  . Тогда первым уравнением системы будет уравнение
. Тогда первым уравнением системы будет уравнение .
. . Затем умножим это же уравнение на
. Затем умножим это же уравнение на  , и прибавим его почленно к уравнениям системы с номерами i=2,3,…,m. После этого преобразования в уравнениях с номерами i >1 будет исключено неизвестное х 1. Первый шаг метода Жордана-Гаусса закончен.
, и прибавим его почленно к уравнениям системы с номерами i=2,3,…,m. После этого преобразования в уравнениях с номерами i >1 будет исключено неизвестное х 1. Первый шаг метода Жордана-Гаусса закончен. .
. , но найдется хотя бы одно уравнение, в котором сохранится неизвестное
, но найдется хотя бы одно уравнение, в котором сохранится неизвестное  . Одно из таких уравнений примем в качестве второго уравнения системы. В этом случае расширенная матрица
. Одно из таких уравнений примем в качестве второго уравнения системы. В этом случае расширенная матрица  , соответствующая полученной системе, имеет вид:
, соответствующая полученной системе, имеет вид: .
. .
. , содержащую r единичных столбцов на месте первых n столбцов матрицы А (r – ранг матрицы А системы).
, содержащую r единичных столбцов на месте первых n столбцов матрицы А (r – ранг матрицы А системы). , то матрица
, то матрица 
 .
.

 называются базисными.
называются базисными.  – свободными неизвестными.
– свободными неизвестными. .
. .
.
 отличен от нуля. В этом случае система (4.1.1) несовместна.
отличен от нуля. В этом случае система (4.1.1) несовместна. соответственно направляющие строка и столбец. С помощью элементарных преобразований столбец
соответственно направляющие строка и столбец. С помощью элементарных преобразований столбец  преобразуется в единичный с единицей в строке
преобразуется в единичный с единицей в строке  .
. .
. .
. , то процесс элементарных преобразований закончить. В противном случае перейти к шагу 3.
, то процесс элементарных преобразований закончить. В противном случае перейти к шагу 3. , то процесс элементарных преобразований закончить. В противном случае найти направляющий элемент
, то процесс элементарных преобразований закончить. В противном случае найти направляющий элемент  и перейти к шагу 4.
и перейти к шагу 4. .
. , прибавим строку
, прибавим строку  .
. . Элементы матрицы
. Элементы матрицы  выражаются через элементы матрицы
выражаются через элементы матрицы  следующим образом:
следующим образом:



 .
.

 .
. .
. , переходим к шагу 3.
, переходим к шагу 3. .
. .
. преобразуется в матрицу
преобразуется в матрицу .
. .
. .
. .
. .
.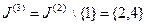 .
. .
. .
. .
. .
.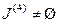 , переходим к шагу 3.
, переходим к шагу 3. .
. .
. .
. , поэтому процесс элементарных преобразований закончен. На основании вида матрицы
, поэтому процесс элементарных преобразований закончен. На основании вида матрицы  получаем единственное решение исходной системы:
получаем единственное решение исходной системы:  .
.
 .
. , получим матрицу
, получим матрицу
 , получим матрицу
, получим матрицу
 .
. .
. , то процесс элементарных преобразований закончен.
, то процесс элементарных преобразований закончен. определяет общее решение системы:
определяет общее решение системы:
 – базисные,
– базисные,  – свободные переменные.
– свободные переменные. .
.



 . Из первой (или третьей) строки матрицы
. Из первой (или третьей) строки матрицы  , которое не может быть удовлетворено ни при каких значениях неизвестных
, которое не может быть удовлетворено ни при каких значениях неизвестных  .
. .
. ,
,
 , Е – единичная матрица.
, Е – единичная матрица. .
.
 . Применяя к матрице
. Применяя к матрице  алгоритм метода Жордана-Гаусса, получим матрицу
алгоритм метода Жордана-Гаусса, получим матрицу  . Покажем, что
. Покажем, что  . Расширенной матрице
. Расширенной матрице  соответствует матричное уравнение
соответствует матричное уравнение  , которое имеет единственное решение Х=В. Матрица
, которое имеет единственное решение Х=В. Матрица  методом Жордана-Гаусса. Поэтому системы линейных уравнений, соответствующие матрицам
методом Жордана-Гаусса. Поэтому системы линейных уравнений, соответствующие матрицам  и
и  , равносильны, т.е. имеют одно и то же решение. Отсюда следует, что
, равносильны, т.е. имеют одно и то же решение. Отсюда следует, что  .
. . Методом Жордана-Гаусса в матрице
. Методом Жордана-Гаусса в матрице  .
. .
. .
. , получим
, получим .
. , получим
, получим ,
, .
.


