
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изоморфизм векторных пространствСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Векторные пространства R и R’ называются изоморфными, если между их векторами-элементами можно установить взаимно однозначное соответствие такое, что если Из определения изоморфизма следует, что если Пространства различной размерности не могут быть между собой изоморфны. В самом деле, пусть R и R' изоморфны. Тогда максимальное число линейно независимых векторов в R и R' одно и то же, т.е. размерности пространств R и R' равны. Все пространства, имеющие одну и ту же размерность n, изоморфны между собой.
5.5. Преобразование координат при изменении базиса
Пусть
Выражения (5.5.1) показывают, что новые базисные векторы
причем коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрица. Матрица А называется матрицей перехода от базиса Определитель матрицы А отличен от нуля, так как в противном случае ее столбцы, а следовательно, и векторы Рассмотрим, как связаны между собой координаты одного и того же вектора
и в то же время
Подставим в (5.5.3) вместо
Из (5.5.2) и (5.5.4) в силу единственности разложения вектора
или в матричном виде
где Уравнение (5.5.5.) показывает связь между координатами хj и x'j вектора Из (5.5.5.) получаем: X'=А-1Х Таким образом, при переходе от базиса Пример. В базисе Решение. Векторы
методом Жордана-Гаусса.
откуда Система векторов Выразим каждый вектор
Матрица А перехода от базиса
Вычислив
определим координаты
Таким образом, в базисе Связь между базисом
или в матричном виде: E=XA, где
Решение данного матричного уравнения имеет вид X=A-1, откуда получаем
Данные соотношения выражают связь между базисами.
Евклидово пространство n -мерное векторное пространство Еn называется евклидовым, если каждой паре векторов I. Линейности по первому аргументу
II. Симметрии
III. Положительной определенности
и Из линейности по первому аргументу и симметрии следует и линейность по второму аргументу
Примеры. 1. Векторами пространства En является любая упорядоченная система n действительных чисел Легко убедиться в том, что аксиомы I-III действительно выполняются. 2. Рассмотрим более общий случай. Вектор Зададимся некоторой квадратной матрицей А=(aij)n,n, Скалярное произведение векторов
Рассмотрим, каким условиям должна удовлетворять матрица А, чтобы определенное данной формулой скалярное произведение удовлетворяло бы аксиомам I-Ш. Непосредственной проверкой можно убедиться в том, что аксиома I выполняется для любой матрицы А=(aij)n,n. Для того, чтобы была выполнена аксиома II, т.е. чтобы выражение Аксиома III требует, чтобы выражение
было неотрицательно для любых Однородный многочлен (квадратичная форма), определяемый формулой (5.6.2), называется положительно определенным, если он принимает неотрицательные значения и обращается в нуль, только тогда, когда все Если а качестве матрицы А=(aij)n,n взять единичную матрицу Е, т.е. положить aii =1, а aij =0 (
и мы получаем евклидово пространство, определенное в примере 1. 3. Векторами пространства Еn будем называть непрерывные функции, заданные на интервале (а,b). Скалярное произведение таких функций определим как интеграл их произведения
Можно проверить, что при таком определении скалярного произведения аксиомы I-III выполнены. С помощью введенного понятия скалярного произведения определим длину вектора и угол между векторами. Определение. Нормой (длиной)
Векторы В любом евклидовом пространстве Еn верна «теорема Пифагора»: если
Определение. Угол между ненулевыми векторами
Можно доказать, что в любом пространстве Еn справедливо неравенство Коши-Буняковского:
откуда следует, что
или, что то же самое,
Это означает, что косинус угла между векторами из Еn по модулю, не превосходит единицы. Если
Число Определение. Система векторов Система векторов
Теорема. Ортогональная система ненулевых векторов пространства Еn линейно независима. Доказательство. Пусть ненулевые векторы Покажем, что векторное равенство
выполняется тогда и только тогда, когда
из условия ортогональности векторов имеем
Следовательно, Рассмотрим процесс ортогонализации векторов. Он состоит в том, что из заданных линейно независимых векторов Допустим теперь, что попарно ортогональные и отличные от нуля векторы
т.е. вектор
Так как векторы
……………………………
откуда
Докажем теперь, что построенный вектор
откуда следует, что Теорема. Во всяком евклидовом пространстве Еn существуют ортонормированные базисы. Доказательство. По определению n -мерного векторного пространства в нем существует некоторый базис
Найдем выражение скалярного произведения в координатах. Пусть
Тогда
Если Пусть Определим в пространстве Еn расстояние между векторами. Расстояние
Из определения расстояния следует, что 1) 2) 3) 4) Пример. По заданной в Еn системе линейно независимых векторов Решение. Полагаем
Тогда Находим вектор
Находим нормы векторов
Нормируем векторы
5.7. Ортогональные преобразования
Рассмотрим свойства матрицы перехода от одного ортонормированного базиса к другому ортонормированному базису в пространстве Еn. Введем понятие ортогональной матрицы. Определение. Матрица Т с вещественными элементами называется ортогональной, если Из определения следует, что ортогональная матрица всегда невырожденная, так как Основные свойства ортогональной матрицы. 1. Матрица, обратная ортогональной, также ортогональна. Пусть Т – ортогональная матрица, т.е. 2. Матрица
Линейное преобразование Y=ТХ с ортогональной матрицей Т называется ортогональным. Так как Теорема. Ортогональное преобразование координат не изменяет скалярного произведения векторов. Доказательство. Рассмотрим линейный оператор Поэтому Следствие 1. Ортогональное преобразование не меняет норм векторов и углов между векторами. Следствие 2. Ортогональное преобразование переводит ортонормированный базис в ортонормированный. Следствие 3. Матрица Т перехода от одного ортонормированного базиса к другому ортонормированному базису является ортогональной. Следствие 4. Матрица Т, приводящая симметричную матрицу А к диагональному виду, является ортогональной.
Выпуклые множества
Рассмотрим совместную систему линейных уравнений
у которой ранг r матрицы Определение. Множество точек Очевидно, что каждую гиперплоскость можно задать всего одним линейным уравнением:
В трехмерном пространстве Е3 гиперплоскости – это обычные плоскости, а в Е2 – это прямые. Определение. Отрезком
Точки Определение. Множество Х пространства Еn называется выпуклым, если вместе с любыми двумя точками Выпуклость множества Х означает, что из Определение. Множество Х точек пространства Еn называется ограниченным, если координаты всех его точек Пусть в пространстве задана гиперплоскость Теорема. Каждое полупространство пространства Еn является выпуклым множеством. Доказательство. Пусть точки
Если
Для этой точки
т.е. произвольная точка Теорема. Пересечение любого числа выпуклых множеств есть множество выпуклое. Доказательство. Пусть Из данной теоремы следует, что гиперплоскость как пересечение выпуклых множеств Х1 и Х2, является выпуклым множеством. Каждая k -мерная плоскость в Еn также выпукла. Пусть в Еn даны m полупространств, определяемых неравенствами
Пересечение этих полупространств, называемое выпуклой многогранной областью, определяет множество решений системы линейных неравенств (5.8.2). Если это пересечение ограничено, оно называется выпуклым многогранником в Еn. Определение. Последовательность
Множество Определение. Множество Определение. Точка Определение. Точка Определение. Точка Для круга любая точка ограничивающей его окружности является крайней. Крайними точками являются все вершины выпуклого многогранника. Определение. Точка Например, любая внутренняя точка круга является выпуклой комбинацией концов хорды, проходящей через эту точку. Теорема (о представлении). Любая точка Пример. Используя теорему о представлении, выразить точку
Решение. Очевидно, что множество Х выпукло. Множество Х (рис.5.1) представляет собой треугольник с вершинами
В координатной форме получим два уравнения:
Добавляя к данной системе условие
откуда Все эти коэффициенты удовлетворяют условию неотрицательности: | |||||||||||||||||||||||||||||||||
|
| Поделиться: |

 и
и  , где
, где  ,
,  , то
, то  и
и  .
. ,... – векторы из R, a
,... – векторы из R, a  ,... – вектора из R', то равенство
,... – вектора из R', то равенство  равносильно равенству
равносильно равенству  . Следовательно, линейно независимым векторам из R соответствуют линейно независимые векторы из R' и обратно.
. Следовательно, линейно независимым векторам из R соответствуют линейно независимые векторы из R' и обратно. и
и  – два базиса пространства Rn. Каждый вектор
– два базиса пространства Rn. Каждый вектор 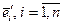 можно выразить через векторы
можно выразить через векторы  :
: ,
,
 ……………………………
……………………………

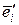 получаются из старых базисных векторов
получаются из старых базисных векторов  с помощью матрицы:
с помощью матрицы: ,
, к базису
к базису  .
. были бы линейно зависимы.
были бы линейно зависимы.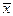 в старом и новом базисах. Пусть
в старом и новом базисах. Пусть

 их выражения из (5.5.1):
их выражения из (5.5.1):
 ,
, ,
,  .
. и
и  .
. ,
,  ,
,  пространства R3 заданы векторы
пространства R3 заданы векторы  ,
,  ,
,  ,
,  . Показать, что векторы
. Показать, что векторы  образует базис. Найти координаты вектора
образует базис. Найти координаты вектора  в базисе
в базисе  выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда  ,
,  ,
,  . Найдем решение векторного равенства
. Найдем решение векторного равенства 
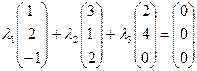




 .
. через векторы
через векторы 


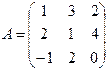 .
.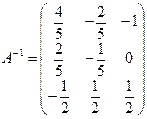 ,
, вектора
вектора  .
.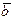 определяется координатами
определяется координатами  .
.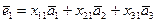 ,
, ,
, ,
, .
. ,
, ,
, ,
, из Е поставлено в соответствие вещественное число (
из Е поставлено в соответствие вещественное число ( ;
; ;
; , при
, при 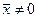
 тогда и только тогда, когда
тогда и только тогда, когда  .
.
 . Сложение векторов и умножение их на число определены в п.5.1, а скалярное произведение векторов
. Сложение векторов и умножение их на число определены в п.5.1, а скалярное произведение векторов  и
и 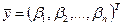 определим формулой
определим формулой  .
. по-прежнему определим как упорядоченную совокупность n действительных чисел. Сложение векторов и умножение их на число определим так же, как в примере 1.
по-прежнему определим как упорядоченную совокупность n действительных чисел. Сложение векторов и умножение их на число определим так же, как в примере 1.
 было симметричным относительно
было симметричным относительно  , т.е. чтобы матрица А=(aij)n,n, была симметричной.
, т.е. чтобы матрица А=(aij)n,n, была симметричной.
 и обращалось в нуль лишь если
и обращалось в нуль лишь если  .
. равны нулю. Следовательно, аксиома III требует, чтобы квадратичная форма (5.6.2) была положительно определенной. Таким образом, всякая матрица А=(aij)n,n задает скалярное произведение в Еn, определяемое формулой (5.6.1), если только эта матрица симметричная и соответствующая ей квадратичная форма положительно определенная.
равны нулю. Следовательно, аксиома III требует, чтобы квадратичная форма (5.6.2) была положительно определенной. Таким образом, всякая матрица А=(aij)n,n задает скалярное произведение в Еn, определяемое формулой (5.6.1), если только эта матрица симметричная и соответствующая ей квадратичная форма положительно определенная. ), то скалярное произведение принимает вид
), то скалярное произведение принимает вид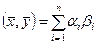
 .
. вектора
вектора  .
. .
.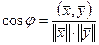 .
. ,
,

 между ними равен
между ними равен 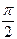 . Ненулевой вектор
. Ненулевой вектор  и достаточно взять
и достаточно взять 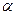 таким, чтобы
таким, чтобы
 пространства Еn называется ортогональной, если векторы этой системы попарно ортогональны.
пространства Еn называется ортогональной, если векторы этой системы попарно ортогональны. .
. .
.
 . Умножим обе части равенства (5.6.3) скалярно на
. Умножим обе части равенства (5.6.3) скалярно на  . Получим
. Получим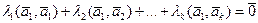
 ,
,  ,
,  .
. . Аналогично, умножая (5.6.3) на
. Аналогично, умножая (5.6.3) на  , получим что
, получим что  и т.д. Таким образом, мы доказали, что
и т.д. Таким образом, мы доказали, что 
 строятся m попарно ортогональных векторов
строятся m попарно ортогональных векторов 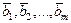 . Положим
. Положим  . Вектор
. Вектор  будем искать в виде
будем искать в виде  . Число
. Число  следует подобрать так, чтобы векторы
следует подобрать так, чтобы векторы  и
и  , откуда
, откуда  .
.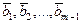 уже построены. Вектор
уже построены. Вектор  ищем в виде:
ищем в виде: ,
, «исправлением» его с помощью линейной комбинации уже построенных векторов
«исправлением» его с помощью линейной комбинации уже построенных векторов  находим из условия ортогональности вектора
находим из условия ортогональности вектора 
 попарно ортогональны, то из равенств (5.6.4) получаем
попарно ортогональны, то из равенств (5.6.4) получаем ,
,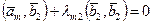 ,
, ,
, .
. . Но вектор
. Но вектор  можно заменить линейной комбинацией вектора
можно заменить линейной комбинацией вектора  и векторов
и векторов  и т.д. Окончательно мы получаем, что вектор
и т.д. Окончательно мы получаем, что вектор 
 . Действительно, в противном случае левая часть равенства (5.6.5) была бы равна
. Действительно, в противном случае левая часть равенства (5.6.5) была бы равна  , что противоречит линейной независимости векторов
, что противоречит линейной независимости векторов  . По векторам
. По векторам  , можно построить вектор
, можно построить вектор  . Продолжая этот процесс, можно по заданной системе n линейно независимых векторов в Еn построить систему n ненулевых ортогональных векторов. Докажем следующую теорему.
. Продолжая этот процесс, можно по заданной системе n линейно независимых векторов в Еn построить систему n ненулевых ортогональных векторов. Докажем следующую теорему. . С помощью процесса ортогонализации из него можно построить ортогональный базис
. С помощью процесса ортогонализации из него можно построить ортогональный базис  . Если теперь каждый вектор
. Если теперь каждый вектор  разделить на его норму, то получится ортонормированный базис, образованный векторами
разделить на его норму, то получится ортонормированный базис, образованный векторами .
. произвольный базис пространства Еn и
произвольный базис пространства Еn и .
. .
. ,
, 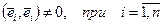 а, значит
а, значит  . И обратно, если в базисе
. И обратно, если в базисе  , то этот базис ортонормированный, так как в этом случае
, то этот базис ортонормированный, так как в этом случае  , то этот базис ортонормированный.
, то этот базис ортонормированный. получим
получим  , т.е. i -я координата вектора
, т.е. i -я координата вектора  между векторами
между векторами  :
: .
. ;
; ;
; ;
; для любых
для любых  из
из 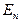 .
.

 построить ортонормированный базис.
построить ортонормированный базис.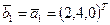 . Вектор
. Вектор  .
. .
.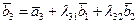 .
.
 .
. .
.

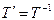 т.е.
т.е.  .
. и
и  , то
, то  .
. , т.е.
, т.е. 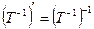 . Значит, матрица
. Значит, матрица  – ортогональна.
– ортогональна. ортогональна тогда и только тогда, когда ее элементы удовлетворяют равенствам
ортогональна тогда и только тогда, когда ее элементы удовлетворяют равенствам .
. , соответствующий матрице Т, и два произвольных вектора
, соответствующий матрице Т, и два произвольных вектора 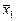 и
и  , т.е.
, т.е.  ,
,  . Тогда
. Тогда  .
.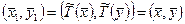 .
.
 меньше n, и пусть k=n-r.
меньше n, и пусть k=n-r. из Еn, координаты которых удовлетворяют системе уравнений (5.8.1), называется k -мерной плоскостью. Одномерные плоскости называются прямыми, а (n-1)-мерные плоскости – гиперплоскостями.
из Еn, координаты которых удовлетворяют системе уравнений (5.8.1), называется k -мерной плоскостью. Одномерные плоскости называются прямыми, а (n-1)-мерные плоскости – гиперплоскостями. .
. в Еn, соединяющим точки
в Еn, соединяющим точки 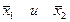 , называется множество таких точек
, называется множество таких точек 
 ему принадлежит и соединяющих их отрезок
ему принадлежит и соединяющих их отрезок  следует
следует  для всех
для всех  . Например, в Е2 выпуклый отрезок, полупрямая, круг, треугольник, полуплоскость и вся плоскость.
. Например, в Е2 выпуклый отрезок, полупрямая, круг, треугольник, полуплоскость и вся плоскость. в некотором базисе ограничены.
в некотором базисе ограничены. и
и  – множество точек, для которых
– множество точек, для которых 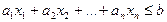 .
. и
и  из Еn принадлежат, например, полупространству Х1. Тогда
из Еn принадлежат, например, полупространству Х1. Тогда
 , то
, то

 – выпуклые множества в Еn. Если
– выпуклые множества в Еn. Если  состоит из одной точки, то оно выпукло. Если более чем из одной, то пусть
состоит из одной точки, то оно выпукло. Если более чем из одной, то пусть  и, так как все множества
и, так как все множества  выпуклы, то
выпуклы, то  и, следовательно,
и, следовательно, 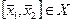 , что и требовалось доказать.
, что и требовалось доказать. .
.
 точек в Еn сходится к точке
точек в Еn сходится к точке  , если
, если .
.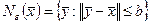 называется
называется  окрестностью точки
окрестностью точки  называется замкнутым, если оно содержит все свои предельные точки.
называется замкнутым, если оно содержит все свои предельные точки. из Еn называется внутренней точкой множества Х, если существует такая ее
из Еn называется внутренней точкой множества Х, если существует такая ее  -окрестность, все точки которой принадлежат множеству Х.
-окрестность, все точки которой принадлежат множеству Х. из Еn называется граничной точкой множества Х, если любая ее
из Еn называется граничной точкой множества Х, если любая ее 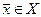 называется крайней точкой (вершиной), если в Х не существует точек
называется крайней точкой (вершиной), если в Х не существует точек  , что
, что  .
. , если существуют такие числа
, если существуют такие числа  , что
, что 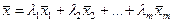 при условии
при условии  .
.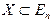 может быть представлена в виде выпуклой комбинации конечного числа крайних точек этого множества.
может быть представлена в виде выпуклой комбинации конечного числа крайних точек этого множества. в виде выпуклой комбинации крайних точек множества
в виде выпуклой комбинации крайних точек множества  , заданного системой неравенств
, заданного системой неравенств

 . На основании теоремы о представлении точку
. На основании теоремы о представлении точку  .
.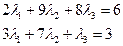
 , получим систему трех линейных уравнений с тремя неизвестными. Решая систему методом Жордана-Гаусса, получаем
, получим систему трех линейных уравнений с тремя неизвестными. Решая систему методом Жордана-Гаусса, получаем ,
,
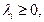
 . Поэтому искомое представление имеет вид
. Поэтому искомое представление имеет вид 


