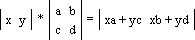Растровая и векторная графика

 

Таким образом, выбор растрового или векторного формата зависит от целей и задач работы с изображением. Если нужна фотографическая точность цветопередачи, то предпочтительнее растр. Логотипы, схемы, элементы оформления удобнее представлять в векторном формате. Понятно, что и в растровом и в векторном представлении графика (как и текст) выводятся на экран монитора или печатное устройство в виде совокупности точек. В Интернете графика представляется в одном из растровых форматов, понимаемых броузерами без установки дополнительных модулей – GIF, JPG, PNG. Без дополнительных плагинов (дополнений) наиболее распространенные броузеры понимают только растровые форматы –.gif,.jpg и.png (последний пока мало распространен). На первый взгляд, использование векторных редакторов становится неактуальным. Однако большинство таких редакторов обеспечивают экспорт в.gif или.jpg с выбираемым Вами разрешением. А рисовать начинающим художникам проще именно в векторных средах – если рука дрогнула и линия пошла не туда, получившийся элемент легко редактируется. При рисование в растровом режиме Вы рискуете непоправимо испортить фон.

Из-за описанных выше особенностей представления изображения, для каждого типа приходится использовать отдельный графический редактор – растровый или векторный. Разумеется, у них есть общие черты – возможность открывать и сохранять файлы в различных форматах, использование инструментов с одинаковыми названиями (карандаш, перо и т.д.) или функциями (выделение, перемещение, масштабирование и т.д.), выбирать нужный цвет или оттенок...

Однако принципы реализации процессов рисования и редактирования различны и обусловлены природой соответствующего формата. Так, если в растровых редакторах говорят о выделении объекта, то имеют в виду совокупность точек в виде области сложной формы. Процесс выделения очень часто является трудоемкой и кропотливой работой. При перемещении такого выделения появляется«дырка». В векторном же редакторе объект представляет совокупность графических примитивов и для его выделения достаточно выбрать мышкой каждый из них. А если эти примитивы были сгруппированы соответствующей командой, то достаточно «щелкнуть» один раз в любой из точек сгруппированного объекта. Перемещение выделенного объекта обнажает нижележащие элементы.

Тем не менее, существует тенденция к сближению. Большинство современных векторных редакторов способны использовать растровые картинки в качестве фона, а то и переводить в векторный формат части изображения встроенными средствами (трассировка). Причем обычно имеются средства редактирования загруженного фонового изображения хотя бы на уровне различных встроенных или устанавливаемых фильтров. 8-я версия Illustrator'a способна загружать.psd-файлы Photoshop'a и использовать каждый из полученных слоев. Кроме того, для использования тех же фильтров, может осуществляться непосредственный перевод сформированного векторного изображения в растровый формат и дальнейшее использование как нередактируемого растрового элемента. Причем, все это помимо обычно имеющихся конвертеров из векторного формата в растровый с получением соответствующего файла.

 

3 Преобразования в двухмерном пространстве

 

Преобразования в двухмерном пространстве используются в разнообразных случаях: чтобы отдельные части объекта можно было описывать в различных координатных системах; чтобы типовые и повторяющиеся части можно было располагать в произвольных положениях на чертеже и в пространстве, в том числе с использованием циклов; чтобы без повторной кодировки можно было получать симметричные части объекта; для направленной деформации фигур, тел и их частей; для изменения масштаба чертежа, построения проекций пространственных образов... С аналитической точки зрения преобразования - это пересчет значений координат.

 

Преобразование точки

 

Точка на плоскости представляется двумя координатами: |x y|. Матрица преобразования точки выглядит так:

Ниже показано преобразование точки через квадратную матрицу; здесь x_n = xa + yc и y_n = xb + yd - новые координаты точки после преобразования:

Преобразование фигуры

 

Если представить фигуру как совокупность точек, то можно провести и ее преобразование. В следующем примере задано четыре точки: A(0, 0), B(1, 0), C(1, 1), D(0, 1), каждая из которых после преобразования переходит соответственно в A^*(0, 0), B^*(a, b), C^*(a + c, b + d), D^*(c, d):

Геометрически это соответствует деформации фигуры:

При этом площадь новой фигуры равна площади старой фигуры, умноженной на детерминант матрицы преобразования: S₂ = S₁ * |ad - bc|.