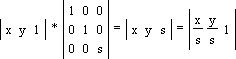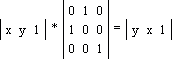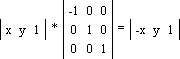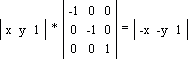Математические основы векторной графики

Растровая графика

 

Для растровых изображений, состоящих из точек, особую важность имеет понятие разрешения, выражающее количество точек, приходящихся на единицу длины. При этом следует различать:

разрешение оригинала;

разрешение экранного изображения;

разрешение печатного изображения.

Разрешение оригинала. Разрешение оригинала измеряется в точках на дюйм (dots per inch – dpi) и зависит от требований к качеству изображения и размеру файла, способу оцифровки и создания исходной иллюстрации, избранному формату файла и другим параметрам. В общем случае действует правило: чем выше требование к качеству, тем выше должно быть разрешение оригинала.

Разрешение экранного изображения. Для экранных копий изображения элементарную точку растра принято называть пикселом. Размер пиксела варьируется в зависимости от выбранного экранного разрешения (из диапазона стандартных значений), разрешение оригинала и масштаб отображения.

Мониторы для обработки изображений с диагональю 20–21 дюйм (профессионального класса), как правило, обеспечивают стандартные экранные разрешения 640х480, 800х600, 1024х768, 1280х1024, 1600х1200, 1600х1280, 1920х1200, 1920х1600 точек. Расстояние между соседними точками люминофора у качественного монитора составляет 0,22–0,25 мм.

Для экранной копии достаточно разрешения 72 dpi, для распечатки на цветном или лазерном принтере 150–200 dpi, для вывода на фотоэкспонирующем устройстве 200–300 dpi. Установлено эмпирическое правило, что при распечатке величина разрешения оригинала должна быть в 1,5 раза больше, чем линиатура растра устройства вывода. В случае, если твердая копия будет увеличена по сравнению с оригиналом, эти величины следует умножить на коэффициент масштабирования.

Разрешение печатного изображения и понятие линиатуры. Размер точки растрового изображения как на твердой копии (бумага, пленка и т. д.), так и на экране зависит от примененного метода и параметров растрирования

оригинала. При растрировании на оригинал как бы накладывается сетка линий, ячейки которой образуют элемент растра. Частота сетки растра измеряется числом линий на дюйм (lines per inch – lpi) и называется линиатурой.

Размер точки растра рассчитывается для каждого элемента и зависит от интенсивности тона в данной ячейке. Чем больше интенсивность, тем плотнее заполняется элемент растра. То есть, если в ячейку попал абсолютно черный цвет, размер точки растра совпадет с размером элемента растра. В этом случае говорят о 100% заполняемости. Для абсолютно белого цвета значение заполняемости составит 0%. На практике заполняемость элемента на отпечатке обычно составляет от 3 до 98%. При этом все точки растра имеют одинаковую оптическую плотность, в идеале приближающуюся к абсолютно черному цвету.

Иллюзия более темного тона создается за счет увеличения размеров точек и, как следствие, сокращения пробельного поля между ними при одинаковом расстоянии между центрами элементов растра. Такой метод называют растрированием с амплитудной модуляцией (AM).

Интенсивность тона (так называемую светлоту) принято подразделять на 256 уровней. Большее число градаций не воспринимается зрением человека и является избыточным. Меньшее число ухудшает восприятие изображения (минимально допустимым для качественной полутоновой иллюстрации принято значение 150 уровней). Нетрудно подсчитать, что для воспроизведения 256 уровней тона достаточно иметь размер ячейки растра 256 = 16 х 16 точек.

При выводе копии изображения на принтере или полиграфическом оборудовании линиатуру растра выбирают, исходя из компромисса между требуемым качеством, возможностями аппаратуры и параметрами печатных материалов. Для лазерных принтеров рекомендуемая линиатура составляет 65-100 Ipi, для газетного производства – 65-85 lpi, для книжно-журнального – 85-133 lpi, для художественных и рекламных работ – 133-300 lpi.

При печати изображений с наложением растров друг на друга, например многоцветных, каждый последующий растр поворачивается на определенный угол. Традиционными для цветной печати считаются углы поворота: 105 градусов для голубой печатной формы, 75 градусов для пурпурной, 90 градусов для желтой и 45 градусов для черной. При этом ячейка растра становится косоугольной, и для воспроизведения 256 градаций тона с линиатурой 150 lpi уже недостаточно разрешения 16х150=2400 dpi.

Поэтому для фотоэкспонирующих устройств профессионального класса принято минимальное стандартное разрешение 2540 dpi, обеспечивающее качественное растрирование при разных углах поворота растра. Таким образом, коэффициент, учитывающий поправку на угол поворота растра, для цветных изображений составляет 1,06.

Динамический диапазон. Качество воспроизведения тоновых изображений принято оценивать динамическим диапазоном (D). Это оптическая плотность, численно равная десятичному логарифму величины, обратной коэффициенту пропускания [pic](для оригиналов, рассматриваемых “на просвет”, например слайдов) или коэффициенту отражения [pic](для прочих оригиналов, например полиграфических отпечатков).

Для оптических сред, пропускающих свет, динамический диапазон лежит в пределах от 0 до 4. Для поверхностей, отражающих свет, значение динамического диапазона составляет от 0 до 2. Чем выше динамический диапазон, тем большее число полутонов присутствует в изображении и тем лучше качество его восприятия.

Связь между параметрами изображения и размером файла. Средствами растровой графики принято иллюстрировать работы, требующие высокой точности в передаче цветов и полутонов. Однако размеры файлов растровых иллюстраций стремительно растут с увеличением разрешения. Фотоснимок, предназначенный для домашнего просмотра (стандартный размер 10х15 см, оцифрованный с разрешением 200-300 dpi, цветовое разрешение 24 бита), занимает в формате TIFF с включенным режимом сжатия около 4 Мбайт. Оцифрованный с высоким разрешением слайд занимает 45-50 Мбайт. Цветоделенное цветное изображение формата А4 занимает 120-150 Мбайт.

Масштабирование растровых изображений. Одним из недостатков растровой графики является так называемая пикселизация изображений при их увеличении (если не приняты специальные меры). Раз в оригинале присутствует определенное количество точек, то при большем масштабе увеличивается и их размер, становятся заметны элементы растра, что искажает саму иллюстрацию. Для противодействия пикселизации принято заранее оцифровывать оригинал с разрешением, достаточным для качественной визуализации при масштабировании. Другой прием состоит в применении стохастического растра, позволяющего уменьшить эффект пикселизации в определенных пределах. Наконец, при масштабировании используют метод интерполяции, когда увеличение размера иллюстрации происходит не за счет масштабирования точек, а путем добавления необходимого числа промежуточных точек.

 

Векторная графика

 

Если в растровой графике базовым элементом изображения является точка, то в векторной графике – линия. Линия описывается математически как единый объект, и потому объем данных для отображения объекта средствами векторной графики существенно меньше, чем в растровой графике.

Линия – элементарный объект векторной графики. Как и любой объект, линия обладает свойствами: формой (прямая, кривая), толщиной, цветом, начертанием (сплошная, пунктирная). Замкнутые линии приобретают свойство заполнения. Охватываемое ими пространство может быть заполнено другими объектами (текстуры, карты) или выбранным цветом. Простейшая незамкнутая линия ограничена двумя точками, именуемыми узлами. Узлы также имеют свойства, параметры которых влияют на форму конца линии и характер сопряжения с другими объектами. Все прочие объекты векторной графики составляются из линий. Например, куб можно составить из шести связанных прямоугольников, каждый из которых, в свою очередь, образован четырьмя связанными линиями. Возможно, представить куб и как двенадцать связанных линий, образующих ребра.

 

Операция смещения

 

Матрица преобразования содержит в себе константы m и n, под действием которых точка смещается на m единиц вдоль оси x и на n единиц - вдоль оси y:

Операция масштабирования

За счет коэффициентов a и d матрицы преобразования происходит увеличение (или уменьшение) значения координат точки (x, y) в a и d раз по осям x и y соответственно:

Общее полное масштабирование

В данном случае при s < 1 будет происходить увеличение значения координат точки (x, y) в s раз; при s > 1 мы получим обратный эффект - уменьшение значения координат (x, y) в s раз.

Поворот на угол θ

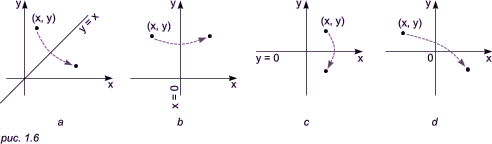
Здесь θ - угол, на который требуется повернуть точку (x, y). Обратите внимание: поворот происходит относительно точки (0, 0) декартовой системы координат против часовой стрелки!

Отображение или зеркалирование

Зеркалирование относительно прямой y = x (рис. 1.6a):

· Зеркалирование относительно прямой x = 0 (рис. 1.6b):

· Зеркалирование относительно прямой y = 0 (рис. 1.6c):

· Зеркалирование относительно начала координат (рис. 1.6d):

·

 

Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол α

 

Чтобы провести любое сложное преобразование, необходимо разложить его на базовые операции. Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол α состоит из трех базовых операций: 1) перенос фигуры на вектор A(-m, -n) для совмещения точки (m, n) с началом координат; 2) поворот фигуры на угол α; 3) перенос фигуры на вектор A'(m, n) для возвращения ее в исходное положение. Так как фигуру можно представить набором точек, то операции 1) - 3) можно выполнять последовательно для каждой точки. Покажем это на примере.

Пусть мы хотим повернуть треугольник с координатами A(x, y), B(x1, y1), C(x2, y2) вокруг точки D(m, n) на угол α. Пусть P-s - матрица переноса точки на вектор A(-m, -n), V_α- матрица поворота на угол α, Ps - матрица переноса точки на вектор A'(m, n).

Итак, мы имеем все данные, необходимые для проведения сложного преобразования первой точки - A(x, y):

Точно такие же преобразования необходимо провести для оставшихся двух точек треугольника, подставляя соответствующие их координаты взамен x и y (последовательность операций см. на рис. 1.7). Таким образом, сложная операция разбивается на простейшие и задается произведением соответствующих матриц преобразования, причем порядок, в котором перемножаются матрицы, существенно определяет результат.

Центральное проецирование (перспектива)

px + qy + 1 = H - плоскость.

Примечания

1. В общем случае от перемены матриц местами результат меняется.

2. Матрицы операций, идущие подряд, можно перемножать раздельно, главное - не менять их порядок следования (см. примечание 1).

3. Линии при описанных выше (аффинных) преобразованиях переходят в линии. Поэтому обычно производится пересчет только координат вершин фигуры, а после этого соответствующие вершины в результирующей фигуре соединяются, как и в исходной фигуре.

 

Нахождение точки пересечения двух линий

 

Пусть имеются две линии: x + y = 1, 2x - 3y = 0, необходимо найти точку их пересечения. Решение может быть найдено с использованием матриц. Перенесем все члены уравнений в левую часть: x + y - 1 = 0, 2x - 3y - 0 = 0; запишем коэффициенты первого уравнения в первый столбец матрицы, второго уравнения - во второй:

Условие, при котором пересекаются две прямые, выглядит следующим образом:

|x y 1| * M = |0 0 1|

Для нахождения ответа необходимо обе части предыдущего уравнения домножить справа на обратную матрицу M-1 (при перемножении M и M-1 получается единичная матрица E):

|x y 1| * E = |0 0 1| * M-1

|x y 1| = |3/5 2/5 1|

Ответ: точка пересечения прямых: x = 3/5, y = 2/5.

 

Аффинное проецирование

· Геометрия аффинная

· Аксонометрическая (прямоугольная) проекция

· Ортографическая проекция

· Ортогональная проекция

· Диметрическая проекция

· Изометрическая проекция

· Косоугольная проекция

· Проекция Кабине

· Проекция Кавалье

· Геометрия перспективная

· Перспективная проекция

· Одноточечная проекция

· Двухточечная проекция

· Трехточечная проекция

Аффинная геометрия является чертежным средством; в этой геометрии используется параллельное проецирование, которое осуществляется пучком параллельных прямых (см. рис. 3.1, слева). Детерминант матрицы преобразований в аффинной геометрии равен нулю. Геометрия перспективная является художественным средством, в ней отсутствуют параллельные линии и используется центральное проецирование, при котором все линии сходятся у горизонта в одну точку (см. рис. 3.1, справа); за счет того, что одна, две или три компоненты четвертого столбца матрицы преобразований не равны нулю, ее детерминант также не равен нулю.

Наиболее распространены аффинные двухмерные и трехмерные преобразования. Их основные геометрические свойства: прямые линии после преобразования остаются прямыми, параллельные - параллельными, плоскости остаются плоскостями и параллельные плоскости - параллельными. Вычерчивание трехмерных объектов, независимо от того на бумаге ли это происходит или на экране дисплея, осуществляется при помощи двухмерных проекций. В плоской проекции каждая точка предмета проецируется определенным образом на плоскость проекции, и ее образ называется точкой проекции. Если линии проекции, соединяющие точки предмета с соответствующими точками проекции, параллельны, то мы имеем плоскую параллельную проекцию. Если же линии проекции сходятся в одной общей точке, то получаемое изображение называется центральной проекцией, или перспективным изображением предмета.

Рассмотрим далее несколько видов аксонометрических проекций. Заметим, что среди них выделяются прямоугольные (ортогональные) проекции - те, у которых проецирующие лучи перпендикулярны к плоскости изображения. Слова "аксонометрическая" и "прямоугольная" часто используют как синонимы.

 

Перспективное проецирование

 

На фотографиях, картинах, экране изображения кажутся нам естественными и правильными. Эти изображения называют перспективными. Свойства их таковы, что более удаленные предметы изображаются в меньших масштабах, параллельные прямые в общем случае непараллельны. В итоге геометрия изображения оказывается достаточно сложной, и по готовому изображению сложно определить размер тех или иных частей объекта.

Обычная перспективная проекция - это центральная проекция на плоскость прямыми лучами, проходящими через точку - центр проецирования. Один из проецирующих лучей перпендикулярен к плоскости проецирования и называется главным. Точка пересечения этого луча и плоскости проекции - главная точка картины.

Существует три системы координат. Обычно программист работает и держит данные о геометрических объектах в мировых координатах. Для повышения реалистичности при подготовке к выводу изображения на экран данные об объектах из мировых координат переводят в видовые координаты. И только в момент вывода изображения непосредственно на экран дисплея переходят к экранным координатам, которые представляют собой номера пикселов экрана.

Первые две системы могут использоваться в многомерных системах координат, но последняя только в двухмерной. Операции являются необратимыми, то есть из двухмерной картинки-проекции невозможно восстановить трехмерное изображение.

 

Матрица общего перспективного преобразования

 

В этой матрице элементы a, d, е отвечают за масштабирование, m, n, L - за смещение, p, q, r - за проецирование, s - за комплексное масштабирование, х - за вращение.

 

Одноточечное проецирование на плоскость z = 0

 

Суть этого проецирования такова: чем глубже находится предмет, тем больше становится значение z-координаты и знаменателя z + 1, и, следовательно, тем мельче выглядит предмет на плоскости проекции. Выполним несложные выкладки и поясним их графически: уравнение x'/F = x/(F + z_пр) равносильно: x' = xF/(F + z_пр) = x/(1 + z_пр/F) = x/(1 + rz_пр), где r = 1/F, F - фокус.

 

 

Для того, чтобы точки, лежащие на линии, параллельной оси z, не терялись друг за другом, используется одноточечное проецирование на линию (см. матрицу преобразования и рис. 4.2); исчезла z-координата, но поскольку дальние предметы стали более мелкими, чем близкие такие же, то при рассмотрении рисунка у зрителя появляется ощущение глубины.

 

 

А теперь для примера отобразим куб, стороны которого равны единице (см. рис. 4.3), на плоскость z = 0; пусть на оси z фокус F = -10 и, следовательно, r = -1/10 = -0.1:

 

 

В плоскости экрана после преобразования мы будем иметь следующее изображение:

 

 

Обратите внимание, что если бы исходный куб стоял центром тяжести (который находится на пересечении диагоналей куба) в точке (0, 0, 0), то он получился бы более "традиционного" вида:

Двухточечное проецирование

 

Если проекция двухточечная (например, по p <> 0 и q <> 0), то имеется две точки схода на соответствующие оси. Так как по z в данном случае реализуется параллельное проецирование, то удвоения контура куба на экране (x, y) нет. Меняя p и q, мы регулируем точку схода:

 

Форматы графических данных

 

В компьютерной графике применяют по меньшей мере три десятка форматов файлов для хранения изображений. Но лишь часть из них стала стандартом “де-факто” и применяется в подавляющем большинстве программ. Как правило, несовместимые форматы имеют файлы растровых, векторных, трехмерных изображений, хотя существуют форматы, позволяющие хранить данные разных классов. Многие приложения ориентированы на собственные “специфические” форматы, перенос их файлов в другие программы вынуждает использовать специальные фильтры или экспортировать изображения в “стандартный” формат.

TIFF (Tagged Image File Format). Формат предназначен для хранения растровых изображений высокого качества (расширение имени файла.TIF). Относится к числу широко распространенных, отличается переносимостью между платформами (IBM PC и Apple Macintosh), обеспечен поддержкой со стороны большинства графических, верстальных и дизайнерских программ. Предусматривает широкий диапазон цветового охвата – от монохромного черно-белого до 32-разрядной модели цветоделения CMYK. Начиная с версии 6.0 в формате TIFF можно хранить сведения о масках (контурах обтравки) изображений. Для уменьшения размера файла применяется встроенный алгоритм сжатия LZW.

PSD (PhotoShop Document). Собственный формат программы Adobe Photoshop (расширение имени файла.PSD), один из наиболее мощных по возможностям хранения растровой графической информации. Позволяет запоминать параметры слоев, каналов, степени прозрачности, множества масок. Поддерживаются 48-разрядное кодирование цвета, цветоделение и различные цветовые модели. Основной недостаток выражен в том, что отсутствие эффективного алгоритма сжатия информации приводит к большому объему файлов.

PCX. Формат появился как формат хранения растровых данных программы PC PaintBrush фирмы Z-Soft и является одним из наиболее распространенных (расширение имени файла.PCX). Отсутствие возможности хранить цветоделенные изображения, недостаточность цветовых моделей и другие ограничения привели к утрате популярности формата. В настоящее время считается устаревшим.

JPEG (Joint Photographic Experts Group). Формат предназначен для хранения растровых изображений (расширение имени файла.JPG). Позволяет регулировать соотношение между степенью сжатия файла и качеством изображения.

Применяемые методы сжатия основаны на удалении “избыточной” информации, поэтому формат рекомендуют использовать только для электронных публикаций.

GIF (Graphics Interchange Format). Стандартизирован в 1987 году как средство хранения сжатых изображений с фиксированным (256) количеством цветов (расширение имени файла.GIF). Получил популярность в Интернете благодаря высокой степени сжатия. Последняя версия формата GIF89a позволяет выполнять чересстрочную загрузку изображений и создавать рисунки с прозрачным фоном. Ограниченные возможности по количеству цветов обусловливают его применение исключительно в электронных публикациях.

PNG (Portable Network Graphics). Сравнительно новый (1995 год) формат хранения изображений для их публикации в Интернете (расширение имени файла.PNG). Поддерживаются три типа изображений – цветные с глубиной 8 или 24 бита и черно-белое с градацией 256 оттенков серого. Сжатие информации происходит практически без потерь, предусмотрены 254 уровня альфа-канала, чересстрочная развертка.

WMF (Windows MetaFile). Формат хранения векторных изображений операционной системы Windows (расширение имени файла.WMF). По определению поддерживается всеми приложениями этой системы. Однако отсутствие средств для работы со стандартизированными цветовыми палитрами, принятыми в полиграфии, и другие недостатки ограничивают его применение.

EPS (Encapsulated PostScript). Формат описания как векторных, так и растровых изображений на языке PostScript фирмы Adobe, фактическом стандарте в области допечатных процессов и полиграфии (расширение имени файла.EPS). Так как язык PostScript является универсальным, в файле могут одновременно храниться векторная и растровая графика, шрифты, контуры обтравки (маски), параметры калибровки оборудования, цветовые профили. Для отображения на экране векторного содержимого используется формат WMF, а растрового – TIFF. Но экранная копия лишь в общих чертах отображает реальное изображение, что является существенным недостатком EPS.

Действительное изображение можно увидеть лишь на выходе выводного устройства, с помощью специальных программ просмотра или после преобразования файла в формат PDF в приложениях Acrobat Reader, Acrobat Exchange.

PDF (Portable Document Format). Формат описания документов, разработанный фирмой Adobe (расширение имени файла.PDF). Хотя этот формат в основном предназначен для хранения документа целиком, его впечатляющие возможности позволяют обеспечить эффективное представление изображений. Формат является аппаратно-независимьм, поэтому вывод изображений допустим на любых устройствах – от экрана монитора до фотоэкспонирующего устройства. Мощный алгоритм сжатия со средствами управления итоговым разрешением изображения обеспечивает компактность файлов при высоком качестве иллюстраций.

 

 

Adobe Photoshop

 

В обширном классе программ для обработки растровой графики особое место занимает пакет Photoshop компании Adobe. По сути дела, сегодня он является стандартом в компьютерной графике, и все другие программы неизменно сравнивают именно с ним.

Главные элементы управления программы Adobe Photoshop сосредоточены в строке меню и панели инструментов. Особую группу составляют диалоговые окна – инструментальные палитры:

Палитра Кисти управляет настройкой параметров инструментов редактирования. В режим редактирования кисти входят после двойного щелчка на ее изображении в палитре. Щелчок при нажатой клавише CTRL уничтожает кисть. Двойным щелчком на свободном поле палитры открывают диалоговое окно формирования новой кисти, которая автоматически добавляется в палитру.

Палитра Параметры служит для редактирования свойств текущего инструмента. Открыть ее можно не только из строки меню, но и двойным щелчком на значке инструмента в панели инструментов. Состав элементов управления палитры зависит от выбранного инструмента.

Палитра Инфо обеспечивает информационную поддержку средств отображения. На ней представлены: текущие координаты указателя мыши, размер текущей выделенной области, цветовые параметры элемента изображения и другие данные.

Палитра Навигатор позволяет просмотреть различные фрагменты изображения и изменить масштаб просмотра. В окне палитры помещена миниатюра изображения с выделенной областью просмотра.

Палитра Синтез отображает цветовые значения текущих цветов переднего плана и фона. Ползунки на цветовой линейке соответствующей цветовой системы позволяют редактировать эти параметры.

Палитра Каталог содержит набор доступных цветов. Такой набор можно загрузить и отредактировать, добавляя и удаляя цвета. Цветовой тон переднего плана и фона выбирают из состава набора. В стандартном комплекте поставки программы предусмотрено несколько цветовых наборов, в основном компании Pantone.

Палитра Слои служит для управления отображением всех слоев изображения, начиная с самого верхнего. Возможно определение параметров слоев, изменение их порядка, операции со слоями с применением разных методов.

Палитру Каналы используют для выделения, создания, дублирования и удаления каналов, определения их параметров, изменения порядка, преобразования каналов в самостоятельные объекты и формирования совмещенных изображений из нескольких каналов.

Палитра Контуры содержит список всех созданных контуров. При преобразовании контура в выделенную область его используют для формирования обтравочного контура.

Палитра Операции позволяет создавать макрокоманды – заданную последовательность операций с изображением. Макрокоманды можно записывать, выполнять, редактировать, удалять, сохранять в виде файлов.

Особую группу программных средств обработки изображений представляют Фильтры. Это подключаемые к программе модули, часто третьих фирм, позволяющие обрабатывать изображение по заданному алгоритму. Иногда такие алгоритмы бывают очень сложными, а окно фильтра может иметь множество настраиваемых параметров. Из групп фильтров популярны продукты серий Kai's Power Tools, Alien Skin, Andromeda и другие.

 

Растровая графика

 

Для растровых изображений, состоящих из точек, особую важность имеет понятие разрешения, выражающее количество точек, приходящихся на единицу длины. При этом следует различать:

разрешение оригинала;

разрешение экранного изображения;

разрешение печатного изображения.

Разрешение оригинала. Разрешение оригинала измеряется в точках на дюйм (dots per inch – dpi) и зависит от требований к качеству изображения и размеру файла, способу оцифровки и создания исходной иллюстрации, избранному формату файла и другим параметрам. В общем случае действует правило: чем выше требование к качеству, тем выше должно быть разрешение оригинала.

Разрешение экранного изображения. Для экранных копий изображения элементарную точку растра принято называть пикселом. Размер пиксела варьируется в зависимости от выбранного экранного разрешения (из диапазона стандартных значений), разрешение оригинала и масштаб отображения.

Мониторы для обработки изображений с диагональю 20–21 дюйм (профессионального класса), как правило, обеспечивают стандартные экранные разрешения 640х480, 800х600, 1024х768, 1280х1024, 1600х1200, 1600х1280, 1920х1200, 1920х1600 точек. Расстояние между соседними точками люминофора у качественного монитора составляет 0,22–0,25 мм.

Для экранной копии достаточно разрешения 72 dpi, для распечатки на цветном или лазерном принтере 150–200 dpi, для вывода на фотоэкспонирующем устройстве 200–300 dpi. Установлено эмпирическое правило, что при распечатке величина разрешения оригинала должна быть в 1,5 раза больше, чем линиатура растра устройства вывода. В случае, если твердая копия будет увеличена по сравнению с оригиналом, эти величины следует умножить на коэффициент масштабирования.

Разрешение печатного изображения и понятие линиатуры. Размер точки растрового изображения как на твердой копии (бумага, пленка и т. д.), так и на экране зависит от примененного метода и параметров растрирования

оригинала. При растрировании на оригинал как бы накладывается сетка линий, ячейки которой образуют элемент растра. Частота сетки растра измеряется числом линий на дюйм (lines per inch – lpi) и называется линиатурой.

Размер точки растра рассчитывается для каждого элемента и зависит от интенсивности тона в данной ячейке. Чем больше интенсивность, тем плотнее заполняется элемент растра. То есть, если в ячейку попал абсолютно черный цвет, размер точки растра совпадет с размером элемента растра. В этом случае говорят о 100% заполняемости. Для абсолютно белого цвета значение заполняемости составит 0%. На практике заполняемость элемента на отпечатке обычно составляет от 3 до 98%. При этом все точки растра имеют одинаковую оптическую плотность, в идеале приближающуюся к абсолютно черному цвету.

Иллюзия более темного тона создается за счет увеличения размеров точек и, как следствие, сокращения пробельного поля между ними при одинаковом расстоянии между центрами элементов растра. Такой метод называют растрированием с амплитудной модуляцией (AM).

Интенсивность тона (так называемую светлоту) принято подразделять на 256 уровней. Большее число градаций не воспринимается зрением человека и является избыточным. Меньшее число ухудшает восприятие изображения (минимально допустимым для качественной полутоновой иллюстрации принято значение 150 уровней). Нетрудно подсчитать, что для воспроизведения 256 уровней тона достаточно иметь размер ячейки растра 256 = 16 х 16 точек.

При выводе копии изображения на принтере или полиграфическом оборудовании линиатуру растра выбирают, исходя из компромисса между требуемым качеством, возможностями аппаратуры и параметрами печатных материалов. Для лазерных принтеров рекомендуемая линиатура составляет 65-100 Ipi, для газетного производства – 65-85 lpi, для книжно-журнального – 85-133 lpi, для художественных и рекламных работ – 133-300 lpi.

При печати изображений с наложением растров друг на друга, например многоцветных, каждый последующий растр поворачивается на определенный угол. Традиционными для цветной печати считаются углы поворота: 105 градусов для голубой печатной формы, 75 градусов для пурпурной, 90 градусов для желтой и 45 градусов для черной. При этом ячейка растра становится косоугольной, и для воспроизведения 256 градаций тона с линиатурой 150 lpi уже недостаточно разрешения 16х150=2400 dpi.

Поэтому для фотоэкспонирующих устройств профессионального класса принято минимальное стандартное разрешение 2540 dpi, обеспечивающее качественное растрирование при разных углах поворота растра. Таким образом, коэффициент, учитывающий поправку на угол поворота растра, для цветных изображений составляет 1,06.

Динамический диапазон. Качество воспроизведения тоновых изображений принято оценивать динамическим диапазоном (D). Это оптическая плотность, численно равная десятичному логарифму величины, обратной коэффициенту пропускания [pic](для оригиналов, рассматриваемых “на просвет”, например слайдов) или коэффициенту отражения [pic](для прочих оригиналов, например полиграфических отпечатков).

Для оптических сред, пропускающих свет, динамический диапазон лежит в пределах от 0 до 4. Для поверхностей, отражающих свет, значение динамического диапазона составляет от 0 до 2. Чем выше динамический диапазон, тем большее число полутонов присутствует в изображении и тем лучше качество его восприятия.

Связь между параметрами изображения и размером файла. Средствами растровой графики принято иллюстрировать работы, требующие высокой точности в передаче цветов и полутонов. Однако размеры файлов растровых иллюстраций стремительно растут с увеличением разрешения. Фотоснимок, предназначенный для домашнего просмотра (стандартный размер 10х15 см, оцифрованный с разрешением 200-300 dpi, цветовое разрешение 24 бита), занимает в формате TIFF с включенным режимом сжатия около 4 Мбайт. Оцифрованный с высоким разрешением слайд занимает 45-50 Мбайт. Цветоделенное цветное изображение формата А4 занимает 120-150 Мбайт.

Масштабирование растровых изображений. Одним из недостатков растровой графики является так называемая пикселизация изображений при их увеличении (если не приняты специальные меры). Раз в оригинале присутствует определенное количество точек, то при большем масштабе увеличивается и их размер, становятся заметны элементы растра, что искажает саму иллюстрацию. Для противодействия пикселизации принято заранее оцифровывать оригинал с разрешением, достаточным для качественной визуализации при масштабировании. Другой прием состоит в применении стохастического растра, позволяющего уменьшить эффект пикселизации в определенных пределах. Наконец, при масштабировании используют метод интерполяции, когда увеличение размера иллюстрации происходит не за счет масштабирования точек, а путем добавления необходимого числа промежуточных точек.

 

Векторная графика

 

Если в растровой графике базовым элементом изображения является точка, то в векторной графике – линия. Линия описывается математически как единый объект, и потому объем данных для отображения объекта средствами векторной графики существенно меньше, чем в растровой графике.

Линия – элементарный объект векторной графики. Как и любой объект, линия обладает свойствами: формой (прямая, кривая), толщиной, цветом, начертанием (сплошная, пунктирная). Замкнутые линии приобретают свойство заполнения. Охватываемое ими пространство может быть заполнено другими объектами (текстуры, карты) или выбранным цветом. Простейшая незамкнутая линия ограничена двумя точками, именуемыми узлами. Узлы также имеют свойства, параметры которых влияют на форму конца линии и характер сопряжения с другими объектами. Все прочие объекты векторной графики составляются из линий. Например, куб можно составить из шести связанных прямоугольников, каждый из которых, в свою очередь, образован четырьмя связанными линиями. Возможно, представить куб и как двенадцать связанных линий, образующих ребра.

 

Математические основы векторной графики

 

Рассмотрим подробнее способы представления различных объектов в векторной графике.

Точка. Этот объект на плоскости представляется двумя числами (х, у), указывающими его положение относительно начала координат.

Прямая линия. Ей соответствует уравнение y=kx+b. Указав параметры k и b, всегда можно отобразить бесконечную прямую линию в известной системе координат, то есть для задания прямой достаточно двух параметров.

Отрезок прямой. Он отличается тем, что требует для описания еще двух параметров – например, координат x1 и х2 начала и конца отрезка.

Кривая второго порядка. К этому классу кривых относятся параболы, гиперболы, эллипсы, окружности, то есть все линии, уравнения которых содержат степени не выше второй. Кривая второго порядка не имеет точек перегиба. Прямые линии являются всего лишь частным случаем кри