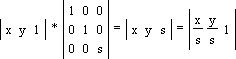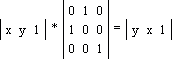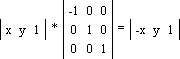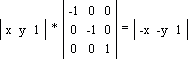Однородные координаты. Операции в них

 

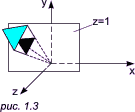
Любая система координат, в которой представление точки в двухмерном (трехмерном) пространстве задается при помощи трех (четырех) координат (Р₁, Р₂, Р₃(, Р₄)), называется системой однородных координат. Вообще, для n-мерного пространства число однородных координат должно быть на единицу больше: n + 1.

Применение однородных координат в общем случае позволяет устранять аномалии, возникающие при работе в декартовых координатах, и представлять сложные преобразования в виде произведения нескольких матриц.

Геометрическая интерпретация на случай двухмерного пространства: введение третьей координаты, равной единице, можно трактовать как переход в трехмерное пространство, в котором разрешено работать только в плоскости z = 1. Следует представлять себе, что экран компьютера (картинная плоскость, плоскость изображения) находится в плоскости z = 1:

В случае выхода рисунка за сечение z = 1 рисунок возвращается принудительно в данное сечение - для того, чтобы были возможны последующие операции:

Такая операция называется нормализацией однородных координат:

Общий вид преобразования

 

Операция смещения

 

Матрица преобразования содержит в себе константы m и n, под действием которых точка смещается на m единиц вдоль оси x и на n единиц - вдоль оси y:

Операция масштабирования

За счет коэффициентов a и d матрицы преобразования происходит увеличение (или уменьшение) значения координат точки (x, y) в a и d раз по осям x и y соответственно:

Общее полное масштабирование

В данном случае при s < 1 будет происходить увеличение значения координат точки (x, y) в s раз; при s > 1 мы получим обратный эффект - уменьшение значения координат (x, y) в s раз.

Поворот на угол θ

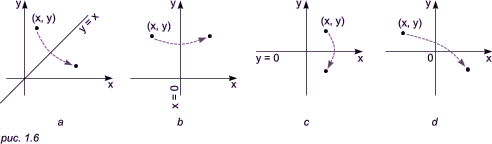
Здесь θ - угол, на который требуется повернуть точку (x, y). Обратите внимание: поворот происходит относительно точки (0, 0) декартовой системы координат против часовой стрелки!

Отображение или зеркалирование

Зеркалирование относительно прямой y = x (рис. 1.6a):

· Зеркалирование относительно прямой x = 0 (рис. 1.6b):

· Зеркалирование относительно прямой y = 0 (рис. 1.6c):

· Зеркалирование относительно начала координат (рис. 1.6d):

·

 

Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол α

 

Чтобы провести любое сложное преобразование, необходимо разложить его на базовые операции. Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол α состоит из трех базовых операций: 1) перенос фигуры на вектор A(-m, -n) для совмещения точки (m, n) с началом координат; 2) поворот фигуры на угол α; 3) перенос фигуры на вектор A'(m, n) для возвращения ее в исходное положение. Так как фигуру можно представить набором точек, то операции 1) - 3) можно выполнять последовательно для каждой точки. Покажем это на примере.

Пусть мы хотим повернуть треугольник с координатами A(x, y), B(x1, y1), C(x2, y2) вокруг точки D(m, n) на угол α. Пусть P-s - матрица переноса точки на вектор A(-m, -n), V_α- матрица поворота на угол α, Ps - матрица переноса точки на вектор A'(m, n).

Итак, мы имеем все данные, необходимые для проведения сложного преобразования первой точки - A(x, y):

Точно такие же преобразования необходимо провести для оставшихся двух точек треугольника, подставляя соответствующие их координаты взамен x и y (последовательность операций см. на рис. 1.7). Таким образом, сложная операция разбивается на простейшие и задается произведением соответствующих матриц преобразования, причем порядок, в котором перемножаются матрицы, существенно определяет результат.

Центральное проецирование (перспектива)

px + qy + 1 = H - плоскость.

Примечания

1. В общем случае от перемены матриц местами результат меняется.

2. Матрицы операций, идущие подряд, можно перемножать раздельно, главное - не менять их порядок следования (см. примечание 1).

3. Линии при описанных выше (аффинных) преобразованиях переходят в линии. Поэтому обычно производится пересчет только координат вершин фигуры, а после этого соответствующие вершины в результирующей фигуре соединяются, как и в исходной фигуре.

 

Нахождение точки пересечения двух линий

 

Пусть имеются две линии: x + y = 1, 2x - 3y = 0, необходимо найти точку их пересечения. Решение может быть найдено с использованием матриц. Перенесем все члены уравнений в левую часть: x + y - 1 = 0, 2x - 3y - 0 = 0; запишем коэффициенты первого уравнения в первый столбец матрицы, второго уравнения - во второй:

Условие, при котором пересекаются две прямые, выглядит следующим образом:

|x y 1| * M = |0 0 1|

Для нахождения ответа необходимо обе части предыдущего уравнения домножить справа на обратную матрицу M-1 (при перемножении M и M-1 получается единичная матрица E):

|x y 1| * E = |0 0 1| * M-1

|x y 1| = |3/5 2/5 1|

Ответ: точка пересечения прямых: x = 3/5, y = 2/5.

 

Аффинное проецирование

· Геометрия аффинная

· Аксонометрическая (прямоугольная) проекция

· Ортографическая проекция

· Ортогональная проекция

· Диметрическая проекция

· Изометрическая проекция

· Косоугольная проекция

· Проекция Кабине

· Проекция Кавалье

· Геометрия перспективная

· Перспективная проекция

· Одноточечная проекция

· Двухточечная проекция

· Трехточечная проекция

Аффинная геометрия является чертежным средством; в этой геометрии используется параллельное проецирование, которое осуществляется пучком параллельных прямых (см. рис. 3.1, слева). Детерминант матрицы преобразований в аффинной геометрии равен нулю. Геометрия перспективная является художественным средством, в ней отсутствуют параллельные линии и используется центральное проецирование, при котором все линии сходятся у горизонта в одну точку (см. рис. 3.1, справа); за счет того, что одна, две или три компоненты четвертого столбца матрицы преобразований не равны нулю, ее детерминант также не равен нулю.

Наиболее распространены аффинные двухмерные и трехмерные преобразования. Их основные геометрические свойства: прямые линии после преобразования остаются прямыми, параллельные - параллельными, плоскости остаются плоскостями и параллельные плоскости - параллельными. Вычерчивание трехмерных объектов, независимо от того на бумаге ли это происходит или на экране дисплея, осуществляется при помощи двухмерных проекций. В плоской проекции каждая точка предмета проецируется определенным образом на плоскость проекции, и ее образ называется точкой проекции. Если линии проекции, соединяющие точки предмета с соответствующими точками проекции, параллельны, то мы имеем плоскую параллельную проекцию. Если же линии проекции сходятся в одной общей точке, то получаемое изображение называется центральной проекцией, или перспективным изображением предмета.

Рассмотрим далее несколько видов аксонометрических проекций. Заметим, что среди них выделяются прямоугольные (ортогональные) проекции - те, у которых проецирующие лучи перпендикулярны к плоскости изображения. Слова "аксонометрическая" и "прямоугольная" часто используют как синонимы.