
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторное произведение двух векторов.Содержание книги
Поиск на нашем сайте
Определение. Векторным произведением вектора 1)
3) векторы Векторное произведение означаются 1) 2) 3) 4) Укажем геометрический смысл векторного произведения. Если
Смешанное произведение трех векторов. Определение. Произведение Если известны декартовы координаты векторов
Перечислим свойства смешанного произведения: 1) 2) 3) Можно доказать, что модуль смешанного произведения численно равен объему параллелепипеда, или одной второй объема призмы, или одной шестой объема пирамиды, построенных на
Аналитическая геометрия Прямая в пространстве. Каноническим уравнением прямой, проходящей через точку
Вектор называется направляющим
Плоскость в пространстве. Общим уравнением плоскости в пространстве называется уравнение
Вектор
Если даны три точки
Задание 1. По координатам вершины пирамиды 1. длину ребер 2. угол между ребрами 3. площадь грани 4. объем пирамиды 5. уравнение прямых 6. уравнения плоскостей
7. угол между плоскостями Пример. Выполнить задание 1, если 1) Если заданы точки а)
б)
2) Угол между ребрами
Скалярное произведение
Тогда
Откуда (вычисления проводим на инженерном калькуляторе)
3)
Тогда
4) Учитывая геометрический смысл смешанного произведения векторов, получим формулу для вычисления объема пирамиды:
Найдем координаты вектора
Смешанное произведение этих векторов найдем через их декартовы координаты
Отсюда
5) Найдем канонические уравнение прямых прямая прямая 6) Уравнение плоскости, проходящей через три точки
Составимуравнение плоскости, проходящей через три точки
Разложив определить по первой строке, получим
Итак, уравнение плоскости Аналогично составимуравнение плоскости, проходящей через три точки
Разложив определить по первой строке, получим
Итак, уравнение плоскости 7) Угол
Подставляя их значения из пункта 6) находим величину угла
Задание №2 а) Найти решение системы с помощью правила Крамера; б) Записать систему в матричной форме и решить средствами матричного исчисления. Пример.
а) Составим и вычислим главный и вспомогательные определители системы:
Находим по правилу Крамера решение системы
б) Составим матрицу коэффициентов системы и столбец правых частей
и найдем обратную матрицу по формуле:
где
Составим теперь обратную матрицу
и найдем столбец неизвестных по формуле
Отсюда Задание №3. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления При вычислении предела дробно-рациональной функции при Пример 1. Для вычисления предела этой функции нужно числитель и знаменатель разделить на
(при В том случае, когда при вычислении предела дробно-рациональной функции при Пример 2. Данный предел имеет неопределенность вида
Сократив рациональную дробь на
При вычислении пределов тригонометрических функций часто используется первый замечательный предел
и его следствия:
Пример 3. Преобразовав разность косинусов в произведение, получим
Если в пределе встречается неопределенность Пример 4. Выполнив преобразования и применив второй замечательный предел, найдём
Пример 5. Выполнив преобразования и применив формулу
Задание №4. Исследовать функцию на непрерывность. Найти точки разрыва функции и определить их тип. Функция
Это равенство означает выполнение трех условий: 1) функция 2) функция 3) предел функции в точке Если в точке Точка разрыва х0 называется точкой разрыва первого рода функции При этом: 1) если 2) если Точка разрыва х0 называется точкой разрыва второго рода функции Пример. Дана функция Функция
Следовательно Задание №5. Найти производные первого порядка данных функций, используя правила дифференцирования.
При выполнении данного задания необходимо знать правила дифференцирования (производная суммы, произведения и частного двух функций), а также изучить таблицу производных. Пример. 1)
2)
3) Производная функции, заданной параметрически, вычисляется по формуле:
Тогда Задание №6. Составить уравнения касательной и нормали к графику функции Приведем уравнение касательной, проведенной к графику функции
и уравнение нормали к этой касательной Пример. Для функции 1) Найдем значение функции 2) Найдем значение
3) Составим уравнения касательной и нормали: Задание №7. Найти предел функции с помощью правила Лопиталя. Напомним правило Лопиталя для раскрытия неопределенностей вида Пусть
Замечания: 1) Правило Лопиталя остается справедливым и в том случае, если 2) Если Примеры: 1) 2) 3) Задание №8. Построить график функции Общая схема исследования функции и построения графика. 1. Найти область определения функции. 2. Определить тип функции (четность, нечетность). 3. Найти точки пересечения с осями координат и интервалы знакопостоянства функции. 4. Найти асимптоты графика функции: а) вертикальные; б) невертикальные (наклонные). 5. Найти точки возможного экстремума и интервалы возрастания и убывания функции. 6. Найти точки перегиба и интервалы выпуклости, вогнутости функции. 7. Построить график функции, учитывая проведенные исследования. Пример. Построить график функции 1. Областью определения функции является множество всех действительных чисел, кроме 2. Для определения типа функции найдем значение
Следовательно, функция 3. Так как уравнение
Определим интервалы знакопостоянства функции:
а) Исследуем поведение функции вблизи точки разрыва
Следовательно прямая б). Определим существование наклонной асимптоты:
Следовательно, график функции имеет наклонную асимптоту 5. Для нахождения точек возможного экстремума найдем производную функции:
Приравняем Исследуем знак производной. Для чего решим неравенство
Находим знаки
Следовательно, функция возрастает на промежутках
и убывает на промежутках
По изменению знака
6. Для нахождения точек перегиба и интервалов выпуклости, вогнутости найдем вторую производную функции:
Так как Исследуем знак второй производной, решая неравенство
По результатам исследования строим график функции
Рис.1 Построение графика функции
Задание №9. Найти неопределенные интегралы. Пример. Найти неопределенные интегралы. а) Применим подстановку Таким образом, б) Применим формулу интегрирования по частям
Тогда
К интегралу в правой части снова применяем формулу интегрирования по частям. Пусть
Таким образом,
в) Подынтегральная функция является правильной рациональной дробью, знаменатель которой
Подынтегральную функцию разложим на дроби
откуда
Раскроем скобки в правой части и приведем подобные:
Приравнивая соответствующие коэффициенты при
Таким образом,
Вычислим отдельно интеграл
получаем
Отсюда окончательно вычисляем интеграл
г) Наименьшее общее кратное показателей корней равно 6, поэтому выполним подстановку
Темы практических занятий 1. Элементы линейной и векторной алгебры. Определители их свойства, вычисление. Решение систем линейных уравнений по формулам Крамера. Понятие вектора. Скалярное, векторное и смешанное произведение векторов их свойства, некоторые приложения. 2. Элементы аналитической геометрии. Прямая на плоскости. Различные формы уравнения прямой на плоскости. Прямая в пространстве. Плоскость в пространстве. Взаимное расположение прямой и плоскости. 3. Введение в математический анализ. Предел функции. Односторонние пределы. Предел функции при х→∞. Бесконечно малые и бесконечно большие функции, связь между ними. Основные теоремы о пределах. Первый и второй замечательный пределы. Непрерывность функции. Свойства функций, непрерывных на отрезке. Точки разрыва и их классификация.
4. Дифференциальное исчисление. Производная функции, ее геометрический смысл. Основные правила и формулы дифференцирования. Приложения производной. 5. Функции нескольких переменных. Понятие функции двух и более переменных. Область определения, пределы, непрерывность. Частные производные первого и второго порядков. Экстремумы функции двух переменных. Скалярное поле, градиент, производная по направлению, связь между ними. 5 Содержание и оформление контрольных работ 1. Требования к оформлению контрольных работ: контрольные работы могут выполняться на электронных носителях или в тетради (12 л.) на обложке необходимо указать № к.р., свой факультет, специальность, шифр зачетной книжки, № варианта, ФИО. 2. Требования к структуре контрольной работы: При выполнении работы необходимо приводить основные теоретические моменты, промежуточные математические доказательства, методики, формулы, расчеты. В конце работы указывается список использованных источников, ставится число и личная подпись.
6 Вопросы для подготовки к зачету. 1. Матрицы, основные понятия, действия над матрицами. 2. Определитель, основные свойства. 3. Вычисление определителя третьего порядка. 4. Разложение определителя по строке или столбцу. 5. Системы линейных уравнений, основные понятия. 6. Эквивалентные преобразования системы линейных уравнений. Решение системы линейных уравнений методом Гаусса. 7. Решение системы линейных уравнений методом Крамера. 8. Векторы, основные понятия (длина, проекция вектора на ось, координаты, направляющие косинусы). 9. Линейные операции над векторами, основные свойства. 10. Скалярное произведение векторов, основные свойства. 11. Скалярное произведение в координатной форме. 12. Приложения скалярного произведения. 13. Векторное произведение, основные свойства. 14. Векторное произведение в координатной форме. 15. Приложения векторного произведения. 16. Смешанное произведение, основные свойства. 17. Смешанное произведение в координатной форме. 18. Приложения скалярного произведения. 19. Различные способы задания прямой на плоскости. 20. Взаимное расположение прямых на плоскости. 21. Плоскость и прямая в пространстве. Общее уравнение плоскос
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.107.103 (0.011 с.) |

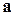 и
и 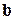 называется вектор
называется вектор 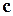 , обладающий следующими свойствами
, обладающий следующими свойствами ,
, 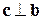 ;
;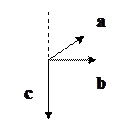 2)
2) 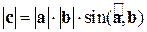 ;
;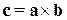 или
или  (антиперестановочный закон);
(антиперестановочный закон);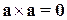 ;
;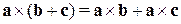 (распределительный закон);
(распределительный закон);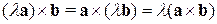 .
. и
и 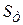 площади соответственно параллелограмма и треугольника, построенных на векторах
площади соответственно параллелограмма и треугольника, построенных на векторах 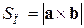 и
и 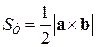 .
. называется смешанным произведением трех векторов
называется смешанным произведением трех векторов 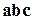 или
или 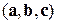 .
.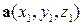 ,
,  ,
, 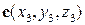 , то
, то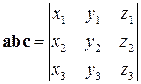 .
.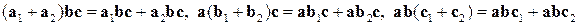 ;
;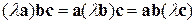 ;
;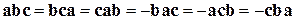 (если поменять местами два любых вектора, то знак смешенного произведения изменится на противоположный, если поменять местами три вектора, то знак не меняется).
(если поменять местами два любых вектора, то знак смешенного произведения изменится на противоположный, если поменять местами три вектора, то знак не меняется). векторах
векторах 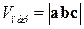 ,
, 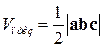 ,
, 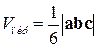 .
.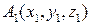 параллельно вектору
параллельно вектору 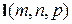 , называется уравнение вида:
, называется уравнение вида: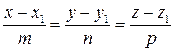 .
.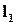 и
и 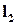 , то косинус угла между этими прямыми определяется по формуле (этот угол всегда острый или прямой)
, то косинус угла между этими прямыми определяется по формуле (этот угол всегда острый или прямой) .
.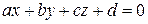 .
. называется нормальным вектором плоскости. Если даны две плоскости с нормальными векторами
называется нормальным вектором плоскости. Если даны две плоскости с нормальными векторами 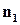 и
и 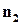 , то косинус угла между этими плоскостями определяется по формуле (этот угол всегда острый или прямой)
, то косинус угла между этими плоскостями определяется по формуле (этот угол всегда острый или прямой)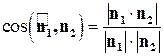 .
.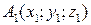 ,
, 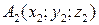 и
и  , то уравнение плоскости, проходящей через три точки находится по формуле:
, то уравнение плоскости, проходящей через три точки находится по формуле: .
.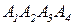 найти:
найти: и
и 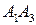 ;
; и
и 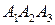 ;
; ;
;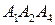 ;
;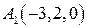 ,
, 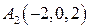 ,
, 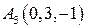 ,
, 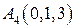 .
.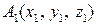 ,
, 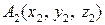 , и
, и 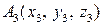 то координаты векторов
то координаты векторов 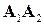 ,
,  и их длины
и их длины 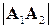 ,
, 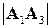 равны:
равны: ,
, .
. ,
,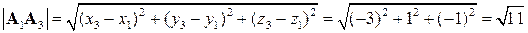 .
.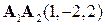 и
и 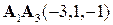 . Из определения скалярного произведения следует, что этот угол вычисляется по формуле:
. Из определения скалярного произведения следует, что этот угол вычисляется по формуле: .
.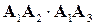 находим через декартовы координаты:
находим через декартовы координаты: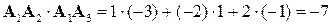 .
.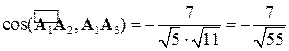 .
.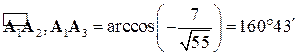
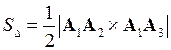 ‑ площадь треугольника, построенного на векторах
‑ площадь треугольника, построенного на векторах 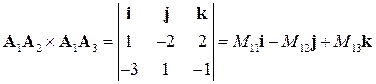 ,
,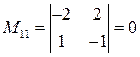 ,
, 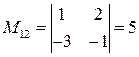 ,
,  .
.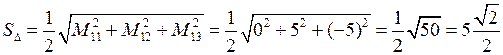 .
. .
.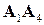 :
:
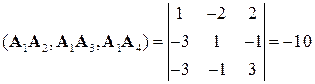 .
.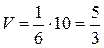 .
.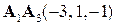 . За точку лежащую на этих векторах примем точку
. За точку лежащую на этих векторах примем точку  ;
;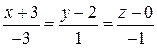 .
. ,
, 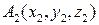 и
и 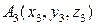 находится по формуле:
находится по формуле: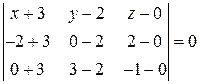 или
или 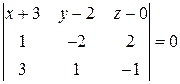 .
.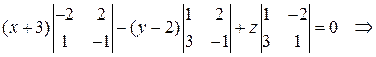
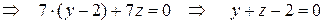 .
.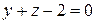 . Коэффициенты уравнения образуют нормальный вектор
. Коэффициенты уравнения образуют нормальный вектор 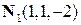 .
.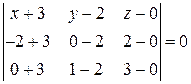 или
или 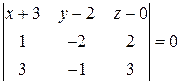 .
.
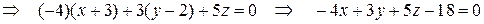 .
. . Коэффициенты уравнения образуют нормальный вектор
. Коэффициенты уравнения образуют нормальный вектор  .
. , образованный двумя плоскостями
, образованный двумя плоскостями 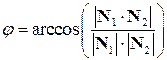 , где
, где 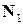 и
и 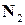 ‑ нормали плоскостей
‑ нормали плоскостей 


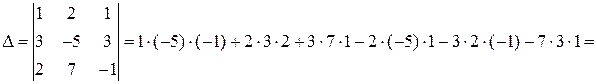
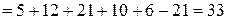 ,
,
 ,
,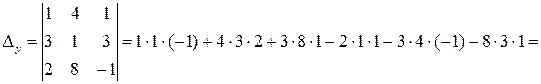
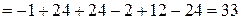 ,
,
 .
.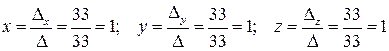 .
.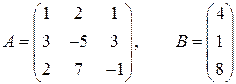 ,
, ,
,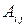 и
и 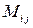 ‑ соответственно алгебраические дополнения и миноры, связанные между собой соотношением
‑ соответственно алгебраические дополнения и миноры, связанные между собой соотношением  , а
, а 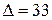 - определитель матрицы
- определитель матрицы 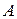 , вычисленный в пункте а). Найдем миноры:
, вычисленный в пункте а). Найдем миноры: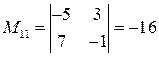 ;
; 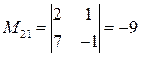 ;
; 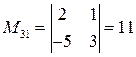 ;
;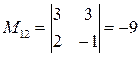 ;
; 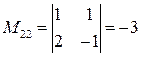 ;
; 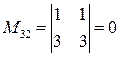 ;
;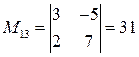 ;
; 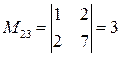 ;
; 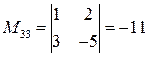 .
.
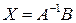 :
: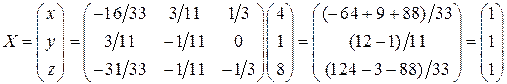 .
.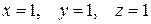 .
.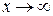 числитель и знаменатель дроби — величины бесконечно большие, т.е. получаем выражение
числитель и знаменатель дроби — величины бесконечно большие, т.е. получаем выражение 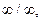 которое представляет собой неопределённость. Для вычисления предела этой функции нужно числитель и знаменатель дроби разделить на наивысшую степень
которое представляет собой неопределённость. Для вычисления предела этой функции нужно числитель и знаменатель дроби разделить на наивысшую степень 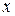 .
. .
.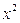 :
: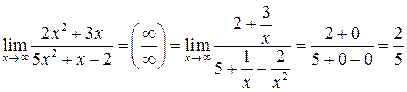 .
.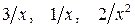 — величины бесконечно малые и, следовательно, их пределы равны нулю).
— величины бесконечно малые и, следовательно, их пределы равны нулю). числитель и знаменатель имеют предел, равный нулю, т.е. имеем неопределенность
числитель и знаменатель имеют предел, равный нулю, т.е. имеем неопределенность  , надо разделить их на
, надо разделить их на 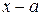 и перейти к пределу. Если после деления окажется, что при
и перейти к пределу. Если после деления окажется, что при 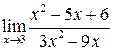 .
.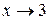 стремятся к 0. Разложим квадратные трёхчлены в числителе и знаменателе рациональной дроби на линейные множители по формуле
стремятся к 0. Разложим квадратные трёхчлены в числителе и знаменателе рациональной дроби на линейные множители по формуле  , где
, где  и
и 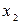 — корни квадратного трёхчлена
— корни квадратного трёхчлена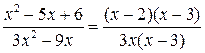 .
. , получим:
, получим: .
.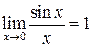
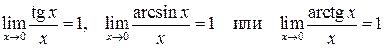 .
. .
. .
. , то используется второй замечательный предел
, то используется второй замечательный предел 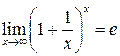 или
или 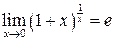 .
.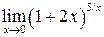 .
. .
.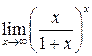 .
.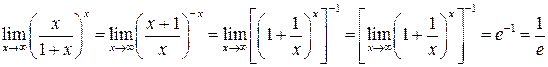 .
. называется непрерывной в точке
называется непрерывной в точке 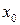 , если предел функции в этой точке равен значению функции в этой точке, т.е.
, если предел функции в этой точке равен значению функции в этой точке, т.е. .
.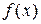 определена в точке х0 и ее окрестности;
определена в точке х0 и ее окрестности;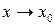 ;
;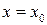 не выполняется по крайней мере одно из условий определения непрерывности функции, то такая точка называется точкой разрыва. Все точки разрыва разделяются на точки разрыва первого и второго рода.
не выполняется по крайней мере одно из условий определения непрерывности функции, то такая точка называется точкой разрыва. Все точки разрыва разделяются на точки разрыва первого и второго рода.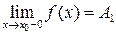 и
и 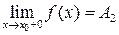 .
. , то точка х0 называется точкой устранимого разрыва;
, то точка х0 называется точкой устранимого разрыва; , то х0 называется точкой конечного разрыва, а величину
, то х0 называется точкой конечного разрыва, а величину 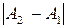 называют скачком функции.
называют скачком функции.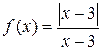 . Найти точки разрыва, определить их тип.
. Найти точки разрыва, определить их тип.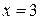 . Очевидно, что
. Очевидно, что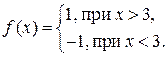 .
. ,
,  . Поэтому в точке
. Поэтому в точке 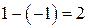 .
.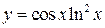 .
.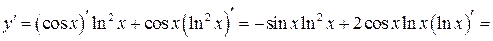
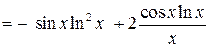 .
.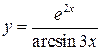 .
.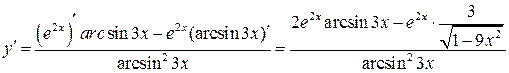 .
. Найти
Найти 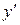 .
.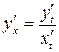 .
.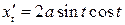 ;
; 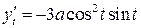 .
.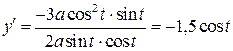 .
.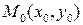 .
. ,
, .
.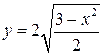 в точке с абсциссой
в точке с абсциссой 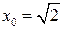 составить уравнение касательной и уравнение нормали.
составить уравнение касательной и уравнение нормали.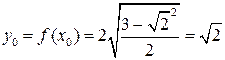 .
.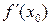 :
: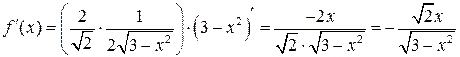 ,
,  .
.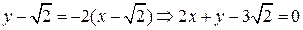 – искомое уравнение касательной;
– искомое уравнение касательной; – искомое уравнение нормали.
– искомое уравнение нормали. и
и  :
: – функции, имеющие производные в некоторой окрестности точки
– функции, имеющие производные в некоторой окрестности точки 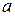 , за исключением, быть может, самой
, за исключением, быть может, самой  точки
точки 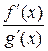 при
при  при
при  .
.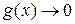
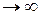 при
при  или при
или при 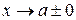 .
. опять дает неопределенность вида
опять дает неопределенность вида 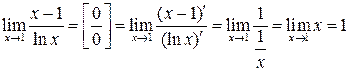 .
. .
. .
. .
.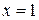 (в этом случае знаменатель равен нулю).
(в этом случае знаменатель равен нулю).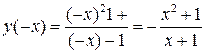 .
. не имеет действительных корней, то график функции не имеет точек пересечения с осью ОХ, но пересекает ось ОУ в точке
не имеет действительных корней, то график функции не имеет точек пересечения с осью ОХ, но пересекает ось ОУ в точке  .
. .
. .
. 4. Найдем асимптоты графика функции.
4. Найдем асимптоты графика функции.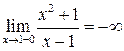 ,
, 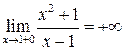 .
.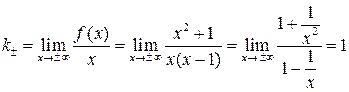 ,
, .
.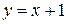 при
при 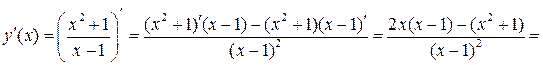
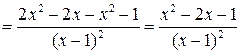 .
.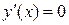 . Решая уравнение
. Решая уравнение 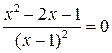 , находим корни производной
, находим корни производной 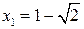 и
и 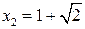 .
.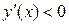
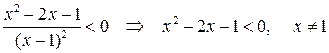
 на промежутках, учитывая корни
на промежутках, учитывая корни 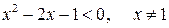 :
: ,
,  ;
; 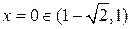 ,
,  ;
;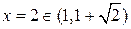 ,
, 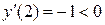 ;
; 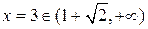 ;
; 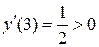 .
.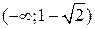 и
и 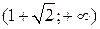 ,
, и
и  .
.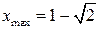 ,
, 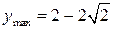 ,
,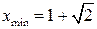 ,
, 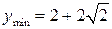 .
.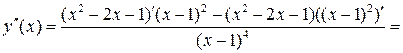
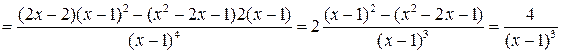 .
.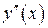 в нуль не обращается, то точек перегиба у функции нет.
в нуль не обращается, то точек перегиба у функции нет.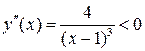 :
: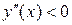 при
при 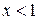 и
и 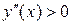 при
при 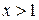 .
. Следовательно, на интервале
Следовательно, на интервале  график направлен выпуклостью вверх (выпуклый), а на интервале
график направлен выпуклостью вверх (выпуклый), а на интервале 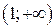 – выпуклостью вниз (вогнутый).
– выпуклостью вниз (вогнутый).
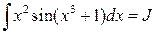 .
. . Тогда
. Тогда 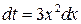 , откуда
, откуда 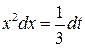 .
.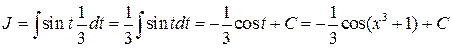
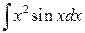 .
.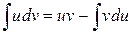 . Пусть
. Пусть ,
,  , тогда
, тогда 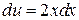 ,
, 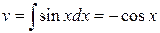 .
.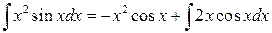 .
.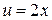 ,
, 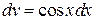 ,
,  ,
, 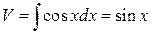
 .
.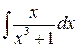
 .
. .
. .
.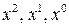 в левой и правой частях последнего равенства получим систему трех уравнений:
в левой и правой частях последнего равенства получим систему трех уравнений: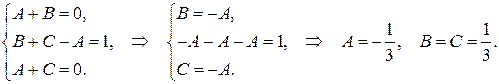
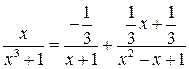 ,
, .
.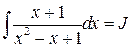 . Используя равенства
. Используя равенства ,
,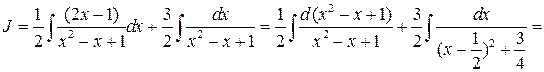
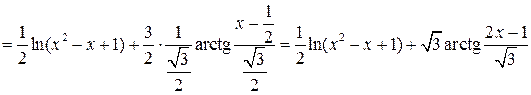 .
.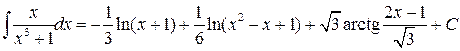 .
.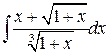 .
.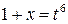 ,
, 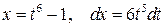 , тогда
, тогда
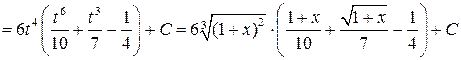 .
.


