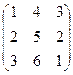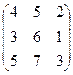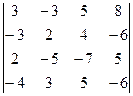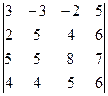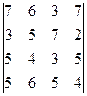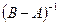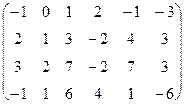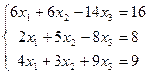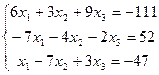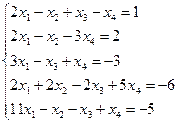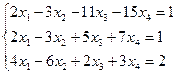Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Балансовая модель производстваСодержание книги
Поиск на нашем сайте В основе балансовой модели лежат следующие основные положения о свойствах экономической системы: 1. Экономическая система состоит из экономических объектов, причем количество продукции, выпускаемой каждым объектом, характеризуется одним числом. 2. Для выпуска данного вида продукции каждый объект получает определенное количество других видов продукции – комплектность потребления. 3. Свойство линейности: увеличение выпуска продукции в некоторое число раз требует увеличения потребления объектом других видов продукции в тоже число раз. 4. Выпускаемая каждым объектом продукция частично потребляется другими объектами, а частично поступает во вне в качестве конечной продукции данной экономической системы. Сформулированные выше предположения лишь приблизительно отражают реальную экономическую ситуацию. Но, несмотря на это, балансовые модели являются удобным инструментом планирования ввиду их простоты. 1. Пусть экономическая система состоит из n – объектов 2. Объем продукции, выпускаемой объектом 3. Конечный продукт – через 4. Через Задача состоит в составлении плана для данной экономической системы, т.е. на основании n чисел Неизвестные - локальным ограничениям, характеризующим свойства объекта; - глобальным ограничениям (требование равенства производства каждого вида продукции, потребности в ней) 1. Рассмотрим локальные ограничения свойств экономического объекта. В экономической системе, для того, чтобы охарактеризовать один экономический объект В соответствии с предположением о комплектности, требуемое количество xij определяется однозначно с помощью технологических коэффициентов aij (заданные величины)
Коэффициент aij – называется коэффициентом прямых затрат. Данным коэффициентам соответствует матрица Важной особенностью А является неотрицательность ее элементов, что запишем ее следующим образом А ³0 2. Рассмотрим глобальные ограничения. Введем следующие обозначения:
Для того чтобы объект Pj мог выпустить xj единиц продукции, он должен получить Тогда все объекты системы должны получить единиц продукции Т.к. объект Pi производит i- ый конечный продукт в объеме yi, то полный выпуск продукции объектом Pi:
Данная система уравнений (8.4.2) представляет собой систему уравнений балансовой модели и составляет модель Леонтьева. В векторно-матричном виде перепишем систему следующим образом:
В системе (8.4.3) известными являются матрица А и вектор конечной продукции Неизвестным является Для исследования системы балансовых уравнений перепишем систему (8.4.3) в следующем виде:
откуда
Т.е. необходимым и достаточным условием существования и единственности решения уравнения (8.4.3) является невырожденность матрицы Однако, исследование уравнений балансовой модели усложняется тем, что Следует отметить, что не при любой неотрицательной матрице А система балансовых уравнений имеет неотрицательное решение. Пример.
тогда система балансовых уравнений имеет вид:
Из полученного уравнения следует, что если С экономической точки зрения особый интерес представляют системы, которые имеют неотрицательные решения при любом Определение. Назовем неотрицательную матрицу А продуктивной, если существует хотя бы один такой положительный вектор С экономической точки зрения данное неравенство означает, что матрица А продуктивна, если существует такой план Сформулируем критерий продуктивности матрицы А. Неотрицательная матрица А продуктивная тогда и только тогда, когда матрица Продуктивность матрицы А является необходимым и достаточным условием существования, единственности и неотрицательности решений системы балансовых уравнений. Рассмотрим экономический смысл матрицы 1) Пусть 2) Рассмотрим частный случай вектора
Данное условие означает, что в экономической системе конечный продукт в количестве одной единицы выпускает только объект Pk, остальные объекты В этом случае Матрицу S называют матрицей полных затрат. Пример. Пусть экономическая система состоит из экономических объектов
Найти матрицу А по матрице S. Решение: 1) Матрица А определяет коэффициенты
Итак,
2)
Следует отметить, что элементы матрицы S могут быть существенно больше элементов матрицы А. Это объясняется тем, что элементы Sij указывают не только непосредственные поставки продукции объекта Pi объекту Pj, но и поставки продукции объекта Pi другим объектам для того, чтобы эти объекты могли в свою очередь поставить объекту Pj требуемые количества их продукции. Из систем балансовых уравнений следует, что планируемый орган управляющий экономической системой может определить план если точно известны элемент aij матрицы А и размеры матрицы А не слишком велики. На практике эти условия не имеют места, но при решении практических задач известны характеристики определенных объектов, т.е. информация в экономической системе рассредоточена между объектами. Поэтому при построении плана работы экономической системы необходимо согласование планов не только между отдельными экономическими объектами, но и согласование планов с планирующим органом. Назовем данную задачу задачей управления. Процедура решения задачи управления состоит из ряда шагов обмена информацией между планирующим органом и экономическими объектами. На каждом шаге планирующий орган устанавливает задание каждому объекту Pi на основании накопленной информации. После этого каждый объект сообщает планирующему органу, какое количество продукции других объектов ему необходимо для выполнения установленного задания. Планирующий орган на основании информации экономических объектов составляет новый план для каждого объекта и т.д. Назовем данную процедуру составления плана процедурой перезаказов. Пусть На первом шаге планирующий орган сообщает каждому объекту Pj в качестве задания число
Из данного выражения следует, что для составления заказов объекту Pj должны быть известны только коэффициенты aij матрицы А и yj конечной продукции. Собрав всю информацию от всех объектов, планирующий орган составляет новое задание На втором шаге планирующий орган сообщает экономическим объектам новое задание: объект Pj получает в качестве задания Сформируем следующую теорему. Теорема. Если матрица А продуктивная, то Из данной теоремы следует, что при При составлении плана методов перезаказов можно предположить, что планирующему органу не следует решать систему балансовых уравнений, т.е. не следует предварительно рассчитывать план для экономической системы. Однако на практике процедура перезаказов может включать лишь небольшое число шагов k, поэтому при небольшом числе k ошибка в определении плана может быть велика. Если же планирующий орган на основании системы балансовых уравнений получит приближенное решение, то при этом существенно уменьшится ошибка в вычислении в процедуре перезаказов. Для этого на первом шаге планирующий орган должен сообщить в качестве задания не вектор При этом, чем меньше приближенное решение отличаются от точного решения, тем меньше число шагов требуется для выполнения процедуры перезаказов. При исследовании экономической системы предполагается, что экономическим объектам требуется только продукция других объектов этой же системы. Однако, при решении практических задач должны учитываться факторы производства и потребности в продукции других экономических систем. Назовем факторы производства и потребность в продукции других систем просто факторами. Потребность экономической системы в факторах характеризуется вектором Если потребление объекта Pj в факторах обозначим через В этом случае план Следует отметить, что вектор
Ответы и указания к заданиям для самостоятельной работы Глава 1 1.1. 1.2. 1.3. 1.4. 1.5. 1.6. 1.7. а) i -ая и j -ая строки произведения поменяются местами; б) к i -ой строке произведения прибавится j -ая строка, умноженная на с; в) i -ый и j -ый столбцы произведения поменяются местами; г) к i -му столбцу произведения прибавится j -ый столбец, умноженный на с.
Глава 2 2.1. 0. 2.2. 1. 2.3. 0. 2.5. 0. 2.6. Решение. Если 2.7. Указание. Все шесть членов определителя не могут равняться +1, так как тогда произведение трех членов:
2.8. Указание. Показать, что все три положительных члена, входящих в определитель, не могут быть равны 1, и учесть, что
2.9. Указание. Смежными транспозициями перевести 1 на первое место, затем 2 на второе место и т.д. Учесть, что одна смежная транспозиция изменяет число инверсий на единицу. 2.10. 2.11. 2.12. 2.14. 2.15. 90.
Глава 3 3.1. 3.2. 3.3. 3.4. 3.5. 3.6. 3.7. 3.8. В матрице 3.9. 3.15 Указание. Используя линейное выражение всех столбцов матрицы А через столбцы, проходящие через минор d, показать, что если
Глава 4 4.1. 4.2. 4.3. 4.4. 4.5. 4.6. 4.7. 4.8. 4.9. 4.10. 4.11. Общее решение
Базисное решение
4.12. Система не совместна. 4.13. При
При и
где При
где 4.14. Общее решение
где Фундаментальная система решений
4.15. Общее решение
где Фундаментальная система решений
Глава 5 5.2. Можно добавить векторы 5.3. Например 5.4. 5.5. 3 5.7. 5.8. 5.9. 5.10. 5.11. 5.12. 5.13. 5.15. УКАЗАНИЕ. При доказательстве необходимости получить равенство В=СА, где С – невырожденная матрица из коэффициентов в выражениях системы (2) через (1). При доказательстве достаточности приписать к матрице А снизу строку координат вектора
Глава 6 6.1. 6.2. 6.3. 6.4. 6.5. 6.6. 6.7. 6.8. 6.9. 6.10. 6.14. Единственное собственное значение – 6.15.
Глава 7 7.2. 7.3. 7.4. 7.5. 7.6. 7.7. 7.8. 7.9. 7.11. Формы 7.12. Формы 7.13. 7.14. 7.15.
Контрольные задания
Контрольное задание 1 Для матриц А и В определить:
Контрольное задание 2
Вычислить определители матриц А и В:
Контрольное задание 3
Используя матрицы А и В, вычислить методом алгебраических дополнений и методом Жордана-Гусса:
Контрольное задание 4
Найти ранг матрицы двумя способами: методом окаймляющих миноров и при помощи элементарных преобразований.
Контрольное задание 5
Решить систему уравнений по формулам Крамера и матричным способом. После решения необходимо выполнить проверку.
Контрольное задание 6
Решить системы уравнений методом Жордана-Гаусса. Если система является неопределенной, то в ответ записать одно базисное решение и одно частное, не являющееся базисным.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.01 с.) |

 .
. , обозначим через
, обозначим через  .
.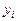 .
. обозначим ту часть продукции объекта
обозначим ту часть продукции объекта  .
. определить n 2 чисел
определить n 2 чисел  .
. необходимо указать количество продукции
необходимо указать количество продукции  других объектов
других объектов  необходимых объекту
необходимых объекту 
 , называемая матрицей прямых затрат.
, называемая матрицей прямых затрат. – вектор, характеризующий полный выпуск продукции всеми объектами.
– вектор, характеризующий полный выпуск продукции всеми объектами. – вектор, характеризующий объем продукции, идущей на конечное потребление.
– вектор, характеризующий объем продукции, идущей на конечное потребление. единиц продукции объекта
единиц продукции объекта  .
. объекта Pi.
объекта Pi. ,
, 

 .
. , которое назовем планом данной экономической системы.
, которое назовем планом данной экономической системы.

 .
.


 , то не существует неотрицательных чисел
, то не существует неотрицательных чисел 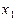 и
и  удовлетворяющих системе балансовых уравнений.
удовлетворяющих системе балансовых уравнений. . Поэтому исследование систем балансовых уравнений сводится к установлению условий, которым должна удовлетворять неотрицательная матрица А, для того чтобы существовало неотрицательное решение
. Поэтому исследование систем балансовых уравнений сводится к установлению условий, которым должна удовлетворять неотрицательная матрица А, для того чтобы существовало неотрицательное решение 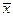 при любом
при любом 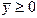 .
. .
. , что каждый объект экономической системы производит некоторое количество конечной продукции.
, что каждый объект экономической системы производит некоторое количество конечной продукции. существует и не отрицательна.
существует и не отрицательна. – j -ый столбец матрицы S, тогда
– j -ый столбец матрицы S, тогда 
 конечной продукции:
конечной продукции:
 конечной продукции не выпускают.
конечной продукции не выпускают. ,
,  , следовательно, элемент Sik равен количеству продукции, которое должен выпустить объект Pi для того, чтобы объект Pk мог выпустить одну единицу конечной продукции.
, следовательно, элемент Sik равен количеству продукции, которое должен выпустить объект Pi для того, чтобы объект Pk мог выпустить одну единицу конечной продукции. и
и  . Данные приведены в следующей таблице.
. Данные приведены в следующей таблице.






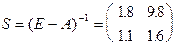
 – вектор конечного продукта, который должен произвести исследование экономической системы.
– вектор конечного продукта, который должен произвести исследование экономической системы. в ответ объект Pj сообщает планирующему органу заказы на продукцию других объектов для выполнения задания
в ответ объект Pj сообщает планирующему органу заказы на продукцию других объектов для выполнения задания 
 .
. . В ответ на полученное задание от объекта Pj поступает новый заказ, который равен
. В ответ на полученное задание от объекта Pj поступает новый заказ, который равен  и планирующим органом составляется новое задание
и планирующим органом составляется новое задание  , т.е. на k-ом шаге планирующим органом формируется задание
, т.е. на k-ом шаге планирующим органом формируется задание 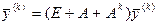 .
. .
. вектор задания
вектор задания  стремиться к вектору
стремиться к вектору  , являющемуся решением системы балансовых уравнений.
, являющемуся решением системы балансовых уравнений. , а полученное им приближенное решение
, а полученное им приближенное решение  и действовать так, как было описано выше.
и действовать так, как было описано выше. , где
, где  – потребность в i –том факторе. Числа
– потребность в i –том факторе. Числа  , то матрица
, то матрица  ,
,  ;
;  представляет собой матрицу прямых затрат факторов.
представляет собой матрицу прямых затрат факторов.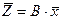 .
. , где
, где  – вектор ограничений факторов.
– вектор ограничений факторов. .
.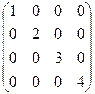 .
. при четном n,
при четном n,  при n нечетном.
при n нечетном. .
. .
. .
.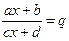 при любом х, то
при любом х, то  ,
,  ,
,  и
и  . Обратно, если
. Обратно, если  имеем
имеем  ,
, 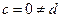 будет а= 0 и, полагая
будет а= 0 и, полагая  , снова имеем
, снова имеем  получим то же самое, полагая
получим то же самое, полагая  . Поэтому
. Поэтому  при любых х.
при любых х. ,
,  ,
,  было бы равно произведению трех остальных членов, в то время как первое из этих произведений равно произведению всех девяти элементов определителя, а второе – тому же произведению девяти элементов с противоположным знаком. Далее, убедиться, что определитель отличен от 5 и что
было бы равно произведению трех остальных членов, в то время как первое из этих произведений равно произведению всех девяти элементов определителя, а второе – тому же произведению девяти элементов с противоположным знаком. Далее, убедиться, что определитель отличен от 5 и что .
. .
. .
. .
. .
. .
.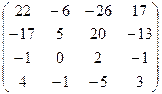 .
. .
. .
.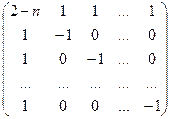 .
. .
. .
. .
. соответственно: а) поменяются местами i -ый и j -ый столбцы;
соответственно: а) поменяются местами i -ый и j -ый столбцы;  ; в) из j -го столбца вычтется i -ый, умноженный на с. При преобразовании столбцов матрицы А аналогично указанному меняются строки матрицы
; в) из j -го столбца вычтется i -ый, умноженный на с. При преобразовании столбцов матрицы А аналогично указанному меняются строки матрицы  .
. , то строки матрицы А, проходящие через d, линейно зависимы.
, то строки матрицы А, проходящие через d, линейно зависимы.











 система имеет единственное решение
система имеет единственное решение .
. общее решение
общее решение ,
,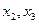 – свободные переменные.
– свободные переменные. общее решение имеет вид
общее решение имеет вид ,
, – свободная переменная.
– свободная переменная.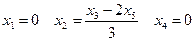 ,
, – свободные переменные.
– свободные переменные.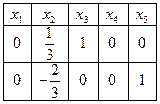
 ,
,
 .
. .
.

 равен квадрату площади параллелограмма, построенного на векторах
равен квадрату площади параллелограмма, построенного на векторах  ;
;  равен квадрату объема параллелепипеда, построенного на векторах
равен квадрату объема параллелепипеда, построенного на векторах  .
. .
. .
.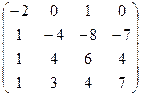 .
. .
. .
. и, вычисляя ранг методом окаймляющих миноров, показать, что ранг полученной матрицы равен k.
и, вычисляя ранг методом окаймляющих миноров, показать, что ранг полученной матрицы равен k. . Собственные векторы имеют вид
. Собственные векторы имеют вид  , где
, где  .
.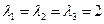 . Собственные векторы имеют вид
. Собственные векторы имеют вид 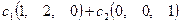 , где
, где  и
и  не равны нулю одновременно.
не равны нулю одновременно. . Собственные векторы для значения
. Собственные векторы для значения  имеют вид
имеют вид  , а для
, а для  , где
, где  . Собственные векторы имеют вид
. Собственные векторы имеют вид  , где
, где  . Собственные векторы для значения
. Собственные векторы для значения 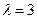 имеют вид
имеют вид  , а для
, а для  – вид
– вид  , где
, где  . Собственные векторы для значения
. Собственные векторы для значения  , а для
, а для  , где
, где  . Собственные векторы для значения
. Собственные векторы для значения  имеют вид
имеют вид  – вид
– вид  , а для
, а для  – вид
– вид  , где
, где  . Собственные векторы для значения
. Собственные векторы для значения  , а для
, а для  , где
, где  , а для
, а для  . Собственные векторы имеют вид
. Собственные векторы имеют вид  , где
, где 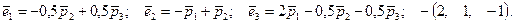
 .
. .
. .
.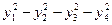 .
.



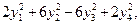

 и
и  эквивалентны между собой и не эквивалентны форме
эквивалентны между собой и не эквивалентны форме  .
.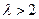 .
. .
. .
.