
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение квадратичной формыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Определение. Квадратичной формой от n неизвестных В общем виде квадратичная сумма может быть записана следующим образом:
Коэффициенты aij в этой записи образуют треугольную матрицу. Однако эта форма записи неудобна. Запишем
где Квадратичная форма может быть записана более компактно, если использовать матричные обозначения. Вынося
Таким образом, квадратичная форма в матричной записи имеет вид
где Квадратичную форму
Тогда Пример. Представить квадратичную форму
в виде скалярного произведения векторов. Решение. Очевидно, что
Тогда
7.2. Линейное преобразование переменных в квадратичной форме Пусть в квадратичной форме
В результате данного преобразования будет получена квадратичная форма, зависящая от новых переменных
Покажем, что квадратичная форма
Откуда следует симметричность матрицы Пример. Осуществить над квадратичной формой
Решение. Переменные
откуда В квадратичную форму
Определение. Квадратичная форма имеет канонический вид, если матрица С диагональна. Из данного определения следует, что квадратичная форма в каноническом виде содержит только квадраты переменных и имеет вид
Нормальным видом квадратичной формы называется сумма квадратов переменных с коэффициентами
получим Теорема. Всякая квадратичная форма может быть приведена некоторым невырожденным линейным преобразованием к каноническому виду. Доказательство. Обратимся к методу математической индукции по числу переменных. При n =1 квадратичная форма имеет канонический вид: Пусть
и пусть хотя бы один из коэффициентов
Выделим теперь в первой скобке квадрат линейной формы:
где
или
Данное преобразование задается матрицей
Так как
после которого квадратная форма
Так как
Если в квадратичной форме
После данного преобразования член
Коэффициент при Пример. Преобразовать квадратичную форму
к каноническому виду. Решение. Матрица С квадратичной формы имеет вид
Сгруппируем все члены, содержащие переменные x 1 и «выделим полный квадрат»:
Осуществим линейное преобразование переменных:
Выразим неизвестные
полученные выражения подставим в квадратичную форму. Придем к форме
Осуществляя вспомогательное преобразование
Выделим полный квадрат в квадратичной форме:
Осуществим линейное преобразование переменных:
и выразим переменные
После указанных преобразований получим квадратичную форму, зависящую от переменных
Полагая
Канонический вид квадратичной формы содержит три переменных, а не четыре. Это связано с рангом квадратичной формы. Определение. Рангом квадратичной формы называется ранг матрицы С. Теорема о приведении квадратичной формы к каноническому виду означает, что для данной симметрической матрицы С существует такая невырожденная матрица В, что Из доказательства теоремы следует, что приведение квадратичной формы к каноническому виду может осуществляться бесконечным множеством способов – например, можно сделать произвольную линейную подстановку, а затем приступить к «выделению квадратов». Поэтому матрицы В и D определяются неоднозначно. Однако число ненулевых элементов матрицы D однозначно определено и равно рангу матрицы С.
7.3. Ортогональное преобразование квадратичной формы к каноническому виду Теорема (о приведении действительной квадратичной формы к главным осям). Всякая действительная квадратичная форма Доказательство. Применим метод индукции по числу n переменных. При n =1 утверждение очевидно. Допустим, что утверждение теоремы справедливо для квадратичной формы от n -1 переменных. Рассмотрим квадратичную форму от n переменных:
Матрица преобразованной квадратичной формы есть
так как столбцы матрицы Т ортогональны и нормированы. Матрица
где Рассмотрим квадратичную форму с матрицей В. В силу индуктивного предположения найдется ортогональная матрица Q такая, что
Положим Матрица Q 1 ортогональна, так как ее первый столбец нормирован и ортогонален остальным столбцам, а остальные столбцы попарно ортогональны и нормированы в силу ортогональности матрицы Q. Тогда
Теорема доказана. Ортогональное преобразование, приводящее квадратичную форму к каноническому виду, определяется не однозначно. Однако из доказанной теоремы следует, что каково бы ни было ортогональное преобразование, приводящее к каноническому виду квадратичную форму Пример. Квадратичную форму
привести к каноническому виду. Решение. Определяем собственные значения матрицы квадратичной формы
Характеристическое уравнение имеет вид
откуда Таким образом, канонический вид квадратичной формы следующий:
Найдем ортогональное преобразование, осуществляющее приведение Решая уравнение
Преобразуя данную систему векторов в ортонормируемую систему, получим
Данная система векторов определяет ортогональную матрицу Поэтому
|
||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |

 называется алгебраическая сумма, каждый член которой является либо квадратом одного из неизвестных, либо произведением двух различных неизвестных.
называется алгебраическая сумма, каждый член которой является либо квадратом одного из неизвестных, либо произведением двух различных неизвестных.
 в следующем виде:
в следующем виде:
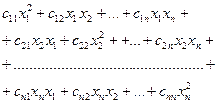
 . Такую запись квадратичной формы назовем правильной. Матрица
. Такую запись квадратичной формы назовем правильной. Матрица  называется матрицей квадратичной формы. Очевидно, что С – симметрическая матрица.
называется матрицей квадратичной формы. Очевидно, что С – симметрическая матрица. из первой строки записи,
из первой строки записи, 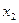 – из второй, …,
– из второй, …,  – из последней, получим
– из последней, получим

 ,
, , С – симметрическая квадратная матрица порядка n, коэффициент
, С – симметрическая квадратная матрица порядка n, коэффициент  которой равен коэффициенту при
которой равен коэффициенту при  , а коэффициент
, а коэффициент  , половине коэффициента при произведении xixj.
, половине коэффициента при произведении xixj. можно представить и в виде скалярного произведения векторов. Для этого введем
можно представить и в виде скалярного произведения векторов. Для этого введем .
. .
.
 .
. .
. делается линейное преобразование переменных
делается линейное преобразование переменных  .
. :
: .
. автоматически получается правильно записанной. Для этого достаточно убедиться в том, что матрица
автоматически получается правильно записанной. Для этого достаточно убедиться в том, что матрица  симметрична. Действительно,
симметрична. Действительно, .
. линейное преобразование, заданное матрицей
линейное преобразование, заданное матрицей .
. матрицей В преобразуются в переменные
матрицей В преобразуются в переменные  . Связь между переменными выражается матричным уравнением
. Связь между переменными выражается матричным уравнением ,
, .
. вместо переменных
вместо переменных  подставим их выражения через переменные
подставим их выражения через переменные  . Получим квадратичную форму
. Получим квадратичную форму
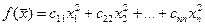 .
. . Если
. Если  , то положив
, то положив
 .
. . Допустим, что для квадратичной формы от числа переменных, меньше чем n, теорема доказана.
. Допустим, что для квадратичной формы от числа переменных, меньше чем n, теорема доказана.
 , например
, например  . сгруппируем все слагаемые, содержащие
. сгруппируем все слагаемые, содержащие 

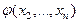 – квадратичная форма от n -1 неизвестных
– квадратичная форма от n -1 неизвестных  . Осуществим следующее преобразование:
. Осуществим следующее преобразование:

 .
. , то преобразование является невырожденным. Форма
, то преобразование является невырожденным. Форма  зависит от n -1 переменных. В силу индуктивного предположения существует невырожденное линейное преобразование D такое, что
зависит от n -1 переменных. В силу индуктивного предположения существует невырожденное линейное преобразование D такое, что
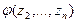 . Добавляя к преобразованию еще одну строчку, получим
. Добавляя к преобразованию еще одну строчку, получим
 , то преобразование Y=DZ невырожденное. В результате получим
, то преобразование Y=DZ невырожденное. В результате получим .
. , то в этом случае осуществим линейное преобразование:
, то в этом случае осуществим линейное преобразование: .
. преобразуется следующим образом:
преобразуется следующим образом: .
. отличен от нуля:
отличен от нуля:  . Теорема доказана.
. Теорема доказана.
 .
.

 через
через  :
: ,
, .
. , получим:
, получим: .
.

 через
через  :
: .
. .
. и выражая переменные
и выражая переменные  получим
получим .
. , где D – диагональная матрица.
, где D – диагональная матрица. – нормированный собственный вектор матрицы С, соответствующий собственному значению
– нормированный собственный вектор матрицы С, соответствующий собственному значению  . Примем
. Примем 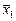 за первый столбец ортогональной матрицы
за первый столбец ортогональной матрицы .
. . Так как первый столбец матрицы Т есть собственный вектор
. Так как первый столбец матрицы Т есть собственный вектор  . Тогда
. Тогда
 симметрична, поэтому имеет вид
симметрична, поэтому имеет вид ,
, – симметричная матрица.
– симметричная матрица. .
. .
. .
. , коэффициенты этого канонического вида равны собственным числам матрицы С, причем каждое собственное число повторяется столько раз, какова его кратность как корня характеристического уравнения.
, коэффициенты этого канонического вида равны собственным числам матрицы С, причем каждое собственное число повторяется столько раз, какова его кратность как корня характеристического уравнения.
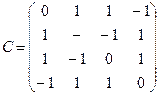 .
. ,
, .
. .
. к каноническому виду.
к каноническому виду. , найдем собственные векторы
, найдем собственные векторы
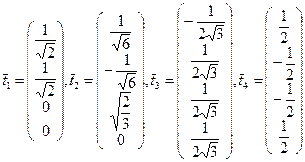 .
. преобразования переменных
преобразования переменных  . Действительно, Х=ТY, откуда
. Действительно, Х=ТY, откуда  .
.



