
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Евклидовы операторы и квадратичные формы.Содержание книги Поиск на нашем сайте
1. Что такое функционал на линейном пространстве? 2. Как построить билинейный функционал, соответствующий заданному линейному оператору? 3. Что такое сопряженные операторы? 4. Что такое самосопряженный оператор? 5. Какими свойствами обладают собственные числа самосопряженного оператора? 6. Как выглядит матрица самосопряженного оператора? 7. Что такое квадратичная форма. 8. Как по заданной квадратичной форме построить ее матрицу? 9. Какие существуют инварианты квадратичной формы. 10. Сформулировать закон инерции квадратичных форм. 11. Как записать малую и полную квадратичные формы для кривой или поверхности второго порядка, заданной своим уравнением? 12. Как инварианты квадратичной формы связаны с типом кривой или поверхности 2-го порядка?
Корни многочленов 1. Доказать, что система многочленов определенного порядка образует кольцо. 2. Что такое делитель многочлена? Привести примеры. 3. Показать на примере работу алгоритма Евклида. 4. Что такое неприводимые многочлены? 5. Сформулировать основную теорему алгебры. 6. Какова связь между общим количеством корней многочлена и их кратностью? 7. Записать формулу Кардано для корней многочлена 3-й степени. 8. Записать метод Ферарьи для нахождения корней многочлена 4-й степени. 9. Сформулировать теорему Абеля. 10. Описать основные методы приближенного нахождения действительных корней многочлена.
Рациональные дроби. 1. Что такое рациональная дробь? 2. Доказать, что множество рациональных дробей образует поле. 3. Как преобразовать неправильную рациональную дробь в сумму многочлена и правильной дроби? 4. Что такое элементарная дробь? 5. Как разложить правильную рациональную дробь в сумму элементарных дробей? 6. Сформулировать метод неопределенных коэффициентов.
Матричные многочлены и функции. 1. Что такое степень матрицы? 2. Что получится при возведении единичной матрицы в n-ю степень? 3. Записать общий вид матричного многочлена. 4. Записать общий вид матричного многочлена с числовыми коэффициентами. 5. Что такое матричный ряд? 6. Что такое сходимость матричного ряда? 7. Сформулировать достаточное условие сходимости матричного ряда. 8. Дать определение основных матричных функций. 9. Сформулировать метод приближенного нахождения матричной функции разложением по малому параметру. 10. Что такое корень матричного многочлена? 11. Что такое аннулирующий многочлен для данной матрицы? Всегда ли он существует? 12. Что такое минимальный многочлен для данной матрицы? 13. Как связаны минимальный и характеристический многочлены матрицы. 14. Сформулировать теорему Гамильтона-Кэли.
Задачи для самостоятельной работы Задачи
Задачи из данного раздела рекомендуется давать студентам в качестве домашних заданий.
БЛОК ЗАДАНИЙ № 1
БЛОК ЗАДАНИЙ №2
БЛОК ЗАДАНИЙ №3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 358; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |


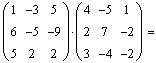
 , В=
, В=  .
.
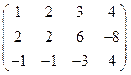 .
.
 .
.

 (0;1) и
(0;1) и  (5;1). Найти скалярное произведение
(5;1). Найти скалярное произведение 
 , если
, если  .
.
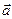 =(3;2;1),
=(3;2;1),  =(0;-1;1).
=(0;-1;1).
 , и плоскости, заданной уравнением 2x + 3y - 2z + 3 = 0.
, и плоскости, заданной уравнением 2x + 3y - 2z + 3 = 0.
 .
.
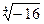

 =(1;-1;1).
=(1;-1;1).





 .
.

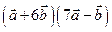
 ..
..
 .
.
 .
.




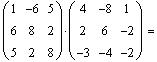
 .
.
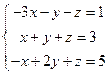

 .
.
 .
.






