
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матричные многочлены и матричные функции.Содержание книги Поиск на нашем сайте a. Определение матричного многочлена. b. Матричный многочлен с числовыми коэффициентами. c. Многочлен с матричными коэффициентами (l-матрица). d. Матричный ряд. e. Элементарные матричные функции.
a. Пусть, b. Пусть, c. Пусть, Учебно-методическое и информационное обеспечение дисциплины Основная литература 1. Данко П.Е. и др. Высшая математика в упражнениях и задачах:В 2-х томах. – М.: Высшая школа, 2008. 2. Письменный Д.Т. Конспект лекций по высшей математике: – М.: Айрис- Пресс, 2010.
Дополнительная литература 1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. Учебник для ВУЗов. – M.: Физматлит, 2007. – 308 с. 2. Беклемишев Д.В. Дополнительные главы линейной алгебры (2-е изд.). – М.: Лань, 2008. – 496 с. 3. Кострикин А.И., Манн Ю.И. Линейная алгебра и геометрия: Учебное пособие – 3 изд., стереотип. – М.: Лань 2008. – 303 с. 4. Кострикин А.И. Введение в алгебру. – М.: Физматлит, 2004. 272 с. 5. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии: Учебник для вузов. – М.: Дрофа, 2005. – 288 с. 6. Беклемишев Д.В. Дополнительные главы линейной алгебры (2-е изд.). – М.: Лань, 2008. – 496 с. 7. Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая геометрия: Учебник для вузов. Изд. 3-е, перераб. – М.: Проспект, 2007. – 400 с. 8. Каган М.Л., Самохин М.В. Математика в инженерном вузе. Алгебра и геометрия.: учебник для вузов. – М.: Озон, 2003. 9. Ван дер Варден Б.Л. Алгебра. – М.: Наука, 1976. 10. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1968. 11. Мальцев А.И. Основы линейной алгебры. – М.: Наука, 1970. 12. Проскуряков И.В. Сборник задач по линейной алгебре. – М.: Наука, 1974. 13. Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М.: Наука, 1977. 14. Рябенький В.С. Введение в вычислительную математику. – М.: Физматлит, 2000. 15. Данко П.Е. и др. Высшая математика в упражнениях и задачах. В 2-х томах. – М.: Высшая школа, 1997. 16. Рудык Б.М. и др. Общий курс высшей математики для экономистов: Учебник, М.: ИНФРА-М, 2000 г. 17. Солодовников А.С. и др. Математика в экономике: Часть 1,2,3: Учебник. – М.: Финансы и статистика, 2000-2001 гг. 18. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник для экономистов. – М.: Дело, 2001. 19. Малыхин В.И. Математика в экономике: Учебное пособие. – М.: ИНФРА-М, 2002. 20. Ермаков В.И. Сборник задач по высшей математике для экономистов: Учебное пособие. – М.: ИНФРА-М., 2002. Интернет-ресурсы 1. Справочные материалы по высшей математике http://primat.at.ua 2. Электронные учебные пособия http://book.ru-deluxe.ru
1.6. Материально-техническое обеспечение дисциплины Реализация учебной дисциплины требует наличия учебного кабинета «Линейная алгебра». Оборудование учебного кабинета: · рабочие места по количеству обучающихся; · рабочее место преподавателя; · комплект учебно-методической документации по дисциплине. Проведение лекционных и семинарских занятий предполагает использование мультимедийного оборудования: компьютера, мультимедиапроектора, интерактивной доски. Для повышения качества подготовки и оценки полученных знаний часть семинарских занятий планируется проводить в компьютерном классе с использованием математических пакетов Mathcad либо MatLab.
1.7. Методические рекомендации по изучению дисциплины Комплексное изучение предлагаемой студентам учебной дисциплины «Линейная алгебра» предполагает овладение материалами лекций, приобретение практических навыков работы при исследовании, анализе систем и моделей, выполнении индивидуальных самостоятельных заданий. Процесс по освоению всей совокупности теоретического и практического материала по дисциплине должен быть реализован в течение двух семестров и, проходить в соответствии с предложенным планом. В первом семестре изучение дисциплины "Линейная алгебра» основывается на лекционных и практических занятиях. Каждая новая тема сначала объясняется преподавателем, рассматривается на примерах, затем для закрепления полученных на занятии знаний студенты выполняют соответствующие упражнения и получают домашние задания. Полученные оценки за выполненные упражнения и домашние задания являются основой для выставления промежуточной и итоговой аттестации. Итоговой аттестацией является зачет. Зачет проводится в форме компьютерного тестирования и (или) выполнения контрольных заданий по пройденным темам. В ходе лекций раскрываются основные теоретические вопросы программы дисциплины, делаются акценты на наиболее сложные и интересные положения изучаемого материала. Материалы лекций являются базовыми для подготовки к зачету. Для закрепления полученных теоретических и практических знаний студентам в течение всего учебного года предлагаются индивидуальные задания (типовые семестровые расчеты) самостоятельной работы. Особенности выполнения самостоятельной работы и тематика индивидуальных заданий подробно изложены в методических указаниях по их выполнению. Консультирование по выполнению индивидуальных заданий может проводится через электронный обмен сообщениями, посредством Интернет. Контроль выполненных заданий осуществляется либо непосредственно на занятиях, либо на консультациях. Наличие методических рекомендаций по изучению каждой темы, большого набора заданий для самостоятельной работы по закреплению изучаемого материала (как в виде электронных заданий, так и в виде печатного сборника), компьютерных тестов для контроля знаний по каждой теме позволяет повысить эффективность учебного процесса Для подготовки к зачету студентам рекомендуются подготовленные преподавателями кафедры учебник и практикум, включающий терминологическую часть, вопросы для самоконтроля и тесты. Комплексное изучение предлагаемой студентам учебной дисциплины «Линейная алгебра» предполагает овладение материалами лекций, приобретение практических навыков для исследования, анализа и обработке информации посредством математического аппарата. Методические рекомендации по использованию дополнительной литературы Следует обратить внимание на то, что в списке дополнительной литература приведены учебные пособия более глубокого и подробного изложения материала, а также учебные пособия по отдельным главам дисциплины. Это позволит учащимся более подробно и детально изучить материал, а также поможет без особых затруднений выполнять задания для самостоятельной работы и семестровые типовые расчеты. В список дополнительной литературы вошли пособия по вопросам приложения математики в экономико-управленческой сфере. Данный аспект является необходимым для понимания применения аппарата математических разделов в будущей профессиональной сфере учащихся. 2. УЧЕБНО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
Типовые задачи. 15. Операции с векторами на плоскости. Даны векторы a. длины этих векторов; b. c. скалярное произведение данных векторов и угол между ними. 16. Операции с векторами в пространстве Даны векторы a. длины этих векторов; b. c. скалярное произведение данных векторов и угол между ними. 17. Векторное и смешанное произведение векторов. a. Определить объём параллелепипеда, построенного на векторах 18. Прямые и окружности на плоскости. a. Составить уравнение прямой, представленной на рисунке.
b. Определить угловой коэффициент "k" и величину отрезка "b", отсекаемого прямой c. Даны уравнения прямых: Какие из заданных прямых параллельны? d. Составить уравнение прямой, если известно, что прямая проходит через точку М(1;1) и имеет угловой коэффициент к=1. e. Найти длину отрезка, заключенного между точками пересечения прямой 3 у +4 х -12=0 с осями координат. f. Определить угол между прямыми х–2у–2=0 и у=–2 х+3. g. Составить уравнение прямой, проходящей через точки h. Определить, с какими из прямых а) у=3; б) у=-х; в) х=5; г) у=2х пересекается окружность х2 +у2=25. i. Определить координаты центра и радиус окружности х2 +у2 –4х+8у–16=0. j. Составить уравнение окружности, проходящей через точку М(-1;1) и центр которой лежит в точке С (-4;5). k. Определить координаты центра окружности, заданной уравнением l. Составить уравнение касательной к окружности m. Составить каноническое уравнение окружности, представленной на рисунке.
19. Кривые второго порядка. a. Определить координаты фокусов эллипса 25x2+9y2=900. b. Определить координаты фокуса и уравнение директрисы параболы х2 =4у. c. Определить, какая кривая задается уравнением: · · · · 20. Прямые, плоскости и сферы. a. Определить, какое из уравнений а) 2x-3y+z+1=0; б) x+2y-6=0; в) x+3y=0 определяет плоскость, параллельную оси OZ. b. Найти координаты нормального вектора к плоскости 2·x-3·y+z-6=0. c. Определить взаимное расположение прямых 21. Поверхности второго порядка. a. Определить, какая поверхность задаётся уравнением · · ·
22. Определители (детерминанты). Вычислить определители: a. b. c.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |

 . Найти
. Найти  с точностью до
с точностью до 
 . Найти
. Найти  с точностью до
с точностью до  . Найти
. Найти  с точностью до
с точностью до  и
и 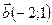 . Найти:
. Найти: ;
; и
и  . Найти:
. Найти: ;
; (1;0;1),
(1;0;1),  (4;-1;-1),
(4;-1;-1),  (1;0;1).
(1;0;1).
 на оси OY.
на оси OY. и
и  .
.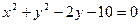 .
. в точке (3;–1).
в точке (3;–1).
 ;
; ;
; ;
; .
. и
и  .
. ;
; ;
;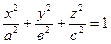 .
. ;
; ;
; .
.


