
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение двух квадратичных форм к каноническому видуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В некоторых вопросах математики и физики требуется решить следующую задачу: привести две квадратичные формы Можно показать, что эта задача не всегда имеет решение. Если же допустить дополнительно, что одна из этих форм, например Для того чтобы в этом убедиться обозначим через
Так как квадратичная форма Ранее было показано, что существует ортонормированный базис (относительно введенной нами метрики), в котором квадратичная форма принимает вид
где В этом же базисе вторая квадратичная форма
а это значит, что базис, в котором обе квадратичные формы Для того чтобы найти координаты векторов искомого базиса, рассмотрим вопрос о значениях, которые принимает квадратичная форма Квадратичная форма Задача об определении стационарных значений есть задача на условный экстремум. Для решения воспользуемся методом Лагранжа. Будем считать, что в исходном базисе квадратичные формы
В согласии с методом Лагранжа составим функцию
и приравняем нулю каждую ее частную производную по всем координатам
которая имеет ненулевые решения тогда и только тогда, когда ее определитель равен нулю, то есть
Решив уравнение (7.17), мы найдем Показано также, что коэффициенты Рассмотрим пример. Пример 1. Привести квадратичные формы
к каноническому виду и получить формулы перехода от старых координат к новым.
В нашем случае функция
Вычислим частные производные функции
Сократим каждое уравнение этой системы на 2 и запишем ее в виде
Приравняем нулю определитель этой системы
Последнее равенство можно записать в виде
или после вчисления определителя
Отсюда находим три решения:
а тогда формулы перехода от старых координат
Данные квадратичные формы имеют следующий канонический вид
Полученный результат легко проверить, если в правых частях равенств (7.18) и (7.19) заменить
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 709; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.194.29 (0.007 с.) |

 и
и  , заданные в
, заданные в  -мерном пространстве
-мерном пространстве  к каноническому (диагональному) виду и указать соответствующий базис в пространстве
к каноническому (диагональному) виду и указать соответствующий базис в пространстве 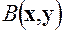 симметричную билинейную форму, соответствующую квадратичной форме
симметричную билинейную форму, соответствующую квадратичной форме  . (7.13)
. (7.13)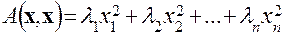 , (7.14)
, (7.14) – координаты вектора
– координаты вектора  в построенном базисе.
в построенном базисе. ,
, евклидова пространства
евклидова пространства  определенная в точках поверхности
определенная в точках поверхности 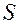 принимает в точке
принимает в точке 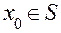 стационарное значение, если в точке
стационарное значение, если в точке 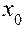 производная функции
производная функции  , соответствующего форме
, соответствующего форме  ,
, .
. (7.15)
(7.15) однородных уравнений
однородных уравнений (7.16)
(7.16) . (7.17)
. (7.17) , подставляя их последовательно в систему (7.16) мы будем находить координаты соответствующего искомого базисного вектора. Доказано, что уравнение (7.17) имеет только вещественные корни, причем каждому кратному корню соответствует столько линейно независимых решений системы (7.16) какова его кратность. Находить эти линейно независимые решения следует используя правила решения однородных систем линейных уравнений.
, подставляя их последовательно в систему (7.16) мы будем находить координаты соответствующего искомого базисного вектора. Доказано, что уравнение (7.17) имеет только вещественные корни, причем каждому кратному корню соответствует столько линейно независимых решений системы (7.16) какова его кратность. Находить эти линейно независимые решения следует используя правила решения однородных систем линейных уравнений. в канонической записи (7.14) квадратичной формы
в канонической записи (7.14) квадратичной формы  , (7.18)
, (7.18)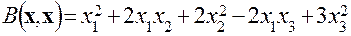 (7.19)
(7.19) будет иметь вид
будет иметь вид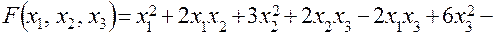
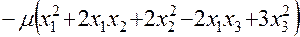 .
. и приравняем каждую из них нулю. Будем иметь
и приравняем каждую из них нулю. Будем иметь
 (7.20)
(7.20) . (7.21)
. (7.21)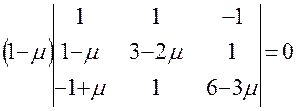
 .
. ,
,  ,
, 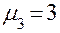 . Подставляя их в систему уравнений (7.20), находим координаты искомых базисных векторов
. Подставляя их в систему уравнений (7.20), находим координаты искомых базисных векторов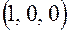 ,
, 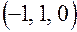 ,
,  ,
,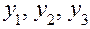 имеют вид
имеют вид ,
,  ,
,  . (7.22)
. (7.22) ,
,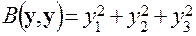 .
.


