
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несовместные системы линейных уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим несовместную систему линейных уравнений
относительно неизвестных
Подставляя различные наборы чисел Требуется найти такой набор чисел
было наименьшим по сравнению с другими возможными значениями. Заметим, что требование отыскать наименьшее значение величины (5.7) означает требование найти такие значения коэффициентов Для решения поставленной задачи введем в рассмотрение
Обозначим через
где числа
Совокупность всех линейных комбинаций (5.9) образуют подпространство
Заменив вектор
Так как поставленная задача имеет единственное решение, то определитель системы (5.11)
отличен от нуля и, следовательно, по теореме Крамера получаем выражения для коэффициентов
(5.13) Из изложенного следует, что полученный набор чисел Метод наименьших квадратов
На практике часто возникает такая задача: известно, что величина
но коэффициенты
от известных величин Пример В «Основах химии» Д.И. Менделеева приводятся экспериментальные данные о растворимости азотно-кислого натрия частей
Из теоретических соображений следует, что количественная сторона этого процесса может быть описана уравнением
где
которая несовместна. В согласии с изложенным в п. 2 введем в рассмотрение 3 вектора
а затем вычислим 5 скалярных произведений
Система уравнений (5.11) в нашем случае примет вид
решив которую получим
Если подставить в уравнение значения температуры воды из данной таблицы, то получим числа условных частей
что свидетельствует о неплохом совпадении с экспериментальными данными.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 653; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.176.238 (0.006 с.) |

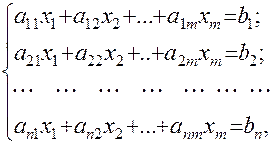 (5.6)
(5.6) . Так как система (5.6) несовместна, то это значит, что не существует такого набора чисел
. Так как система (5.6) несовместна, то это значит, что не существует такого набора чисел  , которые при подстановке в систему (5.6) вместо неизвестных
, которые при подстановке в систему (5.6) вместо неизвестных 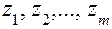 .
.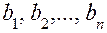 , т.е. значение выражения
, т.е. значение выражения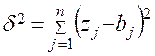 (5.7)
(5.7)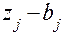 были в каком-то смысле малыми в совокупности.
были в каком-то смысле малыми в совокупности.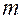 векторов
векторов 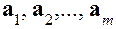 , компонентами которых являются столбцы коэффициентов при
, компонентами которых являются столбцы коэффициентов при 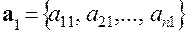 ,
, 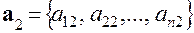 ,…,
,…, 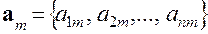 ,
,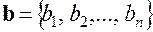 . (5.8)
. (5.8) линейную комбинацию векторов (5.8), так что
линейную комбинацию векторов (5.8), так что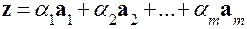 , (5.9)
, (5.9)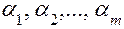 принимают любые значения.
принимают любые значения.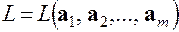 . С геометрической точки зрения ясно, что выражение (5.7) принимает наименьшее значение тогда, когда вектор
. С геометрической точки зрения ясно, что выражение (5.7) принимает наименьшее значение тогда, когда вектор  совпадает с перпендикуляром к проекциивектора
совпадает с перпендикуляром к проекциивектора 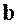 на подпространство
на подпространство  , а это значит, что вектор
, а это значит, что вектор  ;
; 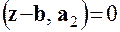 ;
; 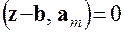 . (5.10)
. (5.10)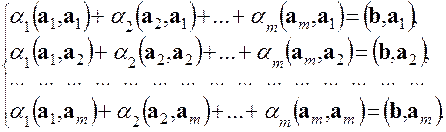 (5.11)
(5.11)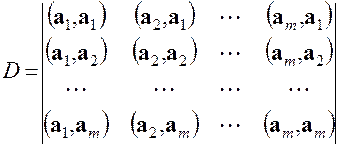 (5.12)
(5.12) ,
, 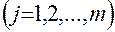
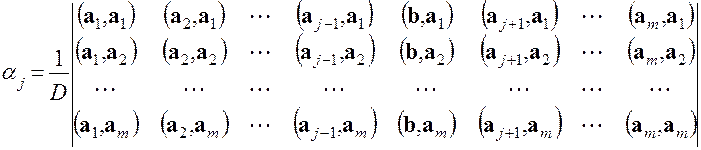
 линейно зависит от величин
линейно зависит от величин  так, что имеет место равенство
так, что имеет место равенство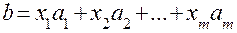 ,
, замеров (здесь
замеров (здесь 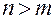 ) величины
) величины 
 . Это значит, что должны выполняться
. Это значит, что должны выполняться  ,
,  , т.е. выражение (5.7), то придем к задаче, решенной в § 2.
, т.е. выражение (5.7), то придем к задаче, решенной в § 2. в зависимости от температуры воды. В 100 частях воды растворялось следующее число условных
в зависимости от температуры воды. В 100 частях воды растворялось следующее число условных , (5.14)
, (5.14) – температура в градусах,
– температура в градусах, 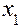 и
и 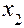 – неизвестны. Если подставить в уравнение (5.14) вместо
– неизвестны. Если подставить в уравнение (5.14) вместо  ,
,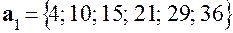 ,
, 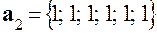 ,
,  ,
,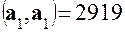 ,
, 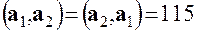 ,
, 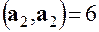 ,
, 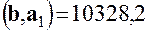 ,
,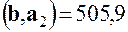 .
. ,
, ;
; 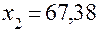 , так что искомая зависимость примет вид
, так что искомая зависимость примет вид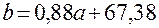 . (5.15)
. (5.15)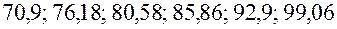 ,
,


