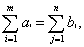Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий вид задач линейного программированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Теоретическая часть Линейное программирование Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием. Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы. Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи. Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).
Общий вид задач линейного программирования В общей постановке задача линейного программирования выглядит следующим образом: Имеются какие-то переменные х = (х1, х2, … хn) и функция этих переменных f(x) = f (х1, х2, … хn), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:
В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что Математическая модель любой задачи линейного программирования включает в себя: нахождения минимума линейной целевой функции (линейной формы) вида:
задача в которой фигурируют ограничения в форме неравенств, называется — основной задачей линейного программирования (ОЗЛП)
Задача линейного программирования будет иметь канонический вид, если в общей задаче вместо первой системы неравенств имеет место система уравнений с ограничениями в форме равенства.
Основную задачу можно свести к канонической путём введения дополнительных переменных. Задачи линейного программирования наиболее общего вида (задачи со смешанными ограничениями: равенствами и неравенствами, наличием переменных, свободных от ограничений) могут быть приведены к эквивалентным (имеющим то же множество решений) заменами переменных и заменой равенств на пару неравенств. Легко заметить, что задачу нахождения максимума можно заменить задачей нахождения минимума, взяв коэффициенты с обратным знаком.
Транспортная задача Общий вид транспортной задачи Транспортная работа - это особый класс задач линейного программирования. Задача заключается в отыскании такого плана перевозок продукции с m складов в пункт назначения n который, потребовал бы минимальных затрат. Если потребитель j получает единицу продукции (по прямой дороге) со склада i, то возникают издержки Сij. Предполагается, что транспортные расходы пропорциональны перевозимому количеству продукции, т.е. перевозка k единиц продукции вызывает расходы k С i j. Математическая модель
где xij количество продукции, поставляемое со склада i потребителю j, а С i j издержки (стоимость перевозок со склада i потребителю j). Если условие Если данное условие не выполняется, то задача называется несбалансированной или открытой и вводится либо фиктивный пункт производства, либо фиктивный пункт назначения.
Далее,
где ai есть количество продукции, находящееся на складе i, и bj - потребность потребителя j.
Таблица № 1
Будем заполнять таблицу перевозками постепенно начиная с левой верхней ячейки ("северо-западного угла" таблицы). Будем рассуждать при этом следующим образом. Пункт В1 подал заявку на 18 единиц груза. Удовлетворим эту заявку за счёт запаса 48, имеющегося в пункте А1, и запишем перевозку 18 в клетке (1,1). После этого заявка пункта В1 удовлетворена, а в пункте А1 осталось ещё 30 единиц груза. Удовлетворим за счёт них заявку пункта В2 (27 единиц), запишем 27 в клетке (1,2); оставшиеся 3 единицы пункта А1 назначим пункту В3. В составе заявки пункта В3 остались неудовлетворёнными 39 единиц. Из них 30 покроем за счёт пункта А2, чем его запас будет исчерпан, и ещё 9 возьмём из пункта А3. Из оставшихся 18 единиц пункта А3 12 выделим пункту В4; оставшиеся 6 единиц назначим пункту В5, что вместе со всеми 20 единицами пункта А4 покроет его заявку. На этом распределение запасов закончено; каждый пункт назначения получил груз, согласно своей заявки. Это выражается в том, что сумма перевозок в каждой строке равна соответствующему запасу, а в столбце - заявке. Таким образом, нами сразу же составлен план перевозок, удовлетворяющий балансовым условиям. Полученное решение является опорным решением транспортной задачи: Таблица № 2
Составленный нами план перевозок, не является оптимальным по стоимости, так как при его построении мы совсем не учитывали стоимость перевозок Сij. Другой способ - способ минимальной стоимости по строке - основан на том, что мы распределяем продукцию от пункта Ai не в любой из пунктов Bj, а в тот, к которому стоимость перевозки минимальна. Если в этом пункте заявка полностью удовлетворена, то мы убираем его из расчетов и находим минимальную стоимость перевозки из оставшихся пунктов Bj. Во всем остальном этот метод схож с методом северо-западного угла. В результате, опорный план, составленный способом минимальной стоимости по строке выглядит, так как показано в таблице № 3. При этом методе может получиться, что стоимости перевозок Cij и Cik от пункта Ai к пунктам Bj и Bk равны. В этом случае, с экономической точки зрения, выгоднее распределить продукцию в тот пункт, в котором заявка больше. Так, например, в строке 2: C21 = C24, но заявка b1 больше заявки b4, поэтому 4 единицы продукции мы распределим в клетку (2,1). Таблица № 3
Способ минимальной стоимости по столбцу аналогичен предыдущему способу. Их отличие состоит в том, что во втором способе мы распределяем продукцию от пунктов Bi к пунктам Aj по минимальной стоимости Cji. Опорный план, составленный способами минимальных стоимостей, обычно более близок к оптимальному решению. Так в нашем примере общие затраты на транспортировку по плану, составленному первым способом F0 = 1039, а по второму F0 = 723. Клетки таблицы, в которых стоят ненулевые перевозки, являются базисными. Их число должно равняться m + n - 1. Необходимо отметить также, что встречаются такие ситуации, когда количество базисных клеток меньше чем m + n - 1. В этом случае распределительная задача называется вырожденной. И следует в одной из свободных клеток поставить количество перевозок равное нулю. Так, например, в таблице № 3: m + n - 1 = 4 + 5 - 1 = 8, а базисных клеток 7, поэтому нужно в одну из клеток строки 3 или столбца 2 поставить значение “0”. Например в клетку (3,5). Составляя план по способам минимальных стоимостей в отличии от плана по способу северо-западного угла мы учитываем стоимости перевозок Cij, но все же не можем утверждать, что составленный нами план является оптимальным.
1.4 Распределительный метод оптимального плана Теперь попробуем улучшить план, составленный способом северо-западного угла. Перенесем, например, 18 единиц из клетки (1,1) в клетку (2,1) и чтобы не нарушить баланса перенесём те же 18 единиц из клетки (2,3) в клетку (1,3). Получим новый план. Подсчитав стоимость опорного плана (она ровняется 1039) и стоимость нового плана (она ровняется 913) нетрудно убедиться, что стоимость нового плана на 126 единиц меньше. Таким образом, за счёт циклической перестановки 18 единиц груза из одних клеток в другие нам удалось понизить стоимость плана:
Таблица №4
На этом способе уменьшения стоимости в дальнейшем и будет основан алгоритм оптимизации плана перевозок. Циклом в транспортной задаче мы будем называть несколько занятых клеток, соединённых замкнутой, ломанной линией, которая в каждой клетке совершает поворот на 90°. Существует несколько вариантов цикла: 1.) 2.) 3.)
Нетрудно убедиться, что каждый цикл имеет чётное число вершин и значит, чётное число звеньев (стрелок). Условимся отмечать знаком + те вершины цикла, в которых перевозки необходимо увеличить, а знаком -, те вершины, в которых перевозки необходимо уменьшить. Цикл с отмеченными вершинами будем называть означенным. Перенести какое-то количество единиц груза по означенному циклу, это значит увеличить перевозки, стоящие в положительных вершинах цикла, на это количество единиц, а перевозки, стоящие в отрицательных вершинах уменьшить на то же количество. Очевидно, при переносе любого числа единиц по циклу равновесие между запасами и заявками не меняется: по прежнему сумма перевозок в каждой строке равна запасам этой строки, а сумма перевозок в каждом столбце - заявке этого столбца. Таким образом, при любом циклическом переносе, оставляющем перевозки неотрицательными допустимый план остаётся допустимым. Стоимость же плана при этом может меняться: увеличиваться или уменьшатся. Назовём ценой цикла увеличение стоимости перевозок при перемещении одной единицы груза по означенному циклу. Очевидно, цена цикла ровна алгебраической сумме стоимостей, стоящих в вершинах цикла, причём стоящие в положительных вершинах берутся со знаком +, а в отрицательных со знаком -. Обозначим цену цикла через g. При перемещении одной единицы груза по циклу стоимость перевозок увеличивается на величину g. При перемещении по нему k единиц груза стоимость перевозок увеличиться на kg. Очевидно, для улучшения плана имеет смысл перемещать перевозки только по тем циклам, цена которых отрицательна. Каждый раз, когда нам удаётся совершить такое перемещение, стоимость плана уменьшается на соответствующую величину kg. Так как перевозки не могут быть отрицательными, мы будем пользоваться только такими циклами, отрицательные вершины которых лежат в базисных клетках таблицы, где стоят положительные перевозки. Если циклов с отрицательной ценой в таблице больше не осталось, это означает, что дальнейшее улучшение плана невозможно, то есть оптимальный план достигнут. Метод последовательного улучшения плана перевозок и состоит в том, что в таблице отыскиваются циклы с отрицательной ценой, по ним перемещаются перевозки, и план улучшается до тех пор, пока циклов с отрицательной ценой уже не останется. При улучшении плана циклическими переносами, как правило, пользуются приёмом, заимствованным из симплекс-метода: при каждом шаге (цикле) заменяют одну свободную переменную на базисную, то есть заполняют одну свободную клетку и взамен того освобождают одну из базисных клеток. При этом общее число базисных клеток остаётся неизменным и равным m + n - 1. Этот метод удобен тем, что для него легче находить подходящие циклы. Можно доказать, что для любой свободной клетке транспортной таблице всегда существует цикл и притом единственный, одна из вершин которого лежит в этой свободной клетке, а все остальные в базисных клетках. Если цена такого цикла, с плюсом в свободной клетке, отрицательна, то план можно улучшить перемещением перевозок по данному циклу. Количество единиц груза k, которое можно переместить, определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла (если переместить большее число единиц груза, возникнут отрицательные перевозки). Применённый выше метод отыскания оптимального решения транспортной задачи называется распределённым; он состоит в непосредственном отыскании свободных клеток с отрицательной ценой цикла и в перемещении перевозок по этому циклу. Распределительный метод решения транспортной задачи, с которым мы познакомились, обладает одним недостатком: нужно отыскивать циклы для всех свободных клеток и находить их цены. От этой трудоёмкой работы нас избавляет специальный метод решения транспортной задачи, который называется методом потенциалов. Метод потенциалов. Метод потенциалов является модификацией симплекс-метода решения задачи линейного программирования применительно к транспортной задаче. Он позволяет, отправляясь от некоторого допустимого решения, получить оптимальное решение за конечное число итераций. Метод потенциалов позволяет за несколько шагов (итераций) найти полностью оптимальное решение транспортной задачи. Перед решением задачи этим методом нужно найти допустимое начальное решение одним из методов, описанных в разделе выше. Вычисление потенциалов Каждому поставщику Ai соответствует потенциал Ui, а каждому потребителю Bj соответствует потенциал Vj. Данциг называет потенциалы Ui и Vj симплекс-множителями или неявными ценами. Чтобы определить эти потенциалы, полагают, что U1 =0, а остальные потенциалы вычисляют из соотношения Ui + Vj = Cij
для всех занятых (базисных) ячеек таблицы (отмечены зеленым).[3]:89
U1+V1=2. Поскольку U1=0, 0+V1=2, следовательно, V1=2 руб./кг U1+V2=3. Поскольку U1=0, 0+V2=3, следовательно, V2=3 руб./кг U2+V2=2. Поскольку V2=3, U2+3=2, следовательно, U2=–1 руб./кг U2+V3=5. Поскольку U2=–1, –1+V3=5, следовательно, V3=6 руб./кг U3+V3=2. Поскольку V3=6, U3+6=2, следовательно, U3=–4 руб./кг U3+V4=6. Поскольку U3=–4, –4+V4=6, следовательно, V4=10 руб./кг При компьютерной реализации удобно использовать рекурсию: взаимный вызов двух функций, которые отрабатывают алгоритм, соответственно, по строкам и по столбцам. Если на предыдущем шаге 4 (в разделе «Проверка плана на вырожденность») в базис была введена случайная не занятая ячейка, то вычисление u и v может дать сбой, и в этом случае случайный выбор вводимой в базис нулевой ячейки на предыдущем шаге 4 следует повторить.
Построение цикла
Допустимые циклы для транспортной задачи. Цикл перераспределения поставок представляет собой замкнутую ломаную линию, которая соединяет начальную вершину (отмечена красным цветом) и занятые (отмеченные в нашем примере зеленым цветом) ячейки транспортной таблицы по определенным правилам. 1. Все вершины, кроме начальной, находятся в занятых ячейках таблицы (ячейки с ненулевыми перевозками или «введенные в базис» на шаге 4 (в разделе «Проверка плана на вырожденность» ячейки с нулевой перевозкой — здесь они отмечены в примерах зеленым цветом), при этом охвачены циклом могут быть не все, а лишь некоторые занятые ячейки. 2. В каждой вершине цикла встречаются ровно два звена ломаной линии, причем одна из них находится по строке, а другая — по столбцу. Иначе говоря, они пересекаются под прямым углом. 3. Линия может пересекать занятые ячейки, не включая их в цикл (включение их в цикл не допускается). Другими словами, никакие три последовательные вершины не могут находиться в одной и той же строке или одном и том же столбце 4. Линия может пересекать саму себя, при этом точка пересечения не включается в цикл (исходя из п.2).
Вершины цикла в этом примере помечены звездочкой (*). Горизонтальные и вертикальные линии, соединяющие вершины, в этом примере не показаны. По вершинам цикла нужно перераспределить объемы, чтобы получить следующее приближение к оптимальному решению задачи, как это показано далее. При компьютерной реализации построения цикла удобно использовать рекурсию, то есть взаимный вызов двух функций, которые строят линии цикла по строкам и по столбцам, соответственно.
Зацикливание решения Поскольку алгоритм является циклическим (итерационным), переходим к пункту 1. Примечание: есть опасность, что алгоритм впадет в бесконечный цикл из-за вырожденности или каких-либо ошибок реализации, поэтому полезно предусмотреть проверку на максимальное число шагов или максимальное время, которое будет исполняться программа. Впрочем, по мнению Данцига, те меры, которые можно предпринять для исключения вырожденности приводят к успеху в 100 % случаев. Для подстраховки можно применить метод Фогеля, который не склонен «впадать» в бесконечные циклы, и выдает более или менее приближенное к оптимальному решение за ограниченное число шагов.
Теоретическая часть Линейное программирование Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием. Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы. Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи. Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).
Общий вид задач линейного программирования В общей постановке задача линейного программирования выглядит следующим образом: Имеются какие-то переменные х = (х1, х2, … хn) и функция этих переменных f(x) = f (х1, х2, … хn), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:
В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что Математическая модель любой задачи линейного программирования включает в себя: нахождения минимума линейной целевой функции (линейной формы) вида:
задача в которой фигурируют ограничения в форме неравенств, называется — основной задачей линейного программирования (ОЗЛП)
Задача линейного программирования будет иметь канонический вид, если в общей задаче вместо первой системы неравенств имеет место система уравнений с ограничениями в форме равенства.
Основную задачу можно свести к канонической путём введения дополнительных переменных. Задачи линейного программирования наиболее общего вида (задачи со смешанными ограничениями: равенствами и неравенствами, наличием переменных, свободных от ограничений) могут быть приведены к эквивалентным (имеющим то же множество решений) заменами переменных и заменой равенств на пару неравенств. Легко заметить, что задачу нахождения максимума можно заменить задачей нахождения минимума, взяв коэффициенты с обратным знаком.
Транспортная задача
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 5268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.048 с.) |

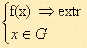
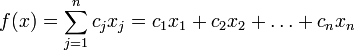
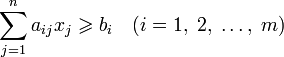 ,
,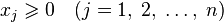 .
.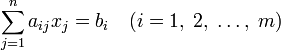 ,
,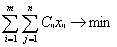
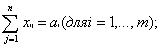

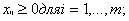
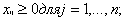
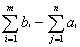 равны, то транспортная задача называется сбалансированной т. е. закрытой.
равны, то транспортная задача называется сбалансированной т. е. закрытой.