
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулировка транспортной задачиСодержание книги
Поиск на нашем сайте Пусть Задача формулируется как найти при условиях где
Матрица ограничений транспортной задачи состоит из столбцов Алгоритм Метод потенциалов является модификацией симплекс-метода, в котором базисная матрица Двойственные переменные симплекс-метода для транспортной задачи называются потенциалами. Потенциалы Для дуги Таким образом, потенциал потребителя равна потенциалу производителя + стоимость перевозки. С экономической точки зрения это можно трактовать как стоимость продукта в точке потребления. Проверка оптимальности плана Добавление дуги приводит к возникновению цикла в дереве. Увеличение провоза по вводимой дуге приводит к пересчету потоков в цикле, провоз по одной из дуг при этом уменьшится до нуля. Дугу с нулевым потоком удаляем из базиса, при этом базисный граф остается деревом (цикл разрывается). Остается только пересчитать потенциалы — добавить (или вычесть — зависит от направления дуги) ко всем вершинам «повисшей ветки» величину невязки Процесс завершается, когда для всех дуг условие оптимальности
Алгоритм решения метода потенциалов Эта проверка не входит в алгоритм метода потенциалов, но может потребоваться для исключения арифметических ошибок (при ручном расчете на бумаге) или самопроверки алгоритма при компьютерных вычислениях. Особенностью распределения груза по транспортной таблице является совпадение суммы объемов по строкам с запасами соответствующего поставщика, а суммы объемов по столбцам — с потребностями соответствующих потребителей. В показанном выше примере, § Для 1-й строки: 30 кг = 20 + 10 кг § Для 2-й строки: 40 кг = 20 + 20 кг § Для 3-й строки: 20 кг = 10 + 10 кг § Для 1-го столбца: 20 кг = 20 кг § Для 2-го столбца: 30 кг = 10 + 20 кг § Для 3-го столбца: 30 кг = 20 + 10 кг § Для 4-го столбца: 10 кг = 10 кг Вычисление общей стоимости транспортировки Этот шаг также не входит в сам алгоритм метода потенциалов, но он полезен для распечатки результатов и показа, что алгоритм движется в правильном направлении, уменьшая на каждом (или не на каждом) шаге общую себестоимость перевозки. Для всех ячеек цена умножается на объем перевозки и полученный результат суммируется.
В нашем примере, сумма затрат на перевозку груза составляет 2×20 + 3×10 + 2×20 + 5×20 + 2×10 + 6×10 = 290 руб.
Разделение ячеек на базисные и свободные Ячейки (клетки) транспортной таблицы с ненулевыми перевозками называются базисными, а клетки с нулевыми объемами перевозки — свободными.
1.5.5 Проверка плана на вырожденность Базисных (см. выше) ячеек таблицы должно быть не менее m+n-1, где m и n — соответственно, число поставщиков и потребителей, иначе решение считается вырожденным и требует введения в базис одной из ячеек с нулевой перевозкой(чтобы алгоритм не впал в бесконечный цикл, эта ячейка должна быть случайной). Для исключения ситуаций с вырожденностью к объемам потребления добавляют небольшие возмущения — числа, заведомо ничтожные при перевозках (такие как 0.00001), при этом к объему поставки одного из поставщиков добавляют их сумму (или наоборот).
Вычисление потенциалов Каждому поставщику Ai соответствует потенциал Ui, а каждому потребителю Bj соответствует потенциал Vj. Данциг называет потенциалы Ui и Vj симплекс-множителями или неявными ценами. Чтобы определить эти потенциалы, полагают, что U1 =0, а остальные потенциалы вычисляют из соотношения Ui + Vj = Cij
для всех занятых (базисных) ячеек таблицы (отмечены зеленым).[3]:89
U1+V1=2. Поскольку U1=0, 0+V1=2, следовательно, V1=2 руб./кг U1+V2=3. Поскольку U1=0, 0+V2=3, следовательно, V2=3 руб./кг U2+V2=2. Поскольку V2=3, U2+3=2, следовательно, U2=–1 руб./кг U2+V3=5. Поскольку U2=–1, –1+V3=5, следовательно, V3=6 руб./кг U3+V3=2. Поскольку V3=6, U3+6=2, следовательно, U3=–4 руб./кг U3+V4=6. Поскольку U3=–4, –4+V4=6, следовательно, V4=10 руб./кг При компьютерной реализации удобно использовать рекурсию: взаимный вызов двух функций, которые отрабатывают алгоритм, соответственно, по строкам и по столбцам. Если на предыдущем шаге 4 (в разделе «Проверка плана на вырожденность») в базис была введена случайная не занятая ячейка, то вычисление u и v может дать сбой, и в этом случае случайный выбор вводимой в базис нулевой ячейки на предыдущем шаге 4 следует повторить.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 666; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.007 с.) |

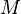 — пункты производства/потребления,
— пункты производства/потребления, 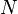 — дуги перевозок,
— дуги перевозок, 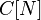 — цены провоза по дугам
— цены провоза по дугам 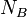 — набор базисных столбцов.
— набор базисных столбцов.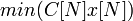
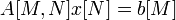
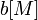 — производство (+) / потребление (-)
— производство (+) / потребление (-)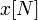 — решение
— решение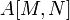 , содержащих всего два ненулевых элемента — +1 для производителя и −1 для потребителя.
, содержащих всего два ненулевых элемента — +1 для производителя и −1 для потребителя.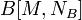 представлена в виде дерева.
представлена в виде дерева.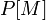 вычисляются по формуле
вычисляются по формуле 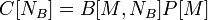 , что эквивалентно
, что эквивалентно 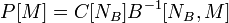
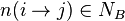 потенциалы дуг связаны формулой
потенциалы дуг связаны формулой 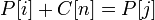 .
.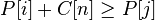 легко трактуется с экономической точки зрения — если стоимость продукта в точке потребления больше стоимости в точке производства + цена перевоза, по этой дуге следует везти. Величина
легко трактуется с экономической точки зрения — если стоимость продукта в точке потребления больше стоимости в точке производства + цена перевоза, по этой дуге следует везти. Величина 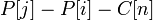 называется невязкой дуги.
называется невязкой дуги.


