
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к выполнению задачСодержание книги Поиск на нашем сайте
Методические указания к выполнению задач
Содержание
1. МОДЕЛИ ЗАДАЧ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ 1.1. Задача об оптимальном распределении ресурсов при выпуске продукции на предприятии (об ассортименте) 1.2. Задача о смесях (рационе, диете) 1.3. Транспортная задача 1. 4. Модель рационального использования посевных площадей 1. 5. Модель рационального использования имеющихся мощностей 1.6. Задача о закреплении самолетов за воздушными линиями 1.7. Задача о ранце 1.8. Задача о назначениях 1.9. Задача коммивояжера 1.10. Задача о доставке (покрытии множества) 2. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ПОМОЩЬЮ EXCEL 2.1. Ввод условий задачи 2.2. Работа в диалоговом окне "Поиск решения" 3. ПРИМЕРЫ РЕШЕНИЯ ОПТИМИЗАЦИОННЫХ ЗАДАЧ СРЕДСТВАМИ EXCEL 3.1. Получение требуемого сплава 3.2. Транспортная задача 3.3. Рациональное использование имеющихся площадей 3.4. Рациональное использование технологических участков 3.5. Закрепление самолетов за воздушными линиями 3.6. Задача о ранце 3.7. Назначение механизмов на работы 3.8. Задача коммивояжера 3.9. Задача о доставке 4. ВАРИАНТЫ ЗАДАНИЙ
Модели задач математического программирования
Задача об оптимальном распределении ресурсов при выпуске продукции на предприятии (об ассортименте)
Предположим, что предприятие выпускает n различных изделий. Для их производства требуются m различных видов ресурсов (сырья, вспомогательных материалов, рабочего и машинного времени и т.д.). Эти ресурсы ограничены и составляют в планируемый период b1, b2,..., bm условных единиц. Известны также технологические коэффициенты aij, которые указывают, сколько единиц i-го ресурса требуется для производства изделия j-го вида (i= Пусть прибыль, получаемая предприятием при реализации единицы изделия j-го вида, равна cj. В планируемый период все показатели bi, aij и cj предполагаются постоянными. Требуется составить такой план выпуска продукции, при реализации которого прибыль предприятия была бы наибольшей.
Сведем данные условия задачи в таблицу:
Допустим, что предприятие будет выпускать xi изделий вида i. Требуется составить оптимальный план работы предприятия X={xj}, j=
Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
Целевая функция (ЦФ) представляет суммарную прибыль. Ограничения имеют вид:
Xj³ 0, j= Уравнения ограничений модели представляют собой ограничения задачи по объему соответствующего ресурса, в ходе выполнения плана можно использовать либо весь запас этого ресурса либо часть его.
Транспортная задача
Требуется составить план перевозок однородного груза таким образом, чтобы общая стоимость перевозок была минимальной. Исходная информация: ai- количество единиц груза в i- м пункте отправления(i= bj- потребность в j- м пункте назначения (j= cij- стоимость перевозки единицы груза из i- го пункта в j- й. Обозначим через xij планируемое количество единиц груза для перевозки из i-го пункта в j- й. В принятых обозначениях:
В простейшем случае должны выполняться следующие условия:
Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарную стоимость перевозок. Ограничения имеют вид:
xij³ 0, i= Согласно уравнениям ограничений модели количество вывезенного груза должно быть равно количеству принятого.
Задача о ранце
Здесь речь идет о собравшемся в поход путешественнике, который должен упаковать в ранец различные полезные предметы n наименований, причем могут потребоваться несколько одинаковых предметов. Имеются m ограничений такого типа, как вес, объем, линейные размеры и т.д. Пусть аij- i-я характеристика предмета j-го наименования i=
Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарная полезность собранных предметов. Ограничения имеют вид:
xj³ 0, xj- целое, j= Условия (1) означают, что количество отобранных предметов не превышает возможностей погрузки. Данная задача является задачей линейного целочисленного программирования.
Задача о назначениях
Имеется n работников, которых требуется назначить на n работ. Известно, что j-ю работу i-й работник будет выполнять с эффективностью cij. Требуется так распределить работников, чтобы максимизировать суммарную эффективность. Положим xij=1, если i-й работник назначен на j-ю работу; xij=0, в противном случае, i, j= Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарную эффективность. Ограничения имеют вид:
xij равно либо 0, либо 1. Условия (1) означают, что каждый работник назначается только на одну работу. Условия (2) означают, что один работник выполняет только одну работу. Данная задача является задачей линейного булева программирования.
Задача коммивояжера
Имеется n городов. Выезжая из исходного города А1, коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город А1. Задача заключается в определении последовательности объезда городов при которой коммивояжеру требуется минимизировать некоторый критерий эффективности: стоимость проезда, время в пути, суммарное расстояние и т.д. Пусть задана матрица C=||cij|| расстояний между городами и требуется минимизировать суммарную длину пути. Введем переменные xij=1, если коммивояжер переезжает из города Аi в город Аj, i¹ j; xij=0, в противном случае, i, j= Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарную длину пути. Ограничения имеют вид:
ui-uj+(n-1)× xij £ n-2, 2£ i¹ j £ n, (3) где ui, i= Условия (1) означает, что коммивояжер выезжает из каждого города один раз, а условия (2)- что он въезжает один раз в каждый город. Условия (3), выглядящие несколько искусственно, предназначены обеспечить связность маршрута коммивояжера. Более точно эти условия запрещают любой цикл, не проходящий через город 1, и тем самым исключают ситуации, подобные приведенной на рисунке.
1 2 5 6
Данная задача является задачей линейного булева программирования.
1.10. Задача о доставке (покрытии множества)
Фирма обслуживает некоторое количество клиентов (m). Каждый день она доставляет своим клиентам товары на грузовых машинах (или по железной дороге, воздушным путем, на баржах и т.д.). Существует множество допустимых маршрутов (n) доставки, каждый из которых позволяет обслужить определенное подмножество клиентов и требует использования в течении дня одного транспортного средства. Каждый маршрут характеризуется определенными расходами, которые могут соответствовать его длине, или стоимости расходуемого топлива и т.д. Цель состоит в том, чтобы выбрать такое множество маршрутов, при котором обеспечивается обслуживание каждого из клиентов, каждый клиент обслуживается один раз в день и суммарные расходы минимальны.
Введем переменные: xj=1, если маршрут j выбран; xj=0, в противном случае, j= Обозначим элементы aij следующим образом: aij=1, если i-й клиент обслуживается по маршруту j; aij=0, в противном случае, i= Обозначим стоимость доставки по маршруту j через сj. Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарные расходы доставки по выбранным маршрутам. Ограничения имеют вид:
Согласно условиям (1) каждый клиент обслуживается один раз в день. Данная задача является задачей линейного булева программирования.
Ввод условий задачи
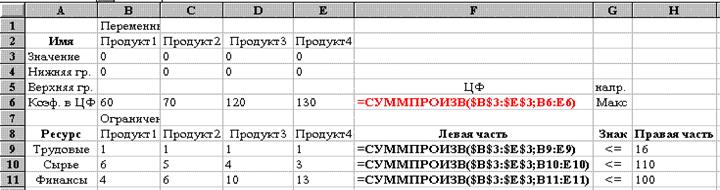
Ввод условий задачи состоит из следующих основных шагов: 1). Создание формы для ввода условий задачи. 2). Ввод исходных данных (коэффициентов математической модели). 3). Ввод целевой функции, ограничений и граничных условий. Последовательность работ рассмотрим на примере задачи распределения ресурсов. Фирма выпускает продукцию четырех типов Продукт1, Продукт2, Продукт3, Продукт4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Норма расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в табл., там же приведено наличие располагаемого ресурса. Требуется определить, в каком количестве надо выпускать продукцию каждого типа, чтобы суммарная прибыль была максимальной.
Составим математическую модель, для чего введем следующие обозначения: xj- количество выпускаемой продукции j-го типа j=1,2,3,4; bi- количество располагаемого ресурса i-го вида i=1,2,3; aij- норма расхода i-го ресурса для выпуска единицы продукции j-го типа; cj- прибыль, получаемая от реализации единицы продукции j-го типа. Из табл. видно, что для выпуска единицы Продукта1 требуется 6 единиц сырья, значит, для выпуска всей продукции первого типа требуется 6x1 единиц сырья, где x1- количество выпускаемой продукции Продукт1. С учетом того, что для других видов продукции зависимости будут аналогичны, ограничение по сырью будет иметь вид:
6× x1+5× x2+4× x3+3× x4 £ 110. В этом ограничении левая часть равна величине требуемого ресурса, а правая показывает количество имеющегося ресурса. Аналогично можно составить ограничения для остальных ресурсов и написать зависимость для целевой функции. Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид: 60× x1+70× x2+120× x3+130× x4® max Ограничения имеют вид: x1+x2+x3+x4£ 16 6× x1+5× x2+4× x3+3× x4£ 110 4× x1+6× x2+10× x3+13× x4£ 100 xj³ 0; j=
Рис. 6 1). Форма ввода условий задачи представлена на рис. 6. Весь текст на рисунке (и в дальнейшем) является комментарием и на решение задачи не влияет. 2). Необходимые исходные данные приведены на рис. 7.
Рис. 7 3). Рассмотрим алгоритмы ввода уравнений целевой функции и ограничений: · Установить курсор в ячейку, содержащую целевую функцию (F6).
Рис. 8 Следует отметить, что во все диалоговые окна адреса ячеек удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести. · В массив 2 ввести B6:E6.
Рис. 9 В ячейке F6 отображается значение целевой функции, оно равно 0. Ввод ограничений (в ячейки F9, F10, F11) осуществляется аналогичным образом, с заданием соответствующих адресов. Однако значительно проще можно выполнить данную процедуру используя мышь. Для этого подведите курсор мыши к ячейке с целевой функцией (F6), нажмите клавишу <Ctrl> (при этом рядом с изображением курсора мыши должен появиться знак "+"). Удерживая <Ctrl> перетащите содержимое ячейки F6 в ячейку F9. Содержимое F6 скопировано в F9. Ячейка F9 стала активной, об этом свидетельствует черная рамка вокруг нее, также называемая курсором. В правом нижнем углу курсора-рамки имеется маленький квадрат. Подведите курсор мыши к нему (курсор мыши превратится в черный крестик), "ухватите" мышью квадрат и тяните вниз до ячейки F11 включительно. Таким образом вы скопируете формулу из F9 в ячейки F10 и F11. Теперь таблица примет вид, представленный на рис. 10. В режиме представления формул она показана на рис. 11.
Рис. 10
Рис. 11 Все необходимые условия внесены в таблицу в виде формул. Следующим этапом будет поиск решения задачи средствами Excel.
2.2. Работа в диалоговом окне "Поиск решения"
1). Выберите последовательно опции меню Сервис, Поиск решения. На экране появится соответствующее окно (рис. 12).
Рис. 12 Поясним смысл элементов окна. Установить целевую ячейку- определяет целевую ячейку, значение которой необходимо максимизировать или минимизировать, или сделать равным конкретному значению. Изменяя ячейки- определяет изменяемые ячейки. Изменяемая ячейка- это ячейка, которая может быть изменена в процессе Поиска Решения для достижения нужного результата в ячейке из окна Установить целевую ячейку с удовлетворением поставленных ограничений.
Предположить- отыскивает все неформульные ячейки, прямо или непрямо зависящие от формулы в окне Установить целевую ячейку, и помещает их ссылки в окно Изменяя ячейки. Ограничения- перечисляет текущие ограничения в данной проблеме. Добавить- выводит окно диалога “Добавить ограничение”, в котором можно добавить ограничения к текущей проблеме. Изменить- выводит окно диалога “Изменить ограничение”, в котором можно модифицировать имеющиеся ограничения. Удалить- удалить выделенное ограничение. Выполнить- запускает процесс решения определенной проблемы. Закрыть- закрывает окно диалога, не решая проблемы. Сохраняются лишь изменения, сделанные при помощи кнопок Параметры, Добавить, Изменить и Удалить. Не сохраняются изменения, произведенные после использования данных кнопок. Параметры- выводит окно диалога “Параметры поиска решения”, в котором можно контролировать различные аспекты процесса отыскания решения, а также загрузить или сохранить некоторые параметры, такие, как выделение ячеек и ограничений, для какой-то конкретной проблемы на рабочем листе. Восстановить- очищает все текущие установки проблемы и возвращает все параметры к их значениям по умолчанию. Курсор ввода с клавиатуры установлен в поле Установить целевую ячейку. Сюда необходимо внести адрес ячейки, содержащей целевую функцию. Для того чтобы сделать это щелкните мышью на той ячейке рабочего листа, где содержится ЦФ (F6). Вокруг F6 появился движущийся пунктирный контур, а в поле окна- соответствующий адрес. Следует отметить, что подобным способом можно вносить все остальные необходимые данные, это удобнее, чем вводить их с клавиатуры. 2). В поле Равной выберите флажок Максимальному значению. 3). Введите адреса искомых переменных, для этого выделите мышью область таблицы B3:E3. 4). Ввод ограничений задачи. Щелкните на кнопке Добавить. На экране появилось окно "Добавление ограничения" (рис. 13). Excel воспринимает ограничения в виде ссылок на ячейки в которых содержатся соответствующие формулы, при этом левая часть ограничения представляет собой, как правило, ссылку на формулу, а правая- значение: число или ссылку на ячейку, содержащую значение. Адреса ячеек должны содержать символ $. Если определяется интервал ячеек, то он должен быть той же формы и тех же размеров, что и интервал в окне Ссылка на ячейку. Некоторые из ограничений примера представлены на рис. 12.
Рис. 13 Ссылка на ячейку- определяет ячейку или интервал ячеек, чьи значения необходимо ограничить. Ограничение- определяет условие, налагаемое на содержимое окна Ссылка на ячейку. Выберите из списка отношение, которое нужно установить между ячейкой или интервалом и ограничением, которое нужно ввести в окне справа от списка. Можно выбрать <=, =, >=, или "цел". Если Вы выбрали "цел" для указания на то. что переменная должна быть целочисленной, то слово "Целое" появляется в окне справа от списка. Добавить- в окне диалога “Добавить ограничение” можно добавить новое ограничение без возврата в диалог “Параметры поиска решений”. Если при вводе задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делается с помощью кнопок Изменить, Удалить (рис. 12). На этом ввод условий задачи закончен. 5). Установка параметров решения. Щелкните мышью по кнопке Параметры. На экране появится окно "Параметры поиска решения" (рис. 14). С помощью команд, находящихся в этом окне можно вводить условия для решения задач оптимизации всех классов. Позволяет контролировать различные аспекты процесса отыскания решения, загрузить или сохранить такие параметры, как ссылки на ячейку и ограничения для конкретной проблемы на рабочем листе. Можно определять параметры для линейных и нелинейных задач. Каждый из параметров в окне диалога имеет значение по умолчанию, подходящий для большинства проблем.
Рис. 14 Поясним элементы окна. Максимальное время- ограничивает время, требующееся для процесса отыскания решения. Это значение должно быть положительным целым числом. Значение по умолчанию равно 100 (секунд), что вполне годится для большинства малых задач, хотя Вы можете ввести любое значение до 32767. Число итераций- ограничивает время, требующееся для процесса отыскания решения, путем ограничения числа промежуточных вычислений. Это значение должно быть положительным целым числом до 32767. Точность- контролирует точность ответов, получаемых при поиске решений. Число, вводимое в поле Точность: · используется при определении того, удовлетворяет ли значение ячейки ограничения нужному равенству или находится ли оно в указанных границах.
указывает на меньшую точность, если число введено с меньшим количеством десятичных знаков; например, 0,0001. Вообще говоря, чем большая точность определяется (чем меньше число), тем больше времени понадобится для поиска решения. Методы, используемые Поиском Решения, позволяют существенно ускорить поиск, если установить исходное значение, достаточно близкое к искомому решению. Допустимое отклонение- проблемы, связанные с изменяемыми ячейками, которые должны содержать целые значения, могут требовать большого количества времени, так как при этом необходимо решать несколько подпроблем, каждая из которых есть задача для Поиска Решений с целочисленными ограничениями. Можно подобрать величину отклонения, которая представляет процент допустимого отклонения от оптимального решения при целочисленных ограничениях для всех элементов задачи. Чем выше отклонение (допустимое отклонение в процентах), тем быстрее процесс решения. Установка отклонения не играет роли, если не введены целочисленные ограничения. Линейная модель- ускоряет процесс отыскания решения. Команда может быть использована только, если все связи в модели линейны. Показать результаты итераций- прерывает Поиск Решения и показывает результаты после каждой итерации. Автоматический масштаб- включает автоматический масштаб. Это полезно, когда параметры ввода (Изменяя ячейки) и вывода (Установить целевую ячейку и Ограничения) сильно различаются по величине; например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей. Оценка- эти флажки определяют подход, используемый для получения исходных оценок основных переменных в каждом одномерном поиске. · линейная- использует линейную экстраполяцию вдоль касательного вектора.
Производная- параметры группы Производная определяют способ вычисления производной при оценке частных производных целевых и ограничивающих функций. Эти варианты существенно отличаются своим действием на функциях, чье графическое представление недостаточно гладко или непрерывно. Для таких функций следует использовать вариант Центральная. · прямая- такой способ дифференцирования установлен по умолчанию.
Метод- параметры метод определяют, какой алгоритм поиска используется при каждой итерации для направления поиска. Нужно указать либо метод Ньютона, либо метод сопряженного градиента. · метод Ньютона- это метод поиска по умолчанию, использующий квази-ньютоновский подход. Этот метод обычно требует больше памяти, чем метод сопряженного градиента, но меньшее количество итераций.
Загрузить модель- выводит окно диалога "Загрузить Модель", в котором можно указать, какую именно модель нужно загрузить. Сохранить модель- выводит окно диалога "Сохранить Модель", в котором можно указать, где именно нужно сохранить данную модель. Используйте кнопку Сохранить модель только в том случае, если нужно сохранить более, чем одну модель Поиска Решения вместе с данным рабочим листом. Первая модель Поиска Решений автоматически сохраняется вместе с рабочим листом. Установите флажок Линейная модель, остальные параметры будем использовать по умолчанию. 6). Нажмите OK, затем кнопку Выполнить в окне "Поиск решения". Через некоторое время на экране появится окно "Результаты поиска решения" (рис. 15).
Рис. 15 Окно диалога "Результаты поиска решения" выводит результаты последнего вычисления, используя значения ячеек, наиболее близкие к нужному решению. Когда Поиск Решения завершает попытки отыскания решения, то на экран в верху окна диалога "Результаты поиска решений" выводится сообщение о завершении. Сохранить найденное решение- принимает решение, найденное Поиском Решения, и подставляет найденные значения в соответствующие ячейки. Восстановить исходные значения- восстанавливает исходные значения в изменяемых ячейках. Сохранить сценарий- открывает окно диалога Сохранить сценарий, в котором можно сохранить данную проблему для использования Диспетчером Сценариев пакета Microsoft Excel. Отчеты- создает указанный тип отчета. Каждый отчет появляется на отдельном листе рабочей книги. · Результаты- перечисляет изменяемые ячейки и ячейку в окне Установить целевую ячейку вместе с исходным и конечным значением. Также показывает ограничения и информацию о них.
Результаты поиска появятся в таблице (рис. 16).
Рис. 16 На рис. 16 видно, что в оптимальном решении Продукт1=B3=10; Продукт2=C3=0; Продукт3=D3=6; Продукт4=E3=0. При этом максимальная прибыль будет составлять F6=1320, а количество использованных ресурсов равно: трудовых=F9=16, сырья=F10=84, финансов=F11=100. Таково оптимальное решение рассматриваемой задачи распределения ресурсов. Однако решение задачи находится не всегда. Если условия задачи несовместны, на экране появится диалоговое окно (рис. 17):
Рис. 17 Если целевая функция неограничена, то на экране появится диалоговое окно (рис. 18):
Рис. 18
Примеры решения оптимизационных задач средствами Excel
Получение требуемого сплава
Предприятию требуется изготовить некоторое количество сплава, содержащего не менее 15 компонент олова, 55 компонент цинка и 30 компонент свинца. Требуемый сплав изготавливается из трех исходных сплавов, в которых содержатся вышеуказанные составляющие. Данные о содержании олова, цинка и свинца в исходных материалах приведены в таблице, там же задана стоимость единицы каждого сплава. Следует определить, какие из исходных сплавов и в каких количествах нужно использовать для получения требуемого сплава, чтобы суммарные затраты на исходные сплавы были минимальными.
Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид: 5× x1+4× x2+7× x3® min, Ограничения имеют вид: 40× x1+30× x2+25× x3=30 40× x1+60× x2+45× x3=55 20× x1+10× x2+30× x3=15 xj³ 0, j= Вид электронной таблицы Excel, созданной для решения задачи, представлен на рис. 19. Поясним содержание некоторых ячеек таблицы. В блоке ячеек В3:D3 находятся искомые значения xj, которые до выполнения поиска решения были равны 0. Адрес данного блока входит в поле ввода Изменяя ячейки в окне “Поиск решения” (см. рис. 21). Ячейки блока выполняют роль переменных целевой функции и ограничений- xj.
Рис. 19 Блок ячеек B4:D4 содержит правые части граничных неравенств (граничных условий). В ячейках блока содержатся нулевые значения (см. рис. 19). Блок ячеек B6:D6 содержит данные о цене единицы исходных материалов, каждая его ячейка играет роль коэффициента при целевой функции в математической модели. В блоках ячеек B10:D12 и G10:G12 находятся данные, соответствующие коэффициентам aij и bi ограничений математической модели.
Рис. 20 Сами формулы целевой функции и ограничений расположены соответственно в ячейке E6 и ячейках E10, E11, E12 (см. рис. 19 и 20). Вид электронной таблицы в режиме отображения формул представлен на рис. 20. После ввода условий задачи необходимо перейти к поиску решения, инициировав соответствующее диалоговое окно (см. рис. 21). Данные в окно удобно вводить с помощью мыши. Для этого необходимо установить курсор в соответствующее поле ввода, затем выделить на рабочем листе требуемые ячейки, адреса выбираемых ячеек автоматически будут появляться в поле ввода. Обычно в поле ввода Изменяя ячейки (см. рис. 21) заносятся адреса ячеек, которые выполняют роль переменных математической модели. Таким образом, под x1, x2, x3 отводятся ячейки B3, C3, D3. Ограничения удобно задавать поблочно. Первое ограничение данного примера (см. рис. 21) представляет собой запись граничных условий, в которой каждая ячейка левого блока больше либо равна каждой ячейке правого блока. Левый блок означает, как известно, совокупность переменных xj, правый- множество нижних границ переменных. В данном примере нижней границей всех xj является 0, поэтому можно было бы записать: $B$3:$D$3>=0. Вторая запись в группе Ограничения представляет три ограничения по содержанию требуемых компонентов в сплаве. В каждой ячейке левого блока содержится формула одного из ограничений (см. рис. 20), ячейки правого блока содержат требования bi. По-прежнему, знак “>=“ относится каждой ячейке обоих блоков.
Рис. 21 Способ задания ограничений поблочно существенно облегчает ввод однотипных ограничений. Так, для данного примера двумя записями были заданы шесть ограничений. Результаты поиска решения заносятся в ячейки таблицы (см. рис. 19). Прежде всего это значения xj. Для получения требуемого сплава нужно 0,44 единицы сплава1 и 0,63 единиц сплава2. Стоимость нового сплава равна 46,88 д. е., количество компонент свинца, цинка и олова равно соответственно 36,25; 55; 15 компонент.
Транспортная задача
Три поставщика одного и того же продукта располагают в планируемый период следующими запасами этого продукта: первый- 120 условных единиц, второй- 100 и третий 80 единиц. Этот продукт должен быть перевезен к трем потребителям, спросы которых соответственно равны 90, 90 и 120 условных единиц. Приведенная ниже таблица содержит показатели затрат, связанных с перевозкой продукта из i-го пункта отправления в j-й пункт потребления. Требуется перевезти продукт с минимальными затратами.
Математическая модель задачи выглядит следующим образом. Целе
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.66.147 (0.019 с.) |

 j=
j=  ).
). ® max.
® max. , i=
, i=  ,
,
 - общая (суммарная) стоимость перевозок;
- общая (суммарная) стоимость перевозок; =ai - количество груза, вывозимого из i- го пункта;
=ai - количество груза, вывозимого из i- го пункта; =bj - количество груза, доставляемого в j- й пункт.
=bj - количество груза, доставляемого в j- й пункт. , i=
, i=  .
.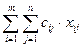 ® min.
® min. , j=
, j=  ® max.
® max. i=
i=  ® max.
® max. , j=
, j= 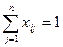 , i=
, i=  , j=
, j=  - неограниченные действительные переменные.
- неограниченные действительные переменные. 4 3 7
4 3 7


 =1, i=
=1, i=  .
.

 -Мастер функций (на панели инструментов). На экране: диалоговое окно "Мастер функций шаг 1 из 2" (рис. 8).
-Мастер функций (на панели инструментов). На экране: диалоговое окно "Мастер функций шаг 1 из 2" (рис. 8). 









 .
.





