
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели задач математического программированияСодержание книги Поиск на нашем сайте
Задача об оптимальном распределении ресурсов при выпуске продукции на предприятии (об ассортименте)
Предположим, что предприятие выпускает n различных изделий. Для их производства требуются m различных видов ресурсов (сырья, вспомогательных материалов, рабочего и машинного времени и т.д.). Эти ресурсы ограничены и составляют в планируемый период b1, b2,..., bm условных единиц. Известны также технологические коэффициенты aij, которые указывают, сколько единиц i-го ресурса требуется для производства изделия j-го вида (i= Пусть прибыль, получаемая предприятием при реализации единицы изделия j-го вида, равна cj. В планируемый период все показатели bi, aij и cj предполагаются постоянными. Требуется составить такой план выпуска продукции, при реализации которого прибыль предприятия была бы наибольшей.
Сведем данные условия задачи в таблицу:
Допустим, что предприятие будет выпускать xi изделий вида i. Требуется составить оптимальный план работы предприятия X={xj}, j= Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
Целевая функция (ЦФ) представляет суммарную прибыль. Ограничения имеют вид:
Xj³ 0, j= Уравнения ограничений модели представляют собой ограничения задачи по объему соответствующего ресурса, в ходе выполнения плана можно использовать либо весь запас этого ресурса либо часть его.
Задача о смесях (рационе, диете)
К группе задач о смесях относят задачи по отысканию наиболее дешевого набора из определенных исходных материалов, обеспечивающих получение смеси с заданными свойствами. Иными словами, получаемые смеси должны иметь в своем составе n различных компонентов в определенных количествах, а сами компоненты являются составными частями m исходных материалов.
Обобщенная таблица задачи о смесях выглядит следующим образом.
Коэффициенты aij показывают удельный вес i-го компонента в единице j-го материала. Обозначим через xj количество материала j-го вида, входящего в смесь. Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарную стоимость смеси. Ограничения имеют вид:
где bi- минимально необходимое содержание i-й компоненты в смеси. xj³ 0, j= Условия (1) представляют собой ограничения задачи по содержанию компонент в смеси, смесь должна содержать компоненты в объемах, не менее указанных.
Транспортная задача
Требуется составить план перевозок однородного груза таким образом, чтобы общая стоимость перевозок была минимальной. Исходная информация: ai- количество единиц груза в i- м пункте отправления(i= bj- потребность в j- м пункте назначения (j= cij- стоимость перевозки единицы груза из i- го пункта в j- й. Обозначим через xij планируемое количество единиц груза для перевозки из i-го пункта в j- й. В принятых обозначениях:
В простейшем случае должны выполняться следующие условия:
Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарную стоимость перевозок. Ограничения имеют вид:
xij³ 0, i= Согласно уравнениям ограничений модели количество вывезенного груза должно быть равно количеству принятого.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.84.207 (0.007 с.) |

 j=
j=  ).
). ® max.
® max. , i=
, i=  ,
,
 , i=
, i=  - общая (суммарная) стоимость перевозок;
- общая (суммарная) стоимость перевозок; =ai - количество груза, вывозимого из i- го пункта;
=ai - количество груза, вывозимого из i- го пункта; =bj - количество груза, доставляемого в j- й пункт.
=bj - количество груза, доставляемого в j- й пункт. , i=
, i=  .
.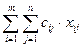 ® min.
® min. , j=
, j= 


