Назначение механизмов на работы

 

Имеются три механизма М₁, М₂, М₃, каждый из которых может быть использован на трех видах работ Р₁, Р₂, Р₃ с производительностью (в условных единицах), заданной в виде таблицы:

Механизмы	Работы
	Р1	Р2	Р3
М1
М2
М3

Требуется так распределить механизмы по одному на каждую из работ, чтобы суммарная производительность всех механизмов была максимальной.

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

x₁₁+2× x₁₂+3× x₁₃+2× x₂₁+4× x₂₂+x₂₃+3× x₃₁+x₃₂+5× x_33® max,

Ограничения имеют вид:

x₁₁+x₁₂+x₁₃=1,

x₂₁+x₂₂+x₂₃=1,

x₃₁+x₃₂+x₃₃=1,

x₁₁+x₂₁+x₃₁=1,

x₁₂+x₂₂+x₃₂=1,

x₁₃+x₂₃+x₃₃=1.

Вид электронной таблицы Excel, созданной для решения задачи, представлен на рис. 37. Значения переменных x_ij располагаются в блоке ячеек B4:D6 (см. рис. 37). Коэффициенты целевой функции, отражающие производительность механизмов, находятся по адресам B11:D13.

Рис. 37

Формулы целевой функции и ограничений находятся соответственно в ячейке E8 и ячейках E4:E6 (каждый механизм может быть назначен только на одну работу), B8:D8 (каждая работа выполняется только на одном механизме) (см. рис. 37 и 38). Вид электронной таблицы в режиме отображения формул представлен на рис. 38.

Рис. 38

Рис. 39

Данная задача является задачей линейного булева программирования и в ней переменные x_ij должны принимать значения либо 0 либо 1. В поиске решения такое ограничение задается тремя ограничениями, по которым изменяемые ячейки в блоке (x_ij) одновременно больше либо равны 0, меньше либо равны 1 и являются целыми. Первые три записи в группе Ограничения (см. рис. 39) отражают этот факт.

Результаты поиска решения приведены на рис. 37.

 

Задача коммивояжера

 

Коммивояжеру, находящемуся в Париже, необходимо посетить три города. Он получил информацию о стоимости проезда самолетом в каждый из выбранных городов и стоимость проезда из одного города в другой. На основе добытых данных он составил матрицу стоимостей (см. табл.) проезда в выбранные города и обратно. Зная матрицу стоимостей коммивояжеру надо так составить маршрут путешествия, чтобы затраты на путешествие были бы минимальными и чтобы выполнялось требование: каждый пункт посещается только один раз.

 

 

Пункты	Париж	Берлин	Рим	Лондон
Париж
Берлин
Рим
Лондон

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

0x₁₁+270× x₁₂+430× x₁₃+160× x₁₄+70× x₂₁+0× x₂₂+160x₂₃+10x₂₄+200× x₃₁+130x₃₂+0× x₃₃+ +350× x₃₄+210× x₄₁+160x₄₂+250× x₄₃+0× x_44® min,

Ограничения имеют вид:

x₁₁+x₂₁+x₃₁+x₄₁=1,

x₁₂+x₂₂+x₃₂+x₄₂=1,

x₁₃+x₂₃+x₃₃+x₄₃=1.

x₁₄+x₂₄+x₃₄+x₄₄=1,

x₁₁+x₁₂+x₁₃+x₁₄=1,

x₂₁+x₂₂+x₂₃+x₂₄=1,

x₃₁+x₃₂+x₃₃+x₃₄=1,

x₄₁+x₄₂+x₄₃+x₄₄=1,

u₂-u₃+3× x_23£ 2,

u₂-u₄+3× x_24£ 2,

u₃-u₂+3× x_32£ 2,

u₃-u₄+3× x_34£ 2,

u₄-u₂+3× x_42£ 2,

u₄-u₃+3× x_43£ 2.

Вид электронной таблицы, созданной для решения задачи, представлен на рис. 40. Значения переменных x_ij располагаются в блоке B3:E6. В данном блоке ячейки, расположенные по диагонали обнулены (пункт назначения не может быть одновременно пунктом прибытия) и выделены, для удобства задания ограничений. Даны стоимости проезда из города в город (блок B11:E14). Для вычислений необходимо задать размерность задачи n (количество городов)- ячейка F16.

Рис. 40

Целевая функция расположена в ячейке F8. Ограничения находятся в блоках B7:E7 (коммивояжер въезжает один раз в каждый город) и F3:F6 (коммивояжер выезжает из каждого города один раз) (см. рис. 40 и 41). Вид электронной таблицы в режиме отображения формул представлен на рис. 41. В задаче коммивояжера есть ряд специфических ограничений по дополнительным переменным u_i (см. мат модель). Формулы этих ограничений находятся в блоке ячеек B17:E19. Значения самих переменных располагаются в блоке B8:E8.

На рис. 42 представлена запись условий задачи в окне "Поиск решения". Как известно, дополнительные переменные не относятся к целевой функции, но они, также как и x_ij, являются изменяемыми, поэтому адреса содержащих их ячеек должны быть введены в поле Изменяя ячейки одновременно с адресами переменных целевой функции.

Операцию ввода удобно проводить с помощью мыши. Необходимо установить курсор ввода в поле Изменяя ячейки, затем выделить мышью блок ячеек переменных целевой функции, нажать <Ctrl> и, удерживая эту клавишу, выделить мышью блок ячеек рабочего листа, отведенный для переменных u_i. В поле ввода адреса блоков отделяются ";" (см. рис. 42).

Рис. 41

Перечислим ограничения, которых не видно на рис. 42: $C$4=0; $D$5=0; $E$6=0; $F$3:$F$6=1.

Рис. 42

Первая запись в группе Ограничения представляет собой совокупность ограничений по дополнительным переменным u_i. Каждая ячейка блока в левой части неравенства содержит формулу одного ограничения (см. рис. 41 и мат. модель), правую часть представляет одно значение, равное n-2, содержащееся в F18. Такая запись означает, что каждая ячейка блока $B$17:$D$19 меньше либо равна 2 (4-2=2).

В поиске решения нельзя явно задать ограничение i¹ j. Исходя из смысла переменных x_ij можно предположить, что значения тех x_ij, для которых i=j (расположенных по диагонали в блоке переменных), всегда должны быть равны 0 и ввести соответствующие ограничения. В группе Ограничения таких ограничений четыре: $B$3=0, $C$4=0, $D$5=0, $E$6=0.

По результатам поиска решения найден ответ задачи: из Парижа коммивояжер летит в Лондон, оттуда в Рим, затем в Берлин, откуда возвращается в Париж. Общая стоимость перелета составит 610 д. е. (см. рис. 40).

 

Задача о доставке

 

Фирма обслуживает 5 клиентов. Каждый день она доставляет своим клиентам товары на грузовых машинах. Существует 3 допустимых маршрута доставки, каждый из которых позволяет обслужить определенное количество клиентов и требует использования в течении дня одного транспортного средства. Каждый маршрут характеризуется определенными расходами (см. табл.). Необходимо выбрать такое множество маршрутов, при котором обеспечивается обслуживание каждого из клиентов и, кроме того, суммарные расходы минимальны, при условии, что каждый клиент обслуживается один раз в день.

Таблица обслуживания клиентов по маршрутам
Клиенты	Маршруты
Расходы по маршруту

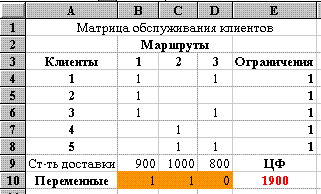
Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

900× x₁+1000× x₂+800× x_3® min,

Ограничения имеют вид:

1× x₁₁+0× x₂₁+1× x₃₁=1,

1× x₁₂+0× x₂₂+0× x₃₂=1,

1× x₁₃+0× x₂₃+1× x₃₃=1,

0× x₁₂+1× x₂₂+0× x₃₂=1,

0× x₁₃+1× x₂₃+1× x₃₃=1.

Вид электронной таблицы Excel, созданной для решения задачи, представлен на рис. 43. Значения переменных x_j располагаются в блоке ячеек B10:D10 (см. рис. 43). Коэффициенты целевой функции, отражающие стоимость доставки по маршруту, находятся по адресам B9:D9. Данные об обслуживании клиентов по маршрутам имеются в блоке B4:D8

Рис. 43

Формулы целевой функции и ограничений находятся соответственно в ячейке E10 и ячейках E4:E8 (каждый клиент обслуживается по каждому маршруту только один раз в день) (см. рис. 43 и 44). Вид электронной таблицы в режиме отображения формул представлен на рис. 44.

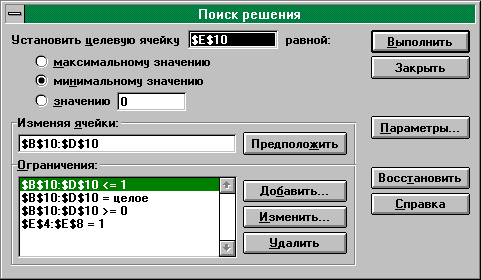
Рис. 44

Запись условий задачи в окне "Поиск решения" можно увидеть на рис. 45.

Результаты поиска решения приведены на рис. 43.

Рис. 45

 

 

Варианты заданий

 

В приводимых ниже задачах требуется по словесному описанию составить экономико-математическую модель задать исходные данные и получить результат средствами Microsoft Excel.

 

4.1. Завод выпускает изделия двух типов: А и В. При этом используется сырье четырех видов. Расход сырья каждого вида на изготовление единицы продукции и запасы сырья заданы следующей таблицей:

Изделия	Сырье
	I	II	III	IV
А
B
Запасы сырья

Выпуск одного изделия типа А приносит 3 денежные единицы прибыли, одного изделия типа В- 2 денежные единицы. Составить план выпуска продукции, обеспечивающий наибольшую прибыль.

4.2. На заводе используется сталь трех марок: А, В и С, запасы которых соответственно равны 10, 16, и 12 ед. Завод выпускает два вида изделий. Для изделия I требуется по одной единице стали всех марок. Для изделия II требуется 2 единицы стали марки В, одна- марки С и не требуется сталь марки А. От реализации единицы изделия вида I завод получает 300 руб. прибыли, вида II- 200 руб. Составить план выпуска продукции, дающий наибольшую прибыль.

4.3. Предприятие располагает ресурсами двух видов в количестве 120 и 80 ед. соответственно. Эти ресурсы используются для выпуска продукции I и II, причем расход на изготовление единицы продукции первого вида составляет 2 ед. ресурса первого вида и 2 ед. ресурса второго вида, единицы продукции второго вида- 3 ед. ресурса первого вида и 1 ед. ресурса второго вида. Прибыль от реализации единицы продукции первого вида составляет 600 руб., второго вида- 400 руб. Составить план выпуска продукции, обеспечивающий наибольшую прибыль, при условии, что продукции первого вида должно быть выпущено не менее продукции второго вида.

4.4. Фабрика выпускает три вида тканей. Суточные ресурсы фабрики следующие: 700 ед. производственного оборудования, 800 ед. Сырья и 900 ед. электроэнергии, расход которых на единицу ткани представлен в таблице.

Ресурсы	Ткани
	I	II	III
Оборудование
Сырье
Электроэнергия

Цена одного метра ткани I равна 8 руб., ткани II- 7 и ткани III- 6 руб. Сколько надо произвести ткани каждого вида, чтобы прибыль от реализации была наибольшей?

4.5. Четыре станка обрабатывают два вида деталей: А и В. Каждая деталь проходит обработку на всех четырех станках. Известны: время обработки детали на каждом станке, время работы станков в течении одного цикла производства и прибыль, получаемая от выпуска одной детали каждого вида. Эти данные приведены в таблице.

 

 

Станки	Время обработки одной детали, ч.	Время станка за один цикл производства, ч.
	A	B
I
II
III
IV
Прибыль на одну деталь, руб.

Составить план производства, обеспечивающий наибольшую прибыль.

4.6. Для откорма животных употребляют два корма: 1 и 2. Стоимость одного килограмма корма 1- 5 руб., корма 2- 2 руб. В каждом килограмме корма 1 содержится 5 ед. витамина А, 2,5 ед. витамина В и 1 ед. витамина С. В каждом килограмме корма 2 содержится 3 ед. витамина А, 3 ед. витамина В и 1 ед. витамина С.

Какое количество корма каждого вида необходимо расходовать ежедневно, чтобы затраты на откорм были минимальными, если суточный рацион предусматривает не менее 225 питательных единиц витамина А, не менее 150 ед. витамина В и не менее 80 ед. витамина С?

4.7. На птицеферме употребляется два вида кормов- I и II. В единице веса корма I содержится единица вещества А, единица вещества В и единица вещества С. В единице веса корма II содержатся четыре единицы вещества А, две единицы вещества В и не содержится вещество С. В дневной рацион каждой птицы надо включить не менее единицы вещества А, не менее четырех единиц вещества В и не менее единицы вещества С. Цена единицы веса корма I составляет 30 руб., корма II- 20 руб. Составить ежедневный рацион кормления птицы так, чтобы обеспечить наиболее дешевый рацион питания.

4.8. На трех станциях отправления А, В и С имеется соответственно 50, 20 и 30 ед. однородного груза, который нужно доставить в пять пунктов назначения П₁, П₂, П₃, П₄, П₅ в количестве соответственно 30, 5, 25, 15 и 25 ед. Эти данные, а также стоимость перевозки единицы груза от каждой станции отправления к каждому пункту назначения указаны в таблице.

Пункты	Запасы	Пункты назначения и их потребности
отправления	груза	П1	П2	П3	П4	П5
А
В
С

Составить такой план перевозок грузов, чтобы затраты на эти перевозки были минимальными.

4.9. Даны условия транспортной задачи. Числа, находящиеся на пересечении строк с указанием мощностей поставщиков и столбцов с указанием спроса потребителей, показывают стоимость перевозки единиц груза от поставщиков к потребителям.

 

 

Пункты	Запасы	Пункты назначения и их потребности
отправления	груза
I
II
III
IV

Составить такой план перевозок грузов, чтобы затраты на перевозки были минимальными.

4.10. Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков приведено в таблице.

Станок	Время обработки одного изделия, ч.
	Тип 1	Тип 2	Тип 3	Тип 4

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость одного машино-часа составляет 10 долл. для станка 1 и 15 долл.- для станка 2. Допустимое время использования станков ограничено следующими значениями: 500 машино-часов- для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1, 2, 3 и 4 равны 65, 70, 55 и 45 долл. соответственно. Сформулируйте для приведенных условий задачу максимизации суммарной чистой прибыли.

4.11. Завод выпускает изделия трех моделей (I, II и III). Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют 4000 и 6000 единиц. Расход ресурсов на одно изделие каждой модели приведен в таблице.

Ресурс	Расход ресурса на одно изделие данной модели
	I	II	III
A
В

Трудоемкость изготовления изделия модели I вдвое больше, чем изделия модели II, и втрое больше, чем изделия модели III. Численность рабочих завода позволяет выпускать 1500 изделий модели I. Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I, II и III соответственно. Однако соотношение выпуска изделий моделей I, II и III должно быть равно 3:2:5. Удельные прибыли от реализации изделий моделей I, II и III составляют 30, 20 и 50 долл. соответственно. Сформулируйте для данных условий задачу определения объемов выпуска изделий каждой модели, при которых прибыль будет максимальной.

4.12 Денежные средства могут быть использованы для финансирования двух проектов. Проект А гарантирует получение прибыли в размере 70 центов на вложенный доллар через год. Проект В гарантирует получение прибыли в размере 2 долл. на каждый инвестированный доллар, но через два года. При финансировании проекта В период инвестиций должен быть кратным двум годам. Как следует распорядится капиталом в 100 000 долл., чтобы максимизировать суммарную величину прибыли, которую можно получить через три года после начала инвестиций? Сформулируйте задачу ЛП.

4.13 Минимально необходимое количество автобусов в i-й час суток равно b_i, i=1, 2,..., 24. Каждый автобус используется на линии в течении 6 час. Превышение числа автобусов в период i по сравнению с величиной b_i приводит к дополнительным издержкам на один машино-час в размере c_i. Сформулируйте данную задачу как задачу минимизации общей величины дополнительных издержек.

4.14. Дано распределения самолетов трех типов по четырем маршрутам. Характеристики парка самолетов и движения по авиалиниям приведены в таблице.

Тип самолета	Вместимость (число пассажиров)	Колич. cамолетов	Количество рейсов в сутки на каждом маршруте
Суточный пассажиропоток

 

Тип самолета	Эксплуатационные расходы на 1 рейс по данному маршруту, долл.
Убыток от неудовлетворенного спроса (на одного неперевезенного пассажира)

Необходимо так распределить самолеты по авиалиниям, чтобы суммарные эксплуатационные расходы были минимальны.

4.15. Для получения двух сплавов А и В используются четыре металла I, II, III и IV. Требования к содержанию этих металлов в сплавах А и В приведены ниже.

Сплав	Требования к содержанию металлов
А	Не более 80% металла I Не более 30% металла II Не менее 50% металла IV
В	От 40 до 60% металла II Не менее 30% металла III Не более 70% металла IV

Характеристики и запасы руд, из которых получаются металлы I, II, III и IV, указаны в таблице.

 

 

Руда

Максимальный

Состав, %

Цена, долл./т

запас, т

I

II

III

IV

Другие компоненты

Пусть цена 1 т сплава А равна 200 долл., а 1 т сплава В- 300 долл. Сформулируйте задачу ЛП, в которой требуется максимизировать прибыль от продажи сплавов А и В.

4.16. Фирма производит две модели А и В сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 3 м². досок, а для изделия В- 4 м². Фирма может получить от своих поставщиков до 1700 м². досок в неделю. Для каждого изделия модели А требуется 12 мин. машинного времени, а для изделия модели В- 30 мин. В неделю можно использовать 160 ч. машинного времени. Сколько изделий каждой модели следует выпускать в неделю, если каждое изделие модели А приносит 2 ден. ед. прибыли, а каждое изделие модели В- 4 ден. ед. прибыли?

4.17. Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч. в сутки. Время обработки и прибыль от продажи одного изделия приведены в таблице. Найдите оптимальные объемы производства изделий каждого вида.

Изделие	Время обработки 1 изделия, мин.	Удельная прибыль
	Станок 1	Станок 2	Станок 3
				2 долл.
				3 долл.

4.18. Фирма имеет возможность рекламировать свою продукцию, используя местные радио- и телевизионную сети. Затраты на рекламу в бюджете фирмы ограничены величиной 1000 долл. в месяц. Каждая минута радиорекламы обходится в 5 долл., а каждая минута телерекламы в 100 долл. Фирма хотела бы использовать радиосеть по крайней мере в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определите оптимальное распределение финансовых средств, ежемесячно отпускаемых на рекламу, между радио- и телерекламой.

4.19. Фирма планирует рекламную кампанию нового продукта. Отведенный на эти цели бюджет составляет 120 000 руб. Предполагается, что тираж рекламных объявлений должен составить не менее 800 млн. экземпляров; объявления будут размещены в шести изданиях: Издание1, Издание2,..., Издание6. Каждое издание имеет свой тираж(см. табл.). Фирма подсчитала стоимость размещения рекламы в одном выпуске издания (см. табл.). необходимо распространить рекламу с минимальными издержками при следующих дополнительных ограничениях:

a). В каждом издании реклама должна пройти в шести или более выпусках.

б). На любое издание может быть истрачено не более одной трети отпущенной суммы.

в). Общая стоимость рекламы в третьем и четвертом изданиях не должна превышать 75 000 руб.

 

№ Изд.	Стоимость размещения рекламы в одном выпуске издания (руб.)	Тираж одного выпуска (млн.)
	1474,2	9,9
	1244,1	8,4
		8,2
	700,7	5,1
		3,7
	524,4	3,6

4.20. Фирма рекламирует свою продукцию с использованием четырех средств: телевизора, радио, газет и афиш. Из различных рекламных экспериментов, которые проводились в прошлом, известно, что эти средства приводят к увеличению прибыли соответственно на 10, 3, 7 и 4 ден. ед. в расчете на 1 ден. ед., затраченную на рекламу.

Распределение рекламного бюджета по различным средствам подчинено следующим ограничениям:

а) полный бюджет не должен превосходить 500 000 ден. ед.;

б) следует расходовать не более 40 % бюджета на телевидение и не более 20 % бюджета на афиши;

в) вследствие привлекательности для подростков радио на него следует расходовать по крайней мере половину того, что планируется на телевидение.

Сформулируйте задачу распределения средств по различным источникам как задачу линейного программирования и решите ее.

4.21. Фирма производит два вида продукции- А и В. Объем сбыта продукции вида А составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 фунтов. Расход сырья на единицу продукции А составляет 2 фунта, а на единицу продукции В- 4 фунта. Цены продукции А и В 20 и 40 долл. соответственно. Определите оптимальное распределение сырья для изготовления продукции А и В.

4.22. Фирма производит два продукта А и В, рынок сбыта которых неограничен. Каждый продукт должен быть обработан каждой из машин I, II, III. Время обработки в часах для каждого из изделий приведено ниже:

	I	II	III
A	0,5	0,4	0,2
В	0,25	0,3	0,4

Время работы машин I, II, III соответственно 40, 36 и 36 ч. в неделю. Прибыль от изделий А и В составляет соответственно 5 и 3 долл. Фирме надо определить недельные нормы выпуска изделий А и В, максимизирующие прибыль. Сформулируйте эту задачу как задачу линейного программирования и решите ее.

4.23. Фирме требуется уголь с содержанием фосфора не более 0,03% и долей зольных примесей не более 3,25%. Три сорта А, В, С, доступны по следующим ценам (за одну т.):

 

Сорт угля	Содержание примеси фосфора, %	Содержание примесей золы, %	Цена, долл.
A	0,06	2,0
B	0,04	4,0
С	0,02	3,0

Как их смешивать, чтобы получить минимальную цену и удовлетворить ограничения на содержания примесей?

4.24. Средства очистки пола оценены по трем параметрам:

а) очищающие свойства,

б) дезинфицирующие свойства,

в) Раздражающее воздействие на кожу.

Продукт на рынке должен иметь по крайней мере 60 ед. очищающих свойств и по крайней мере 60 ед. дезинфицирующих свойств по соответствующей шкале. При этом раздражающее воздействие на кожу должно быть минимальным. Конечный продукт должен быть смесью трех основных очистителей, характеристики которых приводятся в таблице.

Очиститель	Очищающие свойства	Дезинфицирующие свойства	Раздражающее воздействие на кожу
A
B
С

Сформулируйте задачу нахождения оптимальной смеси, как задачу линейного программирования.

4.25. Фирма производит два продукта А и В, продаваемых соответственно по 8 и 15 центов за упаковку; рынок сбыта для каждого из них практически не ограничен. Продукт А обрабатывается на машине 1, продукт В- на машине 2. Затем оба упаковываются на фабрике (см. рис.). 1 кг. сырья стоит 6 центов; машина 1 обрабатывает 5000 кг. в 1 ч. с потерями 10%. Машина 2 обрабатывает 400 кг. в 1 ч. и с потерями 20%. Машина 2 доступна 5 ч. в день и ее использования стоит 336 долю в 1 ч. Упаковка продукта А весит 1/4 кг., а упаковка продукта В- 1/3 кг. Фабрика может работать 10 ч. в день, производя в 1 ч. продукции стоимостью 3600 долл. За 1 ч. можно упаковать 12000 продуктов А и 8000 продуктов В.

Компания хочет определить такие объемы потребления сырья продуктов А и В (в тыс. кг.), при которых дневная прибыль максимальна. Сформулируйте задачу линейного программирования и решите ее.

4.26. В некоторой местности в двух пунктах А и В имеется потребность в дополнительном транспорте. В пункте А требуется 5 дополнительных автобусов, а в пункте В- 7. Известно, что 3, 4, 5 автобусов могут быть получены соответственно из гаражей G1, G2, G3.

Как следует распределить эти автобусы между пунктами А и В, чтобы минимизировать их суммарный пробег? Расстояния от гаражей до пунктов А и В приведены в таблице:

Гараж	Расстояния до пунктов
	А	В
G1
G2
G3

4.27. Компания производит полки для ванных комнат двух размеров А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м². материала, а для полки типа В- 3 м². материала в неделю. Для изготовления 1 полки типа А требуется 12 мин. машинного времени, а для изготовления одной полки типа В- 30 мин.; можно использовать 160 ч. машинного времени в неделю. Если прибыль от продажи полок типа А составляет 3 долл., а от полок типа В- 4 долл., то сколько полок каждого типа следует выпускать в неделю?

4.28. Автозавод выпускает 2 модели: “Каприз” и (более дешевую) “Фиаско”. На заводе работает 1000 неквалифицированных и 800 квалифицированных рабочих, каждому из которых оплачивается 40 ч. в неделю Для изготовления модели “Каприз” требуется 30 ч. неквалифицированного и 50 ч. квалифицированного труда; “Фиаско” требуется 40 ч. неквалифицированного и 20 ч. неквалифицированного труда. Каждая модель “Фиаско” требует затрат в размере 500 долл. на сырье и комплектующие изделия, тогда как каждая модель “каприз” требует затрат в размере 1500 долл.; суммарные затраты не должны превосходить 900 000 долл. в неделю. Рабочие, осуществляющие доставку, работают по 5 дней в неделю и могут забрать с завода не более 210 машин в день.

Каждая модель “Каприз” приносит фирме 1000 долл. прибыли, а каждая модель “Фиаско”- 500 долл. прибыли. Какой объем выпуска каждой модели вы бы порекомендовали? Что бы вы порекомендовали для повышения прибыли фирмы?

4.29. Заводы фирмы расположены в городах Лидсе и Кардиффе; они доставляют товары на склады городов Манчестер, Бирмингем и Лондон. Расстояния между этими городами приведены в таблице (расстояния округлены до десятков миль):

	Манчестер	Бирмингем	Лондон
Лидс
Кардифф

а) Завод в г. Лидсе выпускает в год 800 т. товаров, а в г. Кардиффе- 500 т. Манчестерский склад вмещает 400 т., бирмингемский- 600 т., а лондонский- 300 т. Как следует транспортировать товары для минимизации цен на перевозки?

б) На дороге Лондон- Кардифф ведутся работы, удваивающие стоимость перевозок по ней. Как бы вы пересмотрели расписание?

4.30. Фирма производит три вида продукции (А, В, С), для выпуска каждого из которых требуется определенное время обработки на всех четырех устройствах I, II, III, IV.

Вид	Время обработки, ч.	Прибыль,
продукции	I	II	III	IV	Долл.
А
В
С

Пусть время работы на устройствах- соответственно 84, 42, 21 и 42 ч. Определите, какую продукцию и в каких количествах следует производить. (Можете предположить, что рынок сбыта для каждого продукта неограничен; временем, требуемым для переключения устройства в зависимости от вида продукции, можно пренебречь; рассмотрите только задачу максимизации прибыли.)

4.31. Производитель безалкогольных напитков располагает двумя разливочными машинами А и В. Машина А спроектирована для пол-литровых бутылок, а машина В- для литровых, но каждая из них может использоваться для обоих типов бутылок с некоторой потерей эффективности в соответствии с приведенными в таблице сведениями о работе машин.

 

Машина	Количество бутылок, производимых в 1 мин.
	Пол-литровые бутылки	Литровые бутылки
А
В

Каждая из машин работает ежедневно по 6 ч. при пятидневной рабочей неделе. Прибыль от пол-литровой бутылки составляет 4 цента, а от литровой- 10 центов. Недельная продукция не может превосходить 50000 л.; рынок принимает не более 44000 пол-литровым бутылок и 30000 литровых.

Производитель хочет максимизировать свою прибыль при имеющихся средствах. Сформулируйте задачу в виде задачи линейного программирования и найдите оптимальное решение.

4.32. Производитель элементов центрального отопления изготовляет радиаторы четырех моделей. Ограничения на производство обусловленных количеством рабочей силы и количеством стальных листов, из которых изготовляются радиаторы.

Модель радиатора	А	В	С	D
Необходимое количество рабочей силы, человеко-часы	0,5	1,5		1,5
Необходимое количество стального листа, м^2.
Прибыль от продажи одного радиатора, долл.			12,5

В каких объемах выпускать продукцию, чтобы прибыль от продажи была максимальной?

4.33. Небольшая фирма производит два типа подшипников А и В, каждый из которых должен быть обработан на трех станках, а именно на токарном, шлифовальном и сверлильном. Время, требуемое для каждой из стадий производственного процесса, приведено в таблице.

Тип	Время обработки, ч.
подшипника	Токарный станок	Шлифоваль-ный станок	Сверлильный станок	Прибыль от продажи одного подшипника, центы
А	0,01	0,02	0,04
Б	0,02	0,01	0,01
полное возможное время работы в неделю, ч.

Фирма хотела бы производить подшипники в количествах, максимизирующих ее прибыль. Сформулируйте задачу как задачу линейного программирования и решите ее.

4.34. Фирма занимается составлением диеты, содержащей по крайней мере 20 единиц белков, 30 единиц углеводов, 10 единиц жиров и 40 единиц витаминов. Как дешевле всего достичь этого при указанных в таблице ценах на 1 кг. (или 1 л.) пяти имеющихся продуктов?

 

 

	Хлеб	Соя	Сушеная рыба	Фрукты	Молоко
Белки
Углеводы
Жиры
Витамины
Цена