Рациональное использование технологических участков

2.5.

Предприятию требуется за 30 дней выпустить 400 единиц Продукта1, 350 единиц Продукта2 и 800 единиц Продукта3. Продукция производится на трех различных технологических участках. Производительность каждого участка по каждому продукту (количество единиц продукции j-го вида j= , которое можно произвести на i-м участке i= в день) приведена в таблице.

Известны затраты на производство j-го продукта на i-м участке в день (см. табл.).

Требуется составить оптимальный план работы участков, т.е. найти сколько времени i-й участок будет занят производством j-го продукта с тем, чтобы общие издержки были наименьшими.

 

№ Участка	Производительность участков (ед-ц в день)
	Продукт1	Продукт2	Продукт3
План. объем вып-ка

Затраты на производство продукции (руб. в день)

№ Участка	Продукт1	Продукт2	Продукт3

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

230× x₁₁+190× x₁₂+140× x₁₃+230× x₂₁+180× x₂₂+130× x₂₃+190× x₃₁+140× x₃₂+100× x_33® min,

Ограничения имеют вид:

x₁₁+x₁₂+x_13£ 30,

x₂₁+x₂₂+x_23£ 30,

x₃₁+x₃₂+x_33£ 30,

20× x₁₁+14× x₂₁+12× x₃₁=400,

20× x₁₂+15× x₂₂+11× x₃₂=350,

15× x₁₃+20× x₂₃+15× x₃₃=800,

x_ij³ 0, i, j= .

Вид электронной таблицы Excel, созданной для решения задачи, представлен на рис. 28. Значения переменных x_ij располагаются в блоке ячеек B3:D5 (см. рис. 28). Коэффициенты целевой функции, отражающие затраты на производство продукции в единицу времени находятся по адресам B15:D17. Данные о производительности участков находятся в блоке B10:D12. Требования к планируемому объему выпуска каждого продукта заданы в ячейках B6:D6. Заданное время работы участков введено в E10.

Рис. 28

Рис. 29

Формулы целевой функции и ограничений находятся соответственно в ячейке E7 и ячейках B7:D7 (ограничения по плану), E3:E5 (ограничения по времени) (см. рис. 28 и 29). Вид электронной таблицы в режиме отображения формул представлен на рис. 29.

Запись условий задачи в окне "Поиск решения" можно увидеть на рис. 30.

Результаты поиска решения приведены на рис. 28.

Рис. 30

 

Закрепление самолетов за воздушными линиями

Три типа самолетов требуется распределить между четырьмя авиалиниями. В приводимых ниже таблицах задано число самолетов каждого типа, месячный объем перевозок каждым самолетом на каждой авиалинии и соответствующие эксплуатационные расходы.

Требуется распределить самолеты по авиалиниям так, чтобы при минимальных суммарных эксплуатационных расходах перевезти по каждой из четырех авиалиний соответственно не менее 300, 200, 1000 и 500 единиц груза.

 

Тип самолета	Число самолетов	Месячный объем перевозок одним самолетом по авиалиниям
		I	II	III	IV

 

Тип самолета	Эксплуатационные расходы
	I	II	III	IV

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

15× x₁₁+20× x₁₂+25× x₁₃+40× x₁₄+70× x₂₁+28× x₂₂+15× x₂₃+45× x₂₄+40× x₃₁+70× x₃₂+40× x₃₃+65× x_34® min,

Ограничения имеют вид:

15× x₁₁+30× x₂₁+25× x_31³ 300,

10× x₁₂+25× x₂₂+50× x_32³ 200,

20× x₁₃+10× x₂₃+30× x_33³ 1000,

50× x₁₄+17× x₂₄+45× x_34³ 500,

x₁₁+x₁₂+x₁₃+x₁₄=50,

x₂₁+x₂₂+x₂₃+x₂₄=20,

x₃₁+x₃₂+x₃₃+x₃₃=30,

x_ij³ 0, целые (i= , j= ).

Вид электронной таблицы Excel, созданной для решения задачи, представлен на рис. 31. Значения переменных x_ij располагаются в блоке ячеек B4:E6 (см. рис. 31). Коэффициенты целевой функции, отражающие расходы на перевозку находятся по адресам B18:E20. Данные о месячных объемах перевозок одним самолетом имеются в блоке B12:E14. Задан план перевозок и число самолетов- соответственно блоки B7:E7 и F4:F6.

Рис. 31

Формулы целевой функции и ограничений находятся соответственно в ячейке F8 и ячейках B8:E8 (ограничения по плану), F4:F6 (ограничения по количеству самолетов) (см. рис. 31 и 32). Вид электронной таблицы в режиме отображения формул представлен на рис. 32.

Рис. 32

Рис. 33

В группе Ограничения (см. рис. 33) заданы, помимо остальных, ограничения на целочисленность переменных (первая запись), означающие, что количество выбранных самолетов (значения x_ij) должно быть целым числом. Задание ограничения на целочисленность увеличивает время вычислений Поиска решения.

Результаты поиска решения приведены на рис. 31.

 

Задача о ранце

 

В грузовую автомашину надо поместить четыре вида предметов, причем могут потребоваться несколько одинаковых предметов. Имеется три вида ограничений такого типа, как вес, объем и т.д. В приведенной ниже таблице даны a_ij- i-я характеристика предмета j-го наименования, c_j- полезность одного предмета j-го наименования (i= , j= ). Требуется загрузить машину так, чтобы суммарная полезность груза была максимальной.

Ограничения	Предмет1	Предмет2	Предмет3	Предмет4	Значения ограничений
I
II
III
Полезность

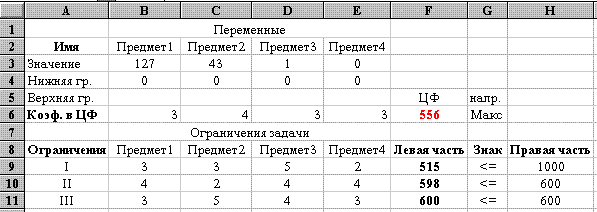
Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

3× x₁+4× x₂+3× x₃+3× x_4® max,

Ограничения имеют вид:

3× x₁+3× x₂+5× x₃+2× x_4£ 1000,

4× x₁+2× x₂+4× x₃+4× x_4£ 600,

3× x₁+5× x₂+4× x₃+3× x_4£ 600,

x_j³ 0, целые, j= .

Вид электронной таблицы Excel, созданной для решения задачи, представлен на рис. 34. Значения переменных x_ij располагаются в блоке ячеек B3:E3 (см. рис. 34). Коэффициенты целевой функции, отражающие полезности предметов находятся по адресам B6:E6. Данные о характеристиках предметов имеются в блоке B9:E11. Заданы значения ограничений- соответственно блок H9:H11.

Рис. 34

Формулы целевой функции и ограничений находятся соответственно в ячейке F6 и ячейках F9:E11 (ограничения по свойствам) (см. рис. 34 и 35). Вид электронной таблицы в режиме отображения формул представлен на рис. 35.

Запись условий задачи в окне "Поиск решения" можно увидеть на рис. 36.

Результаты поиска решения приведены на рис. 34.

Рис. 35

Рис. 36