
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель рационального использования посевных площадейСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Имеется m земных угодий S1,...,Sm, предназначенных для засева той или иной сельскохозяйственной культурой. Эти площади отличаются либо положением, либо характером почвы. На каждом из угодий (полей) Si, i=1,...,m, могут быть размещены одна или несколько из n сельскохозяйственных культур Q1,...,Qn (пшеница, рожь, кукуруза, картофель и т. д.). Пусть известна урожайность культуры Qj на поле Si; она равна aij центнеров с гектара. Будем обозначать площадь поля Si в гектарах через ai. Ограничения в этой задаче таковы: задан план производства bj каждой сельскохозяйственной культуры Qj. Известны закупочные цены cj на каждый вид Qj продукции. Требуется определить план засева посевных площадей с целью максимизации дохода от продажи сельскохозяйственной продукции. Пусть xij- площадь (в гектарах) на i-м поле, занятая культурой Qj. Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарную прибыль от реализации выращенной продукции. Ограничения имеют вид:
xij³ 0, i= Условия (1) означают, что сумма площадей i-го поля, занятых под j-е культуры равна площади i-го поля. Условия (2) представляют ограничения по минимальному объему выращиваемой продукции.
Модель рационального использования имеющихся мощностей
Пусть предприятию задан план производства по времени и номенклатуре: требуется за время Т выпустить b1, b2,..., bn единиц продукции вида 1, 2,..., n, продукция производится на N различных технологических участках. Производительность каждого из участков задана коэффициентом аij, который показывает, сколько единиц продукции j-го вида ( Известны издержки cij, отражающие все затраты на изготовление продукции j-го вида на i-м участке в единицу времени. Требуется составить оптимальный план работы участков, а именно: найти, сколько времени i-й участок будет занят изготовлением j-й продукции с тем, чтобы общие издержки были наименьшими. Сведем данные в таблицу.
Обозначим переменные модели через xij, которые означают время работы i-го участка при изготовлении j-й продукции.
Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарные затраты на производство продукции. Ограничения имеют вид:
xij³ 0, i= Условия (1) предполагают, что время работы каждого станка ограничено и не превышает числа Т. Условия (2) обеспечивают выполнения плана по номенклатуре.
Задача о закреплении самолетов за воздушными линиями
Эта задача возникает при выборе оптимального варианта плана закрепления самолетов за данными воздушными линиями, обеспечивающего необходимые объемы перевозок при минимальных суммарных эксплуатационных расходах. Пусть имеется n различных типов самолетов, которые нужно распределить между m авиалиниями. Пусть месячный объем перевозок самолетом i-го типа на j-й авиалинии равен аij единицам, а связанные с этим месячные эксплуатационные расходы составляют cij рублей. Определить число xij самолетов i-го типа, которое следует закрепить за j-й авиалинией для обеспечения перевозки по этой линии аij единиц (i= Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарные эксплуатационные расходы в месяц. Ограничения имеют вид:
xij³ 0, xij- целые числа, i= Условия (1) определяют, что самолеты j-й авиалинии должны обеспечивать объем перевозок не меньше заданного. Условия (2) представляют собой ограничение по количеству имеющихся самолетов i-го типа. Данная задача является задачей целочисленного линейного программирования.
Задача о ранце
Здесь речь идет о собравшемся в поход путешественнике, который должен упаковать в ранец различные полезные предметы n наименований, причем могут потребоваться несколько одинаковых предметов. Имеются m ограничений такого типа, как вес, объем, линейные размеры и т.д. Пусть аij- i-я характеристика предмета j-го наименования i=
Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарная полезность собранных предметов. Ограничения имеют вид:
xj³ 0, xj- целое, j= Условия (1) означают, что количество отобранных предметов не превышает возможностей погрузки. Данная задача является задачей линейного целочисленного программирования.
Задача о назначениях
Имеется n работников, которых требуется назначить на n работ. Известно, что j-ю работу i-й работник будет выполнять с эффективностью cij. Требуется так распределить работников, чтобы максимизировать суммарную эффективность. Положим xij=1, если i-й работник назначен на j-ю работу; xij=0, в противном случае, i, j= Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарную эффективность. Ограничения имеют вид:
xij равно либо 0, либо 1. Условия (1) означают, что каждый работник назначается только на одну работу. Условия (2) означают, что один работник выполняет только одну работу. Данная задача является задачей линейного булева программирования.
Задача коммивояжера
Имеется n городов. Выезжая из исходного города А1, коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город А1. Задача заключается в определении последовательности объезда городов при которой коммивояжеру требуется минимизировать некоторый критерий эффективности: стоимость проезда, время в пути, суммарное расстояние и т.д. Пусть задана матрица C=||cij|| расстояний между городами и требуется минимизировать суммарную длину пути. Введем переменные xij=1, если коммивояжер переезжает из города Аi в город Аj, i¹ j; xij=0, в противном случае, i, j= Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарную длину пути. Ограничения имеют вид:
ui-uj+(n-1)× xij £ n-2, 2£ i¹ j £ n, (3) где ui, i= Условия (1) означает, что коммивояжер выезжает из каждого города один раз, а условия (2)- что он въезжает один раз в каждый город. Условия (3), выглядящие несколько искусственно, предназначены обеспечить связность маршрута коммивояжера. Более точно эти условия запрещают любой цикл, не проходящий через город 1, и тем самым исключают ситуации, подобные приведенной на рисунке.
1 2 5 6
Данная задача является задачей линейного булева программирования.
1.10. Задача о доставке (покрытии множества)
Фирма обслуживает некоторое количество клиентов (m). Каждый день она доставляет своим клиентам товары на грузовых машинах (или по железной дороге, воздушным путем, на баржах и т.д.). Существует множество допустимых маршрутов (n) доставки, каждый из которых позволяет обслужить определенное подмножество клиентов и требует использования в течении дня одного транспортного средства. Каждый маршрут характеризуется определенными расходами, которые могут соответствовать его длине, или стоимости расходуемого топлива и т.д. Цель состоит в том, чтобы выбрать такое множество маршрутов, при котором обеспечивается обслуживание каждого из клиентов, каждый клиент обслуживается один раз в день и суммарные расходы минимальны.
Введем переменные: xj=1, если маршрут j выбран; xj=0, в противном случае, j= Обозначим элементы aij следующим образом: aij=1, если i-й клиент обслуживается по маршруту j; aij=0, в противном случае, i= Обозначим стоимость доставки по маршруту j через сj. Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарные расходы доставки по выбранным маршрутам. Ограничения имеют вид:
Согласно условиям (1) каждый клиент обслуживается один раз в день. Данная задача является задачей линейного булева программирования.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 502; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.97.150 (0.009 с.) |

 ® max.
® max. , i=
, i=  , (1)
, (1) , j=
, j=  , (2)
, (2)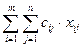 ® min.
® min. ® min.
® min. ³ aj, j=
³ aj, j=  =Ni, i=
=Ni, i=  ® max.
® max. i=
i=  ® max.
® max. , j=
, j= 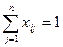 , i=
, i=  ® min.
® min. , j=
, j=  - неограниченные действительные переменные.
- неограниченные действительные переменные. 4 3 7
4 3 7


 ® min.
® min. =1, i=
=1, i= 


