
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий разрешимости задачи ЛПСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Следствие 1 (Теорема существования) Для того, чтобы в двойственных задачах 1 и 1* существовали оптимальные векторы х и у, т.е. имел место случай 1 теоремы двойственности, достаточно выполнения одного из следующих условий: 1. в задаче 1 существует оптимальный вектор х 2. в задаче 1* существует оптимальный вектор у 3. в задаче 1 существует допустимый вектор х и функция 4. в задаче 1* существует допустимый вектор у и функция 5. в задачах 1 и 1* существуют допустимые векторы х и у
Следствие 2 (Необходимый признак оптимальности) Допустимый признак оптимальности в краткой и развернутых формах является так же необходимым признаком. Доказательство: пусть имеется оптимальный вектор х в задаче 1 и оптимальный вектор у в задаче 1*. Тогда на основании условий 2 теоремы о существовании имеет место случай 1 теоремы двойственности, то есть Экономическая интерпретация двойственных задач
Экономическая интерпретация двойственных задач
Прямые задачи линейного программирования в канонической форме
Двойственные задачи линейного программирования в канонической форме
Признак оптимальности для задач ЛП в канонической форме
Замечание. Наиболее удобной для решения задач ЛП является 2 каноническая форма Вторая каноническая форма задачи ЛП в векторной форме Введем в рассмотрение m -мерные векторы: Тогда задачи 3 и 3* запишутся в следующей форме:
Базисное множество
Пусть Множество К называют базисным множеством, если отвечающие ему векторы
на множестве n -мерных векторов х = (х1, х2,..., хn), удовлетворяющих условиям 1. 2. Пример. Векторы
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 518; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

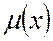 ограничена сверху
ограничена сверху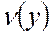 ограничена снизу
ограничена снизу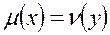 .
.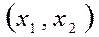 продукции I и II-го видов, обеспечивающий наибольшую прибыль (задача ЛП).
продукции I и II-го видов, обеспечивающий наибольшую прибыль (задача ЛП).
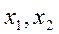 :
:
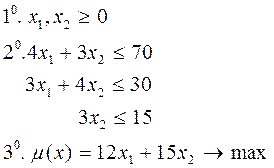
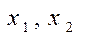 :
:
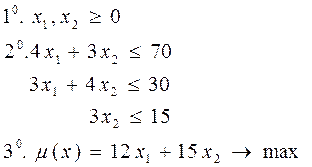 Это же предприятие получило возможность продавать отходы производства, для чего ему необходимо определить их цену. Пусть
Это же предприятие получило возможность продавать отходы производства, для чего ему необходимо определить их цену. Пусть 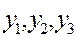 - цена единицы отходов 1,2,3 - го видов. Естественно, что покупатель стремится к тому, чтобы суммарная цена всех отходов была наименьшей, а предприятию выгодно продавать их лишь в том случае, если выручка от продажи не меньше, чем прибыль от реализации готовых изделий.
- цена единицы отходов 1,2,3 - го видов. Естественно, что покупатель стремится к тому, чтобы суммарная цена всех отходов была наименьшей, а предприятию выгодно продавать их лишь в том случае, если выручка от продажи не меньше, чем прибыль от реализации готовых изделий.
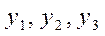 :
:
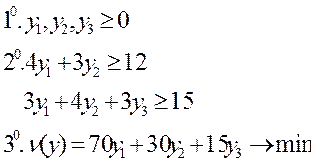 Задачи I и II являются парой двойственных задач.
Задачи I и II являются парой двойственных задач.
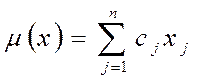 на множестве векторов х= (х1,х2, …хn,),
удовлетворяющих условиям:
1. хj ³0 для jÎJ2
2.
на множестве векторов х= (х1,х2, …хn,),
удовлетворяющих условиям:
1. хj ³0 для jÎJ2
2. 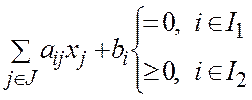
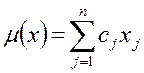 на множестве векторов
на множестве векторов 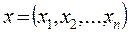 удовлетворяющих условиям
1.
удовлетворяющих условиям
1. 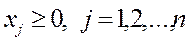 2.
2. 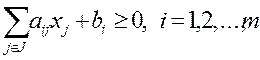 I2=I ={1,2,…, m }
J2 J2 =J ={1,2,…, n }
I2=I ={1,2,…, m }
J2 J2 =J ={1,2,…, n }
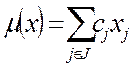 на множестве векторов
на множестве векторов 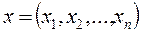 удовлетворяющих условиям:
1.
удовлетворяющих условиям:
1. 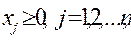 2.
2. 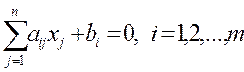 I1=I ={1,2,…, m }
J2 J2 =J ={1,2,…, n }
I1=I ={1,2,…, m }
J2 J2 =J ={1,2,…, n }
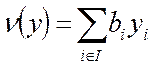 на множестве векторов y= (y1,y2,…..ym),
удовлетворяющих условиям:
1. yi ≥ 0 для iÎI2
2.
на множестве векторов y= (y1,y2,…..ym),
удовлетворяющих условиям:
1. yi ≥ 0 для iÎI2
2.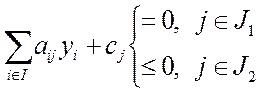
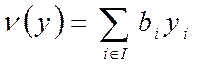 на множестве векторов
на множестве векторов 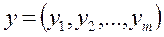 , удовлетворяет условиям 1.
, удовлетворяет условиям 1. 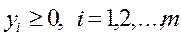 2.
2. 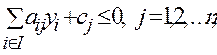
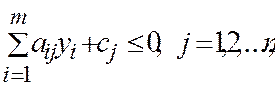
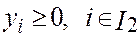 б)
б) 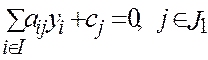 в)
в) 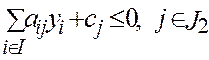 г)
г) 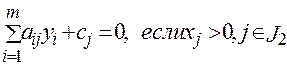 д)
д) 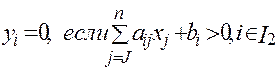
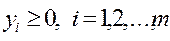 б) –
в)
б) –
в) 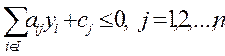
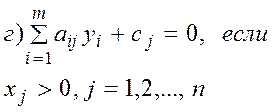
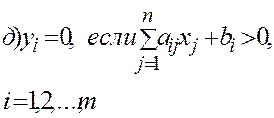
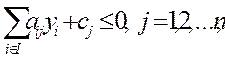
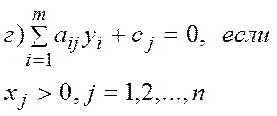 д) –
д) –
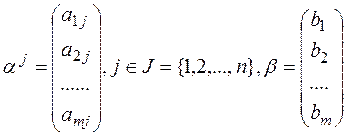
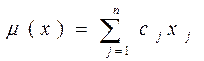 на множестве n -мерных векторов
х = (х1, х2,..., хn),
удовлетворяющих условиям
1.
на множестве n -мерных векторов
х = (х1, х2,..., хn),
удовлетворяющих условиям
1. 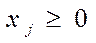 ,
, 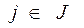 ,
2.
,
2. 
 на множестве m-мерных векторов
y = (y1, y2,..., ym),
удовлетворяющих системе линейных неравенств
1. -
2.
на множестве m-мерных векторов
y = (y1, y2,..., ym),
удовлетворяющих системе линейных неравенств
1. -
2. 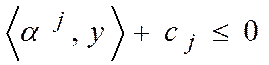 ,
,  .
.
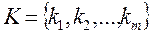 – m -мерное подмножество множества J.
– m -мерное подмножество множества J.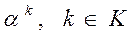 являются линейно независимыми, т.е. образуют базис в пространстве Rm. Число векторов в базисном множестве К равно числу m уравнений в условии 2 задачи А:
являются линейно независимыми, т.е. образуют базис в пространстве Rm. Число векторов в базисном множестве К равно числу m уравнений в условии 2 задачи А: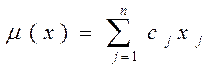 → max
→ max - линейно независимые, т.к.
- линейно независимые, т.к.  , К= { 1,2 }.
, К= { 1,2 }.


