
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая интерпретация задач линейного программированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
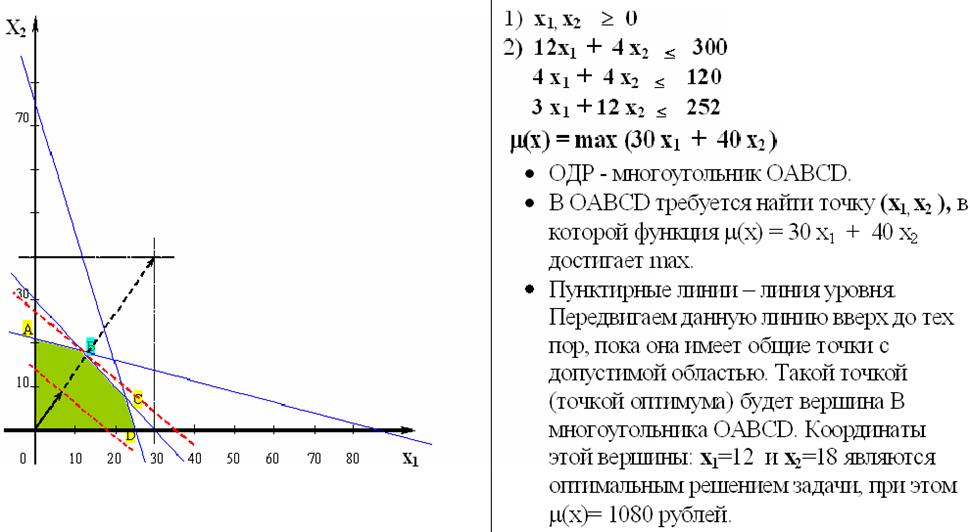
Геометрическая интерпретация задач линейного программирования
Графический метод решения задач ЛП При нахождении решения задачи ЛП графическим методом могут встретиться следующие случаи:
Целевая функция m принимает Целевая функция m принимает max в любой max в единственной точке А точке отрезка АВ
Графический метод решения задач ЛП При нахождении решения задачи ЛП графическим методом могут встретиться следующие случаи:
Целевая функция не ограничена сверху Система ограничений задачи несовместна на множестве допустимых решений (некорректная постановка задачи). Нет ОДР
Общая форма задачи ЛП Пусть заданы: множества I ={1,2…m} и J= {1,2…n}, причем I= I1U I2, I1 Ç I2 = Æ, J= J1UJ2, J1Ç J2 = Æ, вещественные числа аij, iÎI, jÎJ; bi, iÎI, сj, jÎJ.
ЗАДАЧА 1 (прямая со смешанными ограничениями) Максимизировать линейную функцию
на множестве векторов х= (х1,х2, …хn,), (2) удовлетворяющих условиям:
1. хj ³0 для jÎJ2 (3) 2.
Двойственная задача ЛП ЗАДАЧА 1* (двойственная со смешанными ограничениями). Минимизировать линейную функцию
на множестве векторов y= (y1,y2,…..ym), (6) удовлетворяющих условиям: 1. yi ≥ 0 для iÎI2 (7) 2.
Определение. Векторы (2), (6), удовлетворяющие условиям (3), (4) и (7), (8) называются допустимым для задачи 1 и задачи 1* соответственно. Допустимые векторы (2), (6), доставляющие максимум функции (1) и минимум функции (5) соответственно, называются оптимальными. Правила составления двойственной задачи ЛП
В задаче 1 имеется n-переменных и m- ограничений типа (4). В задаче 1* имеется m –переменных и n-ограничений типа (8). Это значит, что каждой переменной в задаче 1 соответствует ограничение в задаче 1* и каждому ограничению в задаче 1 соответствует переменная в задаче 1*. В задаче 1 требуется максимизировать целевую функцию на множестве заданных ограничений больше 0. В задаче 1* требуется минимизировать целевую функцию на множестве заданных ограничений меньше 0. Коэффициенты сj линейной функции (1) в задаче 1 являются свободными членами ограничений (8) задачи 1*, свободные члены bi ограничений (4) в задаче 1 являются коэффициентами линейной функции (5) задачи 1*. Коэффициенты при неизвестных аij в задачах 1 и 1* одни и те же, но матрицы из этих коэффициентов транспонированы по отношению друг к другу. В задаче 1 все неравенства типа ³, а в задаче 1* все неравенства типа £. Если на переменную задачи 1 налагается условие неотрицательности, то соответствующее ограничение в двойственной задаче является неравенством, а если условия неотрицательности на переменную нет, то соответствующее ограничение в задаче 1* является уравнением. И наоборот.
Пример составления двойственной задачи ЛП
Пример составления двойственной задачи ЛП
Связь между задачами 1 и 1*
Связь между парой двойственных задач устанавливает следующая лемма 1: Для любых допустимых векторов х и у в задачах 1 и 1* выполняются неравенства µ(x) £ причем (9) выполняется как равенство в том и только в том случае, если справедливы следующие соотношения:
Связь между задачами 1 и 1* Доказательство. Имеем:
Связь между задачами 1 и 1* Доказательство (продолжение). Имеем:
yi ≥ 0 для iÎI2
Правые части в соотношениях (13) и (15) отличаются лишь порядком суммирования и, следовательно, равны между собой, т.е. выполняется µ(x) £
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.162.166 (0.009 с.) |



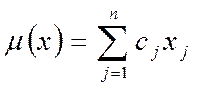 (1)
(1)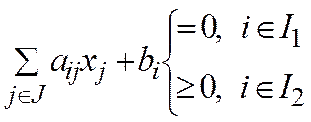 (4)
(4)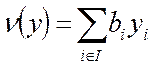 (5)
(5)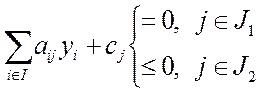 (8)
(8)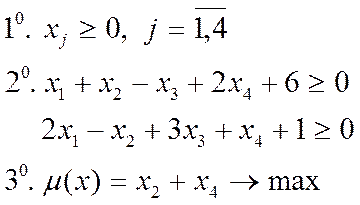
 т.е все переменные связаны условием неотрицательности, и все ограничения выполняются как неравенства. Двойственная задача имеет вид:
ЗАДАЧА 1*
Найти
т.е все переменные связаны условием неотрицательности, и все ограничения выполняются как неравенства. Двойственная задача имеет вид:
ЗАДАЧА 1*
Найти 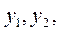 удовлетворяющие условиям:
удовлетворяющие условиям:
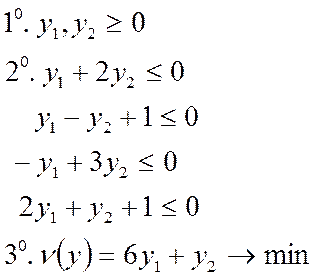
 =2x1 — х2 + Зх3 + х4 — 5x5
на множестве пятимерных векторов
х = (х1, х2, х3, х4, х5),
удовлетворяющих условиям
=2x1 — х2 + Зх3 + х4 — 5x5
на множестве пятимерных векторов
х = (х1, х2, х3, х4, х5),
удовлетворяющих условиям
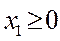 ,
,  ,
, 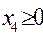 ,
Зх1 + 2х2 - 5х3 + х5 - 7
,
Зх1 + 2х2 - 5х3 + х5 - 7  0,
3х2 - 4х3 - 2х4 + 1 = 0,
2х1 + 2х3 - 3х4 + х5
0,
3х2 - 4х3 - 2х4 + 1 = 0,
2х1 + 2х3 - 3х4 + х5 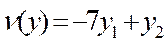 на множестве трехмерных векторов, удовлетворяющих условиям
на множестве трехмерных векторов, удовлетворяющих условиям
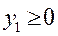 ,
, 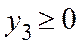 ,
3y1 + 2y3 + 2
,
3y1 + 2y3 + 2  0,
2y1 + 3y2 -1 = 0,
- 5y1 + 4y2 + 3y3 + 3
0,
2y1 + 3y2 -1 = 0,
- 5y1 + 4y2 + 3y3 + 3  (у), (9)
(у), (9) (10)
(10)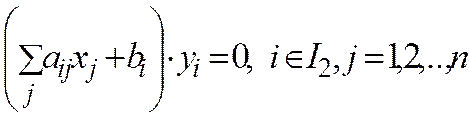 (11)
(11)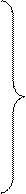 хj ³0 для jÎJ2
хj ³0 для jÎJ2
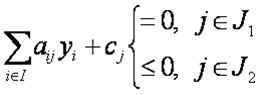
 (12)
(12) Суммируя полученные соотношения, получим с учетом того, что
Суммируя полученные соотношения, получим с учетом того, что  (13)
(13)

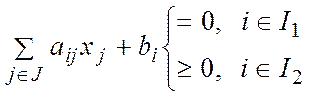

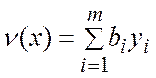
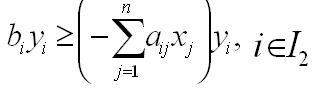 (14)
(14)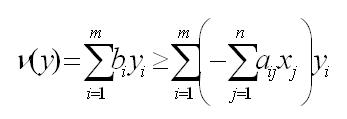 (15)
(15)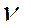 (у) (9). Для достижения равенства в (9), очевидно, необходимо и достаточно, чтобы достигались равенства во всех неравенствах (13) и (15). Последнее эквивалентно выполнению соотношений (10) и (11) ▄
(у) (9). Для достижения равенства в (9), очевидно, необходимо и достаточно, чтобы достигались равенства во всех неравенствах (13) и (15). Последнее эквивалентно выполнению соотношений (10) и (11) ▄


