Несбалансированность в транспортной задаче

Если сумма запасов превышает сумму заказов (излишек запасов) или, наоборот сумма запасов меньше, чем сумма заказов (дефицит запасов) необходимо сбалансировать задачу. В первом случае,

нужно добавить в таблицу транспортных издержек и в таблицу перевозок по одному лишнему столбцу.

Это можно трактовать так, как если бы появился еще один «фиктивный» потребитель. Если потребовать, чтобы заказ этого «потребителя» в точности равнялся бы разности между суммой всех запасов и суммой всех заказов

а издержки перевозок грузов к нему от любого поставщика равны нулю, будем иметь сбалансированную транспортную задачу. При этом переменные решения в последнем столбце дадут количество грузов, которые должны остаться на каждом из складов.

Во втором случае, когда

нужно добавить в таблицу транспортных издержек и в таблицу перевозок по одной лишней строчке. Это можно трактовать так, как если бы появился еще один «фиктивный» поставщик. Потребуем, чтобы запас этого «поставщика» в точности равнялся бы разности между суммой всех заказов и суммой всех запасов

а издержки перевозок грузов от него к любому поставщику равны нулю. Вновь имеем сбалансированную транспортную задачу. При этом переменные решения в лишней строчке – это тот объем грузов, которые не получит каждый потребитель.

Заметим, что несбалансированные транспортные задачи можно, конечно, решать и просто заменив в соответствующих ограничениях знаки равенств на знаки нестрогих неравенств. Однако при этом надо иметь в виду, что для решения такой задачи MS-Excel будет применять общие методы решения ЛП- задач, а не специфические «транспортные» алгоритмы. В результате эффективность решения может быть значительно ниже, и получение целочисленного решения не гарантируется.

Еще одно возможное осложнение транспортной задачи – это запрещение определенной перевозки от i-го поставщика к j-му потребителю для составляемого плана перевозок (ремонт дороги, неплатеж и пр.). В этом случае, естественно, можно просто ввести ограничение x_ij =0. Однако, это вновь означает невозможность использования эффективных «транспортных» алгоритмов решения.

Чтобы сохранить форму транспортной задачи и учесть этот запрет, достаточно в таблице транспортных издержек заменить c_ij на очень большое число (на порядок большее, чем максимальная цена перевозки в таблице транспортных издержек). Это фактически будет означать, что оптимизационный алгоритм наверняка положит соответствующее значение перевозки x_ij равным нулю, поскольку перевозка по этому маршруту просто крайне невыгодна.

Подробнее о постановке и методах решения транспортной задачи можно узнать в [1, 3, 4].

 

Примеры решения задач

Пример 2.1 Дорстрой

С шести асфальтобетонных заводов должен вывозиться асфальт для строительства 5 участков автодорог области. Транспортные издержки при перевозках, разумеется, в общем случае различны (см. таблицу).

Транспортные издержки:

	Участок A	Участок B	Участок C	Участок D	Участок E
АБЗ 16
АБЗ 17
АБЗ 18
АБЗ 19
АБЗ 20
АБЗ 21

Заказы дорожно-строительных бригад на завтра:

Потребитель	Участок A	Участок B	Участок C	Участок D	Участок E
Количество машин

 

Заводы в состоянии предоставить завтра:

Источник	АБЗ 16	АБЗ 17	АБЗ 18	АБЗ 19	АБЗ 20	АБЗ 21
Кол-во машин

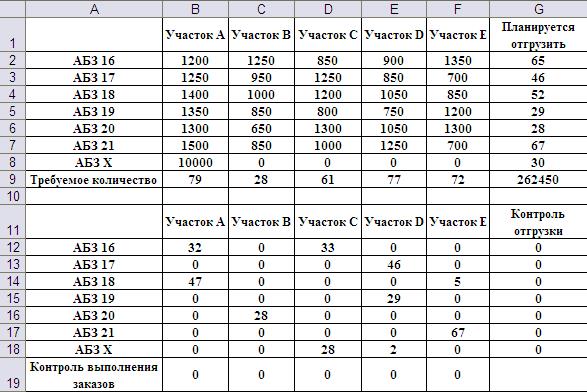
чего, очевидно, недостаточно, т.к. заказов 79+28+61+77+72=317, а поставок 65+46+52+29+28+67=287

Менеджер подрядной организации хочет минимизировать транспортные расходы для данных условий.

1. Каковы наименьшие транспортные издержки?

2. Сколько машин, и на какие участки будет недопоставлено?

3. После составления плана менеджер получил указание, по причинам неэкономического характера, план поставок асфальта для участка А необходимо выполнить полностью. Каковы транспортные издержки нового плана? Сколько машин, и на какие участки будет недопоставлено в этом случае?

4. При утверждении нового плана у руководства, выяснилось, что из-за аварийного состояния моста перевозка асфальта с АБЗ 21 на участок Е по прямому маршруту невозможна. Объездной маршрут увеличивает стоимость рейса на 300 рублей. Насколько при этом возрастут транспортные расходы? Что выгоднее, оставить почти утвержденный план, несмотря на увеличении издержек, или составить новый план с учетом сложившейся ситуации?

5. Есть ли у задачи альтернативные решения?

#

Решение задачи.

Данную транспортную задачу следует трактовать как простую. Правда, дополнительные вопросы могут оказаться не такими уж простыми, но, в любом случае, задачу следует сначала решить в основной постановке.

Как обычно, сначала проверяем, сбалансирована ли задача, так как дисбаланс сразу нужно будет учесть при правильной организации данных на листе Excel. Общее количество машин асфальта, которые можно вывезти с заводов – 287 штук. Общий заказ дорожно-строительных бригад – 317 машин.

Действительно, как и сказано в тексте задачи имеется дисбаланс заказов и запасов. Размер дисбаланса – 317-287=30 машин.

Для того чтобы сбалансировать задачу нужно добавить недостающего поставщика асфальта мощностью в 30 машин в день. Это учтено при построении таблицы (Рис.1).

Рис.1. Организация рабочего листа для решения транспортной задачи примера 2.1

 

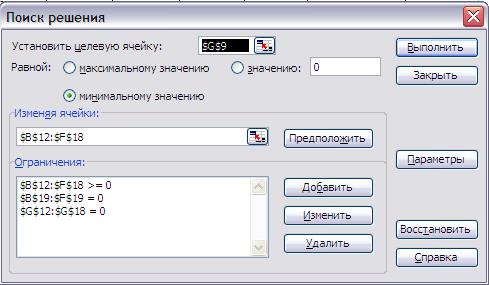
Фиктивному поставщику асфальта присвоено имя АБЗ X. Перевозки от фиктивного поставщика считаются бесплатными. Так как стоимость перевозок от отдельных поставщиков нас не интересует, мы рассчитываем сразу суммарную стоимость перевозок, перемножая таблицу цен B2:F8 на таблицу перевозок B12:F18 с помощью функции =СУММПРОИЗВ(). Суммарная стоимость всех перевозок и есть целевая функция задачи (ячейка G9).

Стандартные условия транспортной задачи - должно быть доставлено ровно столько, сколько заказано, и должно быть вывезено все, что предложено – могут быть заданы с помощью записанных в строке B19:F19 и столбце G12:G18 выражений.

Вызываем надстройку Поиск решения и ставим задачу. Целевая ячейка – G9, цель – минимум издержек. Изменяемые ячейки – таблица перевозок B12:F18.

Параметры решения – линейная модель и неотрицательные значения переменных. Ограничения - B19:F19=0 и G12:G18=0 (Рис.2).

Рис.2. Установка опций Поиска решения при решении п.1 примера 2.1

Результаты решения представлены на Рис.3.

Рис.3. Результат решения задачи по пунктам 1 и 2 примера 2.1

План составлен, общие издержки – 251 950 руб. – минимальные из всех возможных при выполнении заказов бригад. Все недопоставленные машины пришлись на долю участка A(перевозки от поставщика АБЗ Х).

Если мы хотим угодить некоему, оставшемуся неназванным лицу, и выполнить заказ участка А полностью, нужно как-то изменить таблицу цен.

Дополнительные ограничения в задание для Поиска решения добавлять нежелательно. Более разумно задать цену перевозок от фиктивного поставщика. До сих пор мы не задавали в ценах перевозок от фиктивного поставщика разных цен. И делали это именно потому, что хотели поставить всех клиентов в равные условия, по отношению к такому фиктивному поставщику. А что, если условия не равные? В таком случае мы можем поставить в качестве цены перевозки от АБЗ Х на участок А какое-нибудь большое число, которое фактически запретит данную перевозку для Поиска решения.

Ставим цену 10 тыс. за машину и вновь ищем решение (Рис.4).

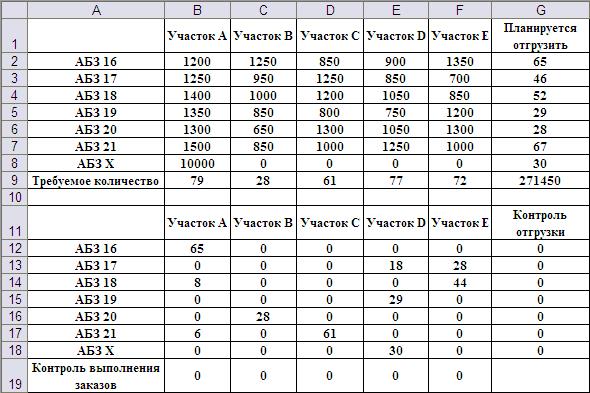
Рис.4. Результат решения задачи по пункту 3 примера 2.1 при задании цены от фиктивного перевозчика.

Теперь вся недопоставка пришлась на долю участков С и D. Общая цена вопроса 10,5 тыс. рублей (262450-251950) – именно на столько возросли издержки перевозок после волевого решения выполнить план поставок на участок А.

Для ответа на вопрос 4 сначала изменим цену перевозки от АБЗ 21 на участок Е на 300 рублей и позволим Excel пересчитать текущие издержки.

Рис.5. Результат решения задачи по пункту 4 примера 2.1 при задании цены от фиктивного перевозчика.

Получаем общие издержки в 271 450 рублей, что выше, чем в последнем плане перевозок на 9 000 руб.

Задачи для самостоятельного решения