Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение оптимального объёма заказаСодержание книги
Поиск на нашем сайте
В лабораторной работе рассматриваются стратегии принятия оптимальных решений в условиях риска для торговых предприятий. Одной из важных задач, решаемых предприятиями торговли, является определение оптимального объёма заказа на товары у поставщика. Недозаказ может привести к неудовлетворённому спросу и, следовательно, к недополучению прибыли. А заказ излишнего количества товара может привести к необходимости реализации перезаказанного товара по ценам ниже закупочных цен, что вызовет прямые убытки. Решающим фактором при определении объёма заказа является спрос, который подвержен влиянию множества случайных факторов: тенденциям моды, погоды и др. Задача принятия оптимального решения проводится на основе анализа матрицы полезности (или прибыли)
Строки матрицы соответствуют состояниям среды (спросу), а столбцы принимаемым решениям (объёмам заказа). Элемент матрицы Конкретизируем задачу для следующей ситуации. Менеджер небольшой кондитерской «Сластёна» решает вопрос, сколько пирожных следует иметь в запасе, чтобы удовлетворить спрос покупателей. Каждое пирожное обходится у поставщика в 10 руб., а кондитерская продаёт его по 15 руб. Продать невостребованные пирожные на следующий день невозможно, поэтому остаток распродаётся в конце дня по 5 руб. за штуку. Перечисленные цены сведены в таблицу
За сорок пять предыдущих дней работы была набрана статистика на спрос.
Сформируем матрицу полезности для данного случая. Количество проданных пирожных определяется выражением
где: Заполнение матрицы полезности по выведенной формуле приведет к результату.
На практике применяют два правила принятия оптимального решения: · правило максимальной вероятности; · правило максимальной средней прибыли. Правило максимальной вероятности – максимизация наиболее вероятных доходов. При этом в матрице доходов выбирают состояния спроса, имеющие наибольшие вероятности, и в пределах этих состояний выбирают решение, которое даёт наибольший доход. На Рис.1 показана подготовка листа приложения MS Excel для автоматизации данного правила. Адресация в формуле ячейки позволяет распространить её во все ячейки матрицы полезности. Поэтому ряд столбцов на Рис. 1 скрыт.
Рис.1. Ввод формул для реализации правила максимальной вероятности. Оптимальное решение по правилу максимальной вероятности для приведённых исходных данных соответствует объёму закупки 400 (Рис.2).
Рис.2. Оптимальное решение для правила максимальной вероятности. Правило средней прибыли. Этот способ использования вероятностных характеристик при принятии решения является наиболее распространённым. Решающее правило для определения оптимальной стратегии
где: Т.е., сначала получают средние значения прибылей в пределах каждого столбца, а затем из столбцов (объёмов закупок) выбирается тот, для которого среднее значение максимально. На Рис.3 и Рис.4, соответственно, показаны подготовка листа для автоматизации принятия решения и результат выбора по данному правилу. Оптимальный объём закупки в данном случае равен 300, что отличается от результата, полученного по правилу максимальной вероятности.
Рис.3. Ввод формул для реализации правила максимальной ожидаемой прибыли.
Рис.4. Оптимальное решение для правила максимальной ожидаемой прибыли.
В том случае если максимальных средних значений по столбцам окажется несколько, следует отдать предпочтение тому, для которого среднеквадратическое отклонение окажется меньшим. Задачи для самостоятельного решения
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.60.132 (0.005 с.) |

 [1, 3, 5]
[1, 3, 5]



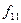




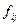







 . В самом деле, если
. В самом деле, если  , то реализуется
, то реализуется  , то реализуется
, то реализуется  пирожных. Это соотношение предполагает и нулевое значение, если
пирожных. Это соотношение предполагает и нулевое значение, если 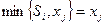 . Затраты на закупку составят
. Затраты на закупку составят  . Следовательно, элемент
. Следовательно, элемент 
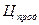 - цена продажи,
- цена продажи,  - цена распродажи.
- цена распродажи.


 формально записывается так
формально записывается так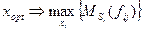 ,
, - математическое ожидание прибыли при усреднении по спросу.
- математическое ожидание прибыли при усреднении по спросу.