Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выработка оптимальной стратегии в игровой ситуацииСодержание книги
Поиск на нашем сайте
Игрок делает ставку в размере $9,00 и получает возможность четыре раза бросить игровую кость, имеющей на своих гранях числа 1, 2, 3, 4, 5 и 6. Игрок может закончить игру после любого броска, забрав выигрыш, равный удвоенному числу, выпавших во время последнего броска очков. Стоит ли играющему соглашаться на такие условия игры? При положительном ответе разработать стратегию поведения игрока. Попробуем разобраться в описанной игровой ситуации. Прежде всего, представим условия игры в виде таблицы приложения MS Excel на Рис.7.
Рис.7. Представление исходных данных в приложении MS Excel. Очевидно, что если в первом броске выпадет 6 или 5, то игру можно заканчивать, т.к. выигрыш будет превышать сделанную ставку. Правда, во втором случае можно понадеяться на выпадение 6 в последующих бросках. При выпадении в первом броске меньшего, чем 5 числа очков можно, надеясь наудачу в последующих попытках, продолжить игру. С другой стороны, если игрок дошёл до четвёртой попытки, то окончание игры будет безусловным и, возможно, при выпадении малого числа очков, игрок пожалеет, что не прервал игру на более удачных предыдущих попытках. Решение. Очевидно, что ситуация носит вероятностный характер. Поэтому принятие решения: соглашаться или нет на предложенные условия игры, возможно лишь при оценке среднего выигрыша. Поставленная задача относится к задачам вероятностного динамического программирования. Они решаются в соответствии с алгоритмом обратной прогонки [1-3]. Для функции Беллмана введём обозначение
Если всего шагов n, то очевидно, что:
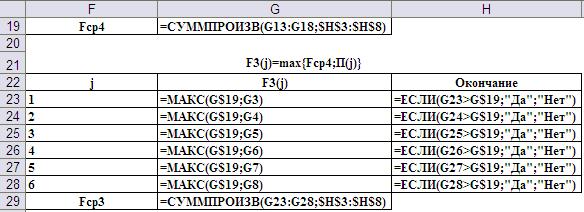
т.к. у последнего шага последующих шагов нет. Для формализации и однотипности действий на каждом шаге удобно считать, что Итак, алгоритм обратной прогонки. Шаг 1-ый, i=4. Его результат представлен таблицей, рассчитанной в MS Excel (Рис.8)
Рис.8. Результат первого шага вычисления функции Беллмана. Данные были автоматически сформированы при вводе в ячейки рабочего листа формул, представленных на Рис.9.
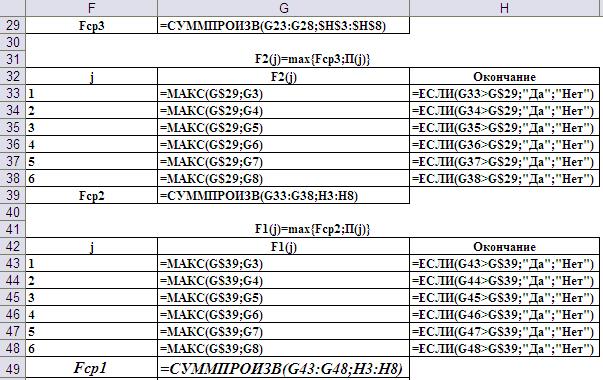
Рис.9. Ввод формул для реализации первого шага. Шаг 2-ой, i=3. Его результаты и ввод формул для реализации представлены на Рис.10 и Рис.11, соответственно.
Рис.10. Результат второго шага вычисления функции Беллмана.
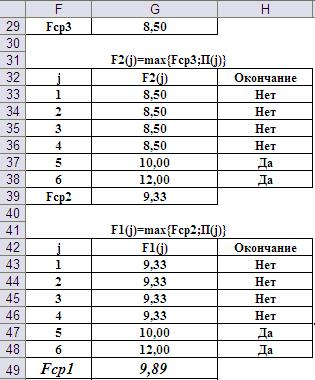
Рис.11. Ввод формул для реализации второго шага. Выполнение третьего и четвёртого шагов показаны на Рис.12 (результаты) и Рис.13 (формулы).
Рис. 12. Результаты расчётов на третьем и четвёртом шагах.
Рис. 13. Ввод формул для выполнения третьего и четвёртого шагов. Итак, в результате реализации алгоритма обратной прогонки получили ответы на оба поставленных вопроса задачи. Во-первых, т.к. Fcp1=9,89 превышает сделанную ставку, равную 9, то условия игры могут быть приняты. Во-вторых, оптимальная стратегия действий игрока на каждом шаге представлена в третьих столбцах таблиц результатов на каждом шаге. При игре их надо просматривать в прямом, а не в обратном, порядке. Организация рабочего листа в приложении MS Excel позволяет ответить и ряд других вопросов. Например, нечистые на руку организаторы игрового бизнеса предлагают играть «краплёными» костями с вероятностью выпадения граней, представленных в таблице:
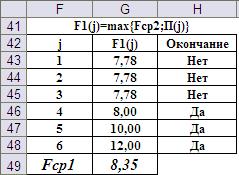
Указанные в таблице вероятностные характеристики игральных костей можно получить за счёт смещения центра тяжести костей. В этом случае Fcp1=8,35 (Рис.14).
Рис. 14. Результат выполнения четвёртого шага при «краплёных» игральных костях. Таким образом, ожидаемый выигрыш при оптимальной стратегии меньше, чем сделанная ставка! Принимать условия игры не следует. Проделанные расчёты можно подкрепить статистическими испытаниями. На Рис.15 показана структура статистической таблицы и результат однократного моделирования при «краплёных» игральных костях.
Рис. 15. Структура таблицы статистических испытаний и результат моделирования при «краплёных» игральных костях. Таблица для моделирования бросков «краплёных» игральных костей показана на Рис.16. Идеология её построения излагалась в предыдущей лабораторной работе.
Рис. 16. Таблица для моделирования бросков «краплёных» игральных костей. Формулы для реализации метода статистических испытаний показаны на Рис.17.
Рис. 17. Ввод формул для реализации метода статистических испытаний. На Рис.17 показаны формулы только для первого бросания игральной кости. Формулы, моделирующие бросания на следующих шагах, идентичны. Поэтому соответствующие столбцы скрыты. Задачи для самостоятельного решения 1. Игра в рулетку. Игрок делает ставку в размере $7,5 и получает возможность несколько раз крутануть рулетку с пятью секторами, помеченными цифрами 1, 2, 3, 4 и 5. Игрок может закончить игру после любого шага, забрав выигрыш, равный удвоенному числу, выпавшему во время последнего вращения рулетки. Секторы рулетки выпадают равновероятно. · Сколько попыток вращения необходимо иметь, чтобы ожидаемый выигрыш превысил сделанную ставку? · Каков будет средний выигрыш, если игрок имеет пять попыток? · Определить оптимальную стратегию игры. · По своему усмотрению сделать выпадения секторов рулетки неравновероятными. Рассчитать средний выигрыш, если игрок имеет пять попыток. Задачу решить формульно, а затем подтвердить правильность решения методом статистических испытаний. Литература 1. Excel, VBA, Internet в экономике и финансах; Гарнаев А.Ю. 2005, Издательство BHV – Санкт – Петербург. 2. Колдаев В.Д. Основы алгоритмизации и программирования: Учебное пособие / Под ред. проф. Л.Г. Гагариной. - М.: ИД «ФОРУМ»: ИНФРА – М, 2008. – 416 с.: ил. – (Профессиональное образование). ISBN 5-8199-0279-3 (ИД «ФОРУМ») ISBN 5-16-0022690-8 (ИНФРА – М) 3. Исследование операций в экономике: учебн. пособие / Под ре. Н.Ш. Кремера. - М.: Маркет ДС, 2007. 4. Минько Э.В. Методы прогнозирования и исследования операций: учеб. пособие/ Э.В.Минько, А.Э.Минько; под ред. А.С.Будагова. - М.: Финансы и статистика; ИНФРА – М, 2010. – 480 с.: ил. ISBN 978-5-279-03417-8 (Финансы и статистика) ISBN 978-5-16-004251-0 (ИНФРА – М) 5. Фомин Г.П. Математические методы и модели в коммерческой деятельности: учебник/Г.П.Фомин. – 3-е изд., перераб. и доп. – М.: Финансы и статистика; ИНФРА – М. – 2009. – 640 с.: ил. ISBN 978-5-279-03353-9 (Финансы и статистика) ISBN 978-5-16-003660-1 (ИНФРА – М) Содержание Лабораторная работа № 1. Методы линейной оптимизации…………………3 Лабораторная работа № 2. Транспортные задачи, логистика, задачи о назначениях…………………………………………………….………….………21 Лабораторная работа № 3. Комплексное и многопериодное планирование……………………………………………..…………………..…………42 Лабораторная работа № 4. Распределение средств на рекламу, планирование рекламной кампании………………………………………………………..65 Лабораторная работа № 5. Инвестирование предприятий…………………..76 Лабораторная работа № 6. Оптимизация на графах……….…………………86 Лабораторная работа № 7. Принятие решений в условиях риска……………………………………………………….………..……………98 Лабораторная работа № 8. Метод статистических испытаний…………………………………………………..……………...….……104 Лабораторная работа № 9. Применение метода статистических испытаний в проектном анализе и игровых моделях………………..…………………120 Литература. …………………….……………………………….………………135
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.72.244 (0.008 с.) |


 , означающее средний выигрыш на i-ом шаге при условии, что выпало j очков. Очевидно, её нужно вычислять как максимум между текущим выигрышем при выпадении j очков
, означающее средний выигрыш на i-ом шаге при условии, что выпало j очков. Очевидно, её нужно вычислять как максимум между текущим выигрышем при выпадении j очков  и средним значением функции Беллмана на последующем шаге
и средним значением функции Беллмана на последующем шаге 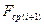 , т.е.
, т.е.
 ,
, .
.