Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение оптимальных объёмов закупок.Содержание книги
Поиск на нашем сайте
1. Найти оптимальные объёмы закупок по изложенным правилам, цены на товар соответствуют таблице
а спрос на товар подчиняется нормальному закону распределения со средним значением 60 и средним квадратическим отклонением 5. Рекомендации: a) считать, что объём товара измеряется целыми числами; b) при расчёте диапазона спроса использовать закон трёх сигм. 2. Для правила максимальной ожидаемой прибыли построить графики зависимости
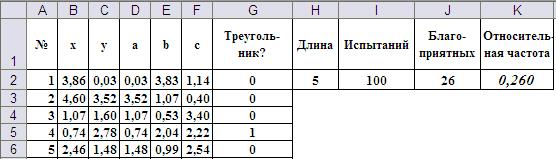
Лабораторная работа №8 Метод статистических испытаний В данной лабораторной работе изучается реализация метода статистических испытаний и его применение для решения задач по теории вероятностей. Теоретические основы В задачах оптимизации, когда необходимо учитывать некоторый случайный фактор (элемент или явление), который невозможно описать аналитически, используют метод моделирования, называемый методом статистических испытаний или методом Монте-Карло [4,5]. С помощью этого метода может быть решена любая вероятностная задача. Однако использовать его целесообразно в том случае, если решить задачу этим методом проще, чем любым другим. Суть метода состоит в том, что вместо описания случайных явлений аналитическими зависимостями проводится розыгрыш случайного явления с помощью некоторой процедуры, которая дает случайный результат. С помощью розыгрыша получают одну реализацию случайного явления. Осуществляя многократно такой розыгрыш, накапливают статистический материал (множество реализаций случайной величины), который можно обрабатывать статистическими методами. Рассмотрим этот метод на примерах. Пример 1. Трость длиной L разламывается на три части. Расстояния от начала трости до двух точек перелома – непрерывные случайные величины с равномерным законом распределения. Найти вероятность того, что из получившихся частей можно собрать треугольник. В теории вероятностей эта задачу называют задачей о «сломанной трости». Эту задачу можно решить методами теории вероятности. Обозначим через x и y расстояния от левого конца трости первой и второй точек перелома (Рис.1).
Рис.1. Условные обозначения для задачи о «сломанной трости»
Тогда длины сторон возможного треугольника выражаются через L, x и y следующим образом
Длины сторон треугольника должны удовлетворять условию: сумма длин двух любых сторон больше (или в вырожденном случае равна) длине третьей стороны. Таким образом, имеем систему неравенств
После подстановки длин сторон треугольника через L, x и y получим
Решение полученной системы неравенств можно наглядно иллюстрировать на двухкоординатной плоскости. (Рис.2). Т.к. величины x и y имеют равномерное распределение на отрезке [0; L], то множеству точек со всевозможными координатами (x;y) соответствует квадрат OPRS со стороной L. Тогда точки, координаты которых удовлетворяют составленной системе неравенств с учётом условия
Рис. 2. Графическая иллюстрация решения задачи Примера 1. Искомая вероятность равна доле суммарной площади треугольников от площади квадрата OPRS
Решим эту задачу методом статистических испытаний. Для этого в приложении MS Excel создадим таблицу, как показано на Рис. 3.
Рис.3. Структура таблицы для решения задачи Примера 1 методом статистических испытаний. На Рис.4a-b показан ввод формул в ячейки листа для решения задачи Примера 1 методом статистических испытаний.
Рис.4a. Ввод формул для реализации случайного перелома трости и проверки возможности формирования треугольника.
Рис.4b. Ввод формул для обработки серии испытаний. Моделирование координат точек перелома x и y осуществляется по формулам «=Длина*СЛЧИС()»(см. формулы в ячейках B2 и C2). Встроенная функция СЛЧИС() генерирует случайную величину, равномерно распределённую на отрезке [0;1]. Выбор в качестве стороны a минимального значения
позволяет учесть оба случая, когда С помощью логических суперпозиции логических функций ЕСЛИ() и И() в ячейке G2 обеспечивается поверка возможности собрать треугольник из фрагментов трости. При этом возможность кодируется единицей, а невозможность нулём. Такая кодировка позволяет просто подсчитать число благоприятных исходов с помощью функции СУММ() (ячейка J2)
Формулы в ячейках H2, I2, J2 и K2 обеспечивают подсчёт общего числа испытаний, числа благоприятных исходов и их долю в общем числе испытаний. При каждом нажатии функциональной клавиши F9 Excel пересчитывает функции СЛЧИС() и, таким образом, моделирует новую серию испытаний. В каждой серии получается новое значение вероятности (на Рис. 3 она равна 0,26). В качестве оценки вероятности берут среднее арифметическое от нескольких серий. Усреднение десяти выборочных значений представлено в таблице:
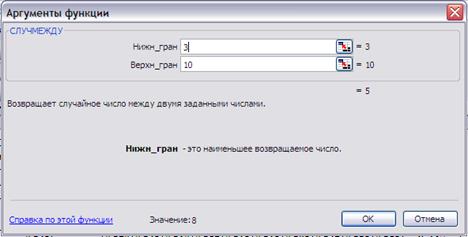
Полученное среднее значение 0,247 близко к значению, рассчитанному теоретически 0,250. На практике такой точности вполне достаточно. Таким образом, алгоритм метода статистических испытаний сводится к следующему. · Определить, что собой будет представлять испытание или розыгрыш. · Определить, какое испытание является успешным, а какое– нет. · Провести большое количество испытаний. · Обработать полученные результаты статистическими методами и рассчитать статистические оценки искомых величин. При проведении статистических испытаний необходимо воспроизводить случайные величины с нужным законом распределения. Приложение MS Excel имеет для этого достаточное число средств. Простейшими является функция СЛЧИС() и СЛУЧМЕЖДУ(a,b). Первая функция генерирует случайное число с равномерным законом распределения на полуинтервале [0;1) (Рис. 5), вторая - случайное число с равномерным законом распределения на интервале (a;b) (Рис. 6).
Рис.5. Конструктор функции СЛЧИС().
Рис.6. Конструктор функции СЛУЧМЕЖДУ(a;b).
Кроме того, MS Excel располагает надстройкой «Пакет анализа», которая содержит генератор случайных величин с различными функциями распределения (Рис.7).
Рис.7. Диалоговое окно генератора случайных чисел. Перечисленные средства предоставляют практически неограниченные возможности по моделированию случайных величин. Моделирование события. Пусть необходимо смоделировать появление некоторого события А, вероятность наступления которого равняется Р(А)=Р. Это можно смоделировать суперпозицией функций: =ЕСЛИ(СЛЧИС()<=P; “произошло событие А”; “событие А не произошло”)
Рис. 8. Вероятность наступления события А
Моделирование группы несовместимых событий. Пусть есть группа несовместимых событий А1, А2,..,.Аk. Известны вероятности наступления событий Р(А1), Р(А2),..., Р(Аk). Тогда из-за несовместимости испытаний
Рис. 9. Вероятности наступления группы несовместимых событий Если число, сгенерированное функцией СЛЧИС() попало в i-ый интервал, то произошло событие Аi. Моделирование условного события. Моделирование условного события B, которое происходит при условии, что наступило событие A с вероятностью Р(B/A), показано на рис. 10. Сначала моделируем событие A. Если событие A происходит, то моделируем наступление события B, если имеем
Рис. 10. Моделирование условного события B
Рассмотрим пример на моделирование условных событий. Пример 2. В сборочный цех поступили детали с трех предприятий. На первом предприятии изготовлено 51% деталей от их общего количества, на втором предприятии 24% и на третьем 25%. При этом на первом предприятии было изготовлено 90% деталей первого сорта, на втором 80% и на третьем 70%. a) Какова вероятность того, что взятая наугад деталь окажется первого сорта? b) Какова условная вероятность того, что если взятая наугад деталь оказалась бракованной, она была изготовлена на первом предприятии?
Решение: Сначала решим задачу по формулам, используя соответствующие формулы теории вероятностей. a) Пусть A - cобытие, состоящее в том, что взятая деталь окажется первого сорта, а H1, H2 и H3 - гипотезы, что она изготовлена соответственно на 1, 2 и 3 предприятии. Вероятности этих гипотез соответственно равны:
Далее, из условия задачи следует, что:
Используя формулу полной вероятности, получим искомую вероятность
b) Изделие выбирается наудачу из всей произведённой продукции и оказывается бракованным. Рассмотрим три гипотезы: Hi – деталь изготовлена на i-ом предприятии i=1,2,3. Вероятности этих событий даны:
Пусть изделие оказалось бракованным. Условные вероятности этого по отдельным предприятиям:
Тогда искомая условная вероятность считается как доля бракованных изделий первого предприятия относительно общего числа брака:
Итак, задача решена. Её решение потребовало знаний соответствующих разделов теории вероятностей, в частности, формул расчёта полной и условной вероятностей. При решении задачи методом статистических испытаний этих соотношений можно не знать. Исходные данные рационально организовать, как показано на Рис.11. Таблицы вероятностей дополнены тремя столбцами «Просмотр», «Результат» и «Номер события». Это необходимо для реализации моделирования группы несовместимых событий и моделирования условных событий. На Рис.12 данный фрагмент листа представлен в режиме показа формул. В столбце «Просмотр» сформирована сумма вероятностей нарастающим итогом. Тем самым формируются границы событий согласно идее, представленной на Рис.9. Моделирование наступления одного из несовместимых событий реализуется по следующей схеме: · моделирование с помощью функции СЛЧИС() случайной величины с равномерным законом распределения на полуинтервале [0;1); · поиск полученного значения с помощью функции ПРОСМОТР() в столбце «Просмотр» и извлечение из таблицы названия события из столбца «Результат» или его условного номера из столбца «Номер события».
Рис. 11. Организация таблиц исходных данных
Рис. 12. Ввод формул в исходные таблицы данных
На Рис. 13-14a)-c) показаны, соответственно, общий вид таблицы статистического моделирования и введённые формулы. Выбор значений условных вероятностей брака и деталей первого сорта из таблиц осуществляется с помощью суперпозиции функций ПРОСМОТР() и СМЕЩ(). Первая осуществляет непосредственно выбор из таблицы, а обращение к нужной таблице в зависимости от номера смоделированного предприятия происходит с помощью функции СМЕЩ(). Для этого таблицы условных вероятностей должны располагаться с одинаковым шагом (в данном случае с шагом 5).
Рис. 13. Общий вид таблицы статистических испытаний
a)
b)
c) Рис. 14. Ввод формул в таблицу статистических испытаний Усреднение результатов проведённого моделирования в соответствии с пунктами задания Примера 2 приведено в таблицах:
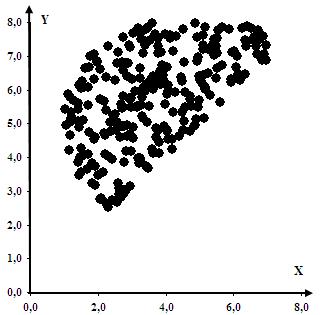
Отмечаем близость полученных результатов моделирования к теоретическим расчётам. Метод статистических испытаний может успешно применяться для решения многих других задач, имеющих детерминистский характер. В частности, этим методом наглядно, правда приблизительно, решаются задачи линейного и нелинейного программирования, задачи построения множеств точек, координаты которых удовлетворяют системе неравенств. Алгоритм решения сводится к следующему: · моделирование случайного множества точек в n-мерном пространстве; · выбор из сформированного множества подмножества точек, координаты которых удовлетворяют системе ограничений; · выбор из полученного подмножества за счёт сортировки в нужном порядке точки, с максимальным или минимальным значением целевой функции; · построение для двухмерного случая области ограничения на переменные. На Рис. 15 показана полученная по этому алгоритму область ограничения на переменные X и Y при решении следующей нелинейной оптимизационной задачи:
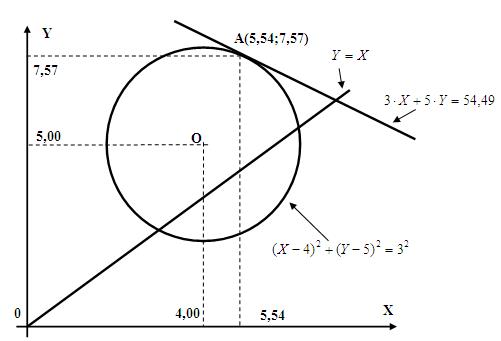
Оптимальное решение достигается в точке с координатами: X=5,53; Y=7,54, в которой целевая функция принимает значение Zmax=54,28. Точное решение, полученное с помощью средства «Поиск решения»: X=5,54; Y=7,57, Zmax=54,49. Иллюстрация точного решения показана на Рис.16. Как видим, погрешность удовлетворяет практическим требованиям.
Рис. 15. Область ограничений, построенная методом статистических испытаний.
Рис. 16. Графическая иллюстрация точного решения задачи нелинейной оптимизации.
Задачи для самостоятельного решения 1. Организация страховой фирмы. При наступлении страхового случая страховая компания выплачивает страховую премию в размере
Задачу решить формульно и методом статистических испытаний. Сравнить результаты. 2. Сдача зачёта. По некоторому предмету студент выучил 20 вопросов из 30. Преподаватель наугад выбирает три вопроса. С какой вероятностью студент получит зачёт, если преподаватель ставит зачёт за знание не менее двух вопросов. Задачу решить формульно и методом статистических испытаний. Сравнить результаты.
3. Задача линейного программирования. Решить задачу линейного программирования.
Решить задачу методом статистических испытаний и с помощью средства «Поиск решения». Сравнить результаты.
Лабораторная работа №9 Применение метода статистических испытаний В данной лабораторной работе рассматривается применение метода статистических испытаний для решения задач проектного анализа и игровых моделей. Теоретические основы Проектный анализ Пример. Фирма «Гигант» разрабатывает инвестиционный проект производства банковских сейфов нового поколения. Инвестиции в данный проект намечено производить в три этапа. 1-ый этап. В начальный момент времени необходимо затратить $500 тыс. на проведение маркетингового исследования рынка. 2-ой этап. Если в результате проведённого исследования обнаружено, что потенциал рынка достаточно высок, то в следующий момент времени фирма «Гигант» инвестирует дополнительно $1000 тыс. на разработку и создание опытных образцов сейфов, подлежащих экспертизе в Специальном центре по безопасности банков, специалисты которого решают вопрос о размещении заказа в данной фирме. 3-ий этап. Если экспертная комиссия вынесла положительное решение о представленных сейфах, то фирма начинает строительство нового предприятия и организацию серийного производства сейфов, для чего ей потребуется ещё $10000 тыс. Реализация данной стадии, по оценкам аналитиков и менеджеров проекта, обеспечит возможность генерирования проектом притоков наличности в течение четырёх лет. Величина притоков зависит от того. Насколько хорошо сейф принят на рынке. Для анализа и оценки риска рассматриваемого многостадийного процесса целесообразно использовать метод дерева решений (Рис.1)..
Рис.1. Дерево решения для проекта производства сейфов. Исходим из предположения, что очередное решение об инвестировании принимается фирмой в конце года. Каждое «разветвление» означает точку принятия решения, либо очередной этап. Число, записанное внутри вершины графа, означает размер инвестиций или размер притока наличностей. Очевидно, что инвестиции записываются отрицательными числами, а притоки наличностей – положительными. Числа на дугах дерева означают вероятности переходов в различные состояния. Так, если фирма «Гигант» решает реализовывать проект в момент времени t=0, то она должна потратить $500 тыс. на проведение маркетингового исследования. По оценкам менеджеров компании, вероятность благоприятного результата равна 0,8, а вероятность получения неблагоприятного результата – 0,2. На дереве решений это отображается самой левой вершиной и двумя дугами, выходящих из неё (момент времени t=0). Если по результатам маркетингового исследования руководство фирмы приходит к оптимистическому заключению о потенциале рынка, то в момент времени t=1 необходимо потратить ещё $1000 тыс. на изготовление экспериментального образца сейфа. Менеджеры фирмы оценивают вероятность положительного исхода в 0,6, а вероятность отрицательного исхода – 0,4 (вершина с размером инвестиций -1000 и дуги 0,6 и 0,4 в момент времени t=1 на дереве решений). В случае, если экспертный совет находит данную модель сейфа привлекательной, фирма в момент времени t=2 должна израсходовать ещё $10000 тыс. на строительство нового предприятия и организации серийного производства сейфов. Если фирма «Гигант» приступает к производству сейфов, то операционные потоки наличности в течение четырёхлетнего срока жизни проекта зависят от того, насколько хорошо продукт будет «принят» рынком. По оценкам маркетологов, вероятность того, что рынок положительно воспримет продукт, составляет 0,3, и в этом случае чистые притоки наличности должны составлять около $10000 тыс. ежегодно. Вероятности того, что притоки наличности будут составлять около $4000 тыс. и -$2000 тыс. в год, равны 0,4 и 0,3 соответственно. Эти ожидаемые потоки наличности на дереве решений показаны с третьего года по шестой. Вероятность реализации пути от начальной вершины до выхода равна произведению вероятностей дуг на этом пути. В предположении, что средняя учётная банковская ставка составляет 11,5%, рассчитаем чистый дисконтированный доход (
где:
Затем, умножая значения чистого дисконтированного дохода
Расчёты по изложенной методике реализованы в приложении MS Excel (Рис.2). Ввод формул в ячейки рабочего листа не показан в силу их простоты.
Рис.2. Результаты расчётов для проекта производства сейфов. Поскольку значение ожидаемого чистого дисконтированного дохода проекта производства сейфов оказалось отрицательным (NPV=-$338 тыс.), то можно предположить, что фирма «Гигант» должна отторгнуть этот инвестиционный проект. Так как результат зависит от величины учётной банковской ставки, имеет смысл поставить вопрос о нахождении величины банковской ставки, при которой ожидаемый чистый дисконтированный доход проекта будет равен нулю. Это будут граничная учётная ставка: если реальная ставка будет меньше, проект следует принять, а если больше – отвергнуть. Расчёт граничной учётной ставки можно провести с помощью средства «Поиск решений». На Рис.3 показаны установка опций и результаты расчёта.
Рис.3. Расчёт граничной учётной ставки. Итак, граничная учётная ставка равна 8,7%. Данная задача может быть успешно решена методом статистических испытаний. Для этого необходимо осуществить формализованное описание структуры дерева и его количественных характеристик. Возможный вариант этого заключается в следующем. Каждой вершине дерева ставится в соответствие таблица вида
Каждая таблица имеет номер в виде «Год/Путь». Формально он не используется, но удобен для описания связей между вершинами. Информационная часть таблицы содержит данные о размере инвестиции или денежном потоке, вероятностях возможных решений, номеров решений и адресов последующих вершин, а точнее таблиц, соответствующих последующим вершинам. Адреса представлены относительными смещениями по строкам и столбцам. Для удобства заполнения таблиц их рационально расположить в соответствии со структурой дерева (Рис.4).
Рис.4. Расположение таблиц вершин дерева. На нулевом году проекта моделируется принятие одного из двух возможных решений. На последующих годах моделируется одно возможных в соответствии с данными текущей вершины. При этом на каждом году идёт накопление суммы инвестиций или потоков с учётом дисконтирующих коэффициентов. Моделирование возможного пути осуществляется многократно, например 500, результаты (накопленная сумма) усредняются, а затем статистически обрабатываются, как это требует алгоритм метода статистических испытаний. На Рис.5 показана структура таблицы статистических испытаний, а на Рис.6 – ввод формул в таблицу. Часть строк и столбцов скрыта.
Рис.5. Структура таблицы статистических испытаний.
Рис.6. Ввод формул в таблицу статистических испытаний. Результаты статистического моделирования соответствуют результатам детерминированного расчёта. Реализация статистического моделирования в данном случае, возможно, покажется более сложной, чем детерминированные расчёты. Однако имеет смысл его осуществить. Приобретённый опыт будет весьма полезен при решении задач, где имеют место вероятностные переходы из одних состояний в другие, например, в системах массового обслуживания.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 408; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.158.111 (0.016 с.) |

 ,
, и прибыли
и прибыли  . При этом считать, цену продажи фиксированной
. При этом считать, цену продажи фиксированной  , а диапазон цены закупки
, а диапазон цены закупки  .
.
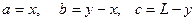


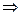

 , принадлежат области, ограниченной треугольником ABC. Если провести аналогичные рассуждения для случая
, принадлежат области, ограниченной треугольником ABC. Если провести аналогичные рассуждения для случая 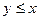 , то получим треугольник CDE.
, то получим треугольник CDE.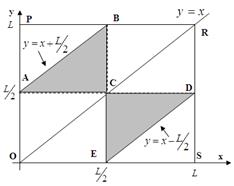
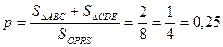

 м
м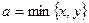 и расчёт сторон b и c по формулам
и расчёт сторон b и c по формулам




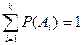 . На отрезке [0, 1] отложим эти вероятности (Рис. 9).
. На отрезке [0, 1] отложим эти вероятности (Рис. 9).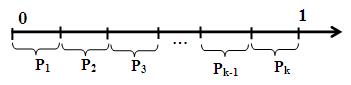
 , то не моделируем наступление события B.
, то не моделируем наступление события B.















 ден. ед. Клиент выкупает страховой полис на год страхования. Произвести расчёт стоимости страхового полиса
ден. ед. Клиент выкупает страховой полис на год страхования. Произвести расчёт стоимости страхового полиса  в предположении, что договоры заключат N человек, вероятность страхового случая равна
в предположении, что договоры заключат N человек, вероятность страхового случая равна  , гарантия выплат страховых премий равна
, гарантия выплат страховых премий равна  , а сбор компании должен превышать ожидаемую сумму выплат на D %. Исходные данные приведены в таблице:
, а сбор компании должен превышать ожидаемую сумму выплат на D %. Исходные данные приведены в таблице: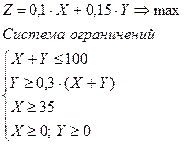

 ) по каждому из вариантов, представленных деревом решений
) по каждому из вариантов, представленных деревом решений ,
, - величина инвестиции (притока наличности) при i-ом варианте решения на j-ом году проекта;
- величина инвестиции (притока наличности) при i-ом варианте решения на j-ом году проекта; - дисконтирующий множитель для j-ого года;
- дисконтирующий множитель для j-ого года; - учётная банковская ставка.
- учётная банковская ставка. , получаем ожидаемый чистый дисконтированный доход инвестиционного проекта.
, получаем ожидаемый чистый дисконтированный доход инвестиционного проекта. ,
,