Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача № 1 Проверка прочности ступенчатого стержня при деформации растяжение и сжатие.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Содержание
Задача № 2 Расчет оптимального сечения ступенчатого стержня при деформации растяжение и сжатие. Задание: Определить оптимальный диаметр сечения круглого стержня на каждом участке по условию прочности. Определить продольные деформации, возникающие на каждом участке стержня. Стержень изготовлен из стали: Е = 2*105 МПа; σТ = 240 МПа. Допускаемый коэффициент запаса статической прочности [n] выбрать самостоятельно ([n]= 1,2…1,8). Весом стержня пренебречь. Схема стержня приведена на рис. 2.
Исходные данные: F1=17 кН; F2=28 кН; F3=7кН; l 1=130 см=1,3 м; l 2=140 см=1,4 м; l 3=65 см=0,65 м. Решение: Для определения продольной силы используем метод сечений. Эпюру продольных сил необходимо строим, руководствуясь правилом: продольная сила в любом сечении стержня равна алгебраической сумме проекций всех внешних сил, расположенных по одну сторону от сечения на ось стержня. Продольная сила считается положительной, если она соответствует деформации растяжения (направлена от сечения) и отрицательной, если она вызывает сжатие (направлена к сечению). 1.Разобьем стержень на отдельные участки, начиная от свободного конца. Границы участков определяются точками приложения внешних сил. Всего по длине стержня в данной задаче будет три участка. Проведя сечения и отбрасывая левые части стержня, можно определить продольные силы в его поперечных сечениях без вычисления опорных реакций в заделке. 1 участок (сечение 1-1): NI = -F3 = -7 кН. на первом участке осуществляется деформация сжатия. 2 участок (сечение 2-2): N2 = -F3 +F2 = -7+28=21 кН. на втором участке осуществляется деформация растяжения. 3 участок (сечение 3-3) N3 =-F3 +F2+F1 = -7+28+17=38 кН. на третьем участке осуществляется деформация растяжения. Таким образом, в заделке действует реакция равная N3 =38 кН. Эпюра продольных сил показана на рис.1. Эпюру продольных сил строим в масштабе 2. Допускаемое напряжение вычисляем по формуле: Допускаемые напряжения при сжатии и растяжении для пластичного материала, при условии, что коэффициент запаса n=1,8.
3. Требуемая площадь сечения определяется из формулы условия прочности на растяжения.
Площадь круглого сечения А= 1 участок:
Принимаем d1=0,09м, А1= 2 участок:
Принимаем d2=0,015 м, А2= 3 участок:
Принимаем d1=0,02м, А3= Удлинения (укорочения) части стержня определяем по формуле Укорочение 1 участка Удлинение 2 участка Удлинение 3 участка В правом конце стержня заделка, перемещение в этом конце отсутствует. Поэтому построение эпюры смещения стержня необходимо строить, начиная с левого конца. На третьем участке смещение изменяется от нуля до на втором участке: от
на первом участке: от до Эпюры смещения строим в масштабе:
Ответ: Полное удлинение стержня составило
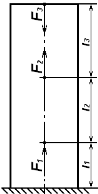
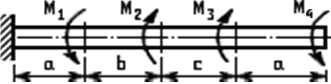
Задача № 3 Расчет статически определимой стержневой системы, Задача № 4 Расчет вала на прочность и жесткость. Задание: Определить диаметры ступенчатого вала из условия прочности и жесткости на кручение. Определить угол закручивания вала. Вал изготовлен из стали: [Θ] = 1,75 *10-2 рад/м, G = 8 *1010 Па Схема вала приведена на рис. 4.
Исходные данные: а =1,4м; b=0,6м, c=0,6м, М1 =360Н*м; М2 = 400Н*м; М3 = 400Н*м; М4 = 500Н*м; [t] = 55 Мпа. Решение. 1. Определение внутренних крутящих моментов по участкам. Для определения знака крутящего момента примем следующее правило: если смотреть на отсеченную часть бруса со стороны внешней нормали к сечению, то момент сечении будет положителен в том случае, когда сумма внешних скручивавших моментов поворачивает отсеченную часть бруса по часовой стрелке, и отрицателен при повороте части бруса в противоположном направлении. Неизвестный момент М5 в заделке найдем из уравнения равновесия для всего вала. Условно примем направление момента М5 за отрицательное. Тогда уравнение равновесия принимает вид -М1 +М2 +М3 -М4-М5 = 0 Из решения этого уравнения получим М5 =- М1 +М2 +М3 -М4=-360+400+400-500= -60Н*м. Для построения эпюры крутящих моментов применяем метод сечений к каждому участку вала в отдельности (следует заметить, что построение эпюры крутящих моментов совершенно аналогично построению эпюры продольных сил). Крутящие моменты в сечениях определяются как алгебраические суммы внешних моментов, приложенных по одну сторону от сечения. Определим крутящие моменты на каждом участке, проведя последовательно сечения на четырехучастках вала и рассмотрим равновесие соответствующих оставшихся правых частей. В сечении 1-1: В сечении 2-2: В сечении 3-3: В сечении 4-4:
По полученным данным строим эпюру крутящих моментов, откладывая по вертикальной оси значения моментов. Отрицательные моменты откладываем вниз по осевой линии (рис. 4). Эпюру моментов строим в масштабе 2. По найденным значениям крутящих моментов из расчетов на прочность и жесткость в каждом сечении определим диаметры валов. Расчет на прочность ведется по допускаемому напряжению при кручении
где
По формуле определим диаметры для всех сечений. Сечение 1-1: Сечение 2-2: Сечение 3-3: Сечение 4-4:
3. Расчет на жесткость ведется по допускаемому относительному углу закручиванию В соответствии с формулой определим диаметр вала из условия жесткости
По формуле определим диаметры для всех участков. Сечение 1-1: Сечение 2-2: Сечение 3-3: Сечение 4-4: 4. В соответствии с расчетами на прочность и жесткость выбираем наибольшее значение диаметров для каждого участка. В результате получим следующие значения: 5. Абсолютные углы закручивания для каждого участка можно определить по формуле Полярные моменты инерции для каждого сечения Сечение 1-1: Сечение 2-2: Сечение 3-3: Сечение 4-4: Далее определим углы закручивания.
Строим эпюру углов закручивания для всего вала (рис. 4). За начало координат выбран крайний левый конец бруса (сечение D). В пределах каждого из участков бруса эпюра линейна, поэтому достаточно знать углы поворота только для граничных сечений участков. В сечении от Е до D полный угол закручивания вала равен
В сечении от Е до С полный угол закручивания вала равен
В сечении от Е до В полный угол закручивания вала равен
В сечении от Е до А полный угол закручивания вала равен
Ординаты этой эпюры дают значения углов поворота соответствующих поперечных сечений вала. Эпюру углов поворота строим в масштабе
Ответ:
Список литературы 1. Сопротивление материалов: учебное пособие для вузов/ Н.Н.Вассерман и др. - Пермь: Изд-ва ПНИПУ, 2011 – 364 с. 2. Прикладная механика: Учеб. Для вузов/ В.В.Джамай, Ю.Н.Дроздов, Е.А.Самойлов и др. – М. Дрофа, 2004. – 414 с. 3. Феодосьев В.И. Сопротивление материалов. М.: МГТУ им. Н.Э. Баумана, 1999 – 592 с.
Содержание
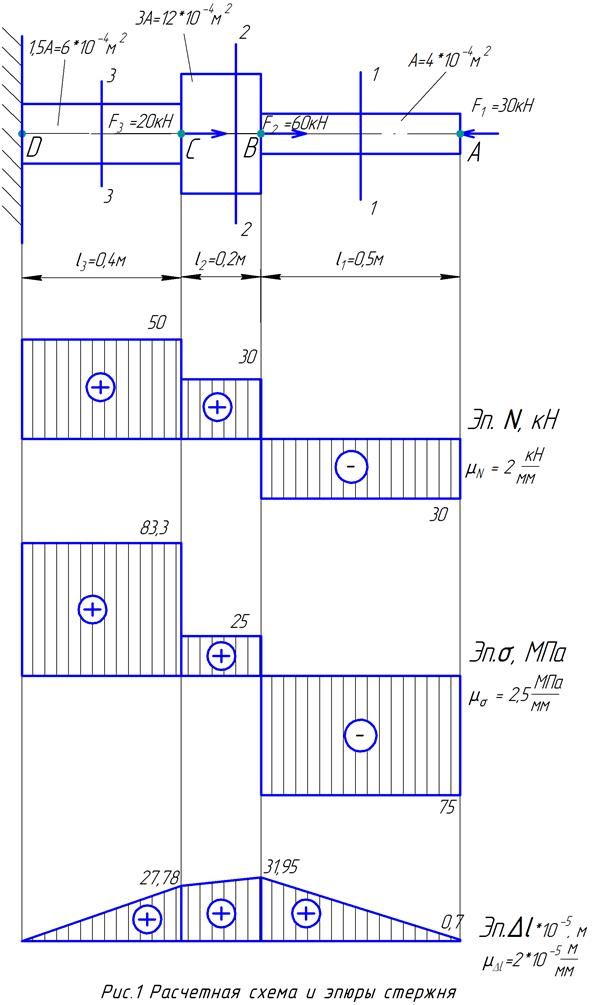
Задача № 1 Проверка прочности ступенчатого стержня при деформации растяжение и сжатие. Задание: Оценить прочность ступенчатого стержня из хрупкого материала. Определить его деформацию. Стержень изготовлен из чугуна: Е = 1,2*105 МПа; σвр = 113 МПа; σвсж = 490 МПа. Допускаемый коэффициент запаса статической прочности [n] выбрать самостоятельно (в данной задаче принимаем [n]= 1,2…1,8). Весом стержня пренебречь. Схема стержня приведена на рис. 1.
Исходные данные: l 1=0,5м; l 2=0,2м; l 3=0,4м; А=4*10-4м2; А1=А= = 4*10-4м2; А2=3А=12*10-4м2; А3=1,5А=6*10-4м2; F1=30кН; F2=60кН; F3=20кН. Решение. Разобьем стержень на отдельные участки, начиная от свободного конца. Границы участков определяются точками приложения внешних сил или местами изменения размеров поперечного сечения. Всего по длине стержня в данной задаче будет три участка. Проведя сечения и отбрасывая левые части стержня, можно определить продольные силы в его поперечных сечениях без вычисления опорных реакций в заделке. Для того, чтобы определить усилие NI, проводим сечения в пределах первого участка. Рассмотрим равновесие оставшейся правой части стержня. Из уравнения равновесия оставшейся правой части выразим внутреннюю продольную силу NI через внешние силы, приложенные к оставленной части NI =- F1 = -30 кН Так как положительное направление совпадает с деформацией растяжения, то знак минус означает, что на первом участке осуществляется деформация сжатия. Аналогично находим внутреннее усилие NII, действующее на втором участке. Для этого проводим произвольное сечение на втором участке и рассматриваем равновесие оставшейся правой части стержня. Уравнение равновесия в проекции на ось стержня для второго участка -F1 + F2 -NII = 0 Решая это уравнение, получим NII = -F1 -F2 = -30+60 = 30 кН. на втором участке осуществляется деформация растяжения. Для того, чтобы определить внутреннее усилие NIII, действующее на третьем участке рассмотрим равновесие оставшейся части стержня. -F1 +F2 + F3 – NIII = 0. Решая это уравнение, получим NIII =-F1 + F2 +F3 = -30+60 +20=50 кН. Таким образом, в заделке действует реакция равная NIII =50 кН. на третьем участке осуществляется деформация растяжения. Эпюра продольных сил показана на рис.1. Эпюру продольных сил строим в масштабе Чтобы определить напряжение в поперечных сечениях бруса, нужно разделить числовые значения продольных сил на площади этих сечений. Для первого участка
Допускаемые напряжения при сжатии, при условии, что коэффициент запаса n=1,2
Условие прочности для первого участка выполняется Недогруз конструкции на первом участке составил
Для сечения 2-2: На втором участке деформация растяжения. Допускаемые напряжения при растяжении, при условии, что коэффициент запаса n=1,2
Условие прочности для первого участка выполняется Недогруз конструкции на втором участке составил
Для сечения 3-3: На третьем участке деформация растяжения. Допускаемые напряжения при растяжении Условие прочности для третьего участка выполняется Недогруз конструкции на третьем участке составил
Эпюра нормальных напряжений по длине бруса показана на рис. 1. Эпюры нормальных напряжений строим в масштабе:
укорочение участков бруса определяются по формуле
где
укорочение первого участка
удлинение второго участка
удлинение третьего участка
В левом конце стержня заделка, перемещение в этом конце отсутствует. Поэтому построение эпюры деформации стержня необходимо строить, начиная с левого конца. На третьем участке деформация изменяется от нуля до на втором от до на первом от до Эпюры смещения строим в масштабе:
Ответ: Полное удлинение бруса составило
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 3855; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.214.78 (0.009 с.) |

 =
=  .
. .
. =240/1,8=133,3 Мпа
=240/1,8=133,3 Мпа Þ
Þ 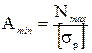






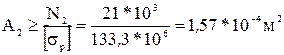







 ,где
,где  – соответственно длина участка, внутреннее усилие, площадь поперечного сечения, Е –модуль упругости материала.
– соответственно длина участка, внутреннее усилие, площадь поперечного сечения, Е –модуль упругости материала. .
.
 .
. =7,87*10-4 м;
=7,87*10-4 м;  =16,17*10-4 м;
=16,17*10-4 м;  16,17*10-4 м
16,17*10-4 м  7,87*10-4 +8,3*10-4 -3,55*10-4=12,62*10-4 м.
7,87*10-4 +8,3*10-4 -3,55*10-4=12,62*10-4 м. =
=  .
. 12,62*10-4м.
12,62*10-4м.
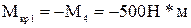 .
.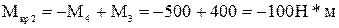 .
.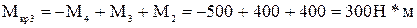
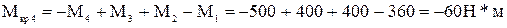
 =
= 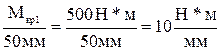 .
.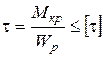
 –крутящий момент, действующий в сечении бруса;
–крутящий момент, действующий в сечении бруса;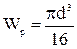 –полярный момент сопротивления для круглого сечения,
–полярный момент сопротивления для круглого сечения, 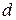 –диаметр вала. Из формулы выразим диаметр
–диаметр вала. Из формулы выразим диаметр 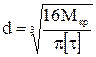
 0,0359м, принимаем d1=0,036м.
0,0359м, принимаем d1=0,036м. 0,021м, принимаем d2=0,022м.
0,021м, принимаем d2=0,022м. 0,0303м, принимаем d1=0,032м.
0,0303м, принимаем d1=0,032м.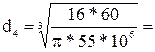 0,0177м, принимаем d4=0,018м.
0,0177м, принимаем d4=0,018м.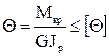 , где
, где  –полярный момент сопротивления круглого сечения.
–полярный момент сопротивления круглого сечения.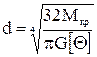
 0,0437м, принимаем d1=0,045м.
0,0437м, принимаем d1=0,045м.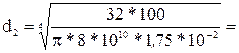 0,0292м, принимаем d2=0,03м.
0,0292м, принимаем d2=0,03м.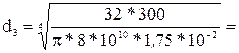 0,0384м, принимаем d1=0,04м.
0,0384м, принимаем d1=0,04м.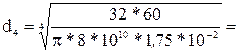 0,0257м, принимаем d4=0,026м.
0,0257м, принимаем d4=0,026м.
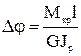 , где
, где 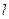 – длина участка.
– длина участка.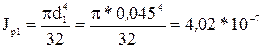 м4;
м4;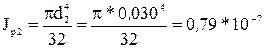 м4.
м4.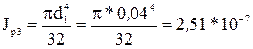 м4;
м4; м4.
м4. = -0,0218 рад – угол поворота сечения В относительно сечения А (или угол закручивания участка АВ).
= -0,0218 рад – угол поворота сечения В относительно сечения А (или угол закручивания участка АВ).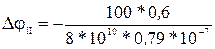 = -0,0095 рад – угол поворота сечения С относительно сечения В (или угол закручивания участка ВС).
= -0,0095 рад – угол поворота сечения С относительно сечения В (или угол закручивания участка ВС).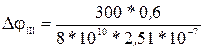 = 0,009 рад – угол поворота сечения D относительно сечения C (или угол закручивания участка CD).
= 0,009 рад – угол поворота сечения D относительно сечения C (или угол закручивания участка CD).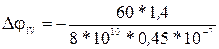 =- 0,0233 рад – угол поворота сечения Е относительно сечения D (или угол закручивания участка DЕ).
=- 0,0233 рад – угол поворота сечения Е относительно сечения D (или угол закручивания участка DЕ).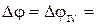 -0,0233 рад;
-0,0233 рад;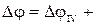
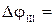 -0,0233+0,009=-0,0143 рад;
-0,0233+0,009=-0,0143 рад;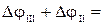 - 0,0233+0,009-0,0095=-0,0238 рад;
- 0,0233+0,009-0,0095=-0,0238 рад;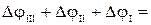 - 0,0233+0,009-0,0095-0,0218=-0,0456рад.
- 0,0233+0,009-0,0095-0,0218=-0,0456рад.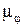 =
= 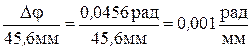 .
. и полный угол закручивания -0,0456 рад.
и полный угол закручивания -0,0456 рад.


 .
. =490/1,2=408 Мпа.
=490/1,2=408 Мпа. .
. *100%=
*100%=  = 81,7%, что выше допустимого (10%).
= 81,7%, что выше допустимого (10%).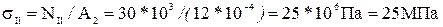 .
. =113/1,2=94,2 Мпа.
=113/1,2=94,2 Мпа. .
. *100%=
*100%=  = 73,4%, что выше допустимого (10%).
= 73,4%, что выше допустимого (10%). .
. .
. =11,6 %, что выше допустимого (10%).
=11,6 %, что выше допустимого (10%). =
=  .
.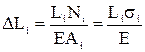 ,
, – соответственно длина участка, внутреннее усилие, площадь поперечного сечения, напряжение в сечении. Е –модуль упругости материала.
– соответственно длина участка, внутреннее усилие, площадь поперечного сечения, напряжение в сечении. Е –модуль упругости материала. .
.
 .
. =27,78*10-5м;
=27,78*10-5м; =31,95*10-5м;
=31,95*10-5м;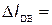 31,95*10-5м
31,95*10-5м 27,78*10-5 +4,17*10-5-31,25*10-5=0,7*10-5м.
27,78*10-5 +4,17*10-5-31,25*10-5=0,7*10-5м.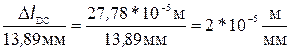 .
.