
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Третья гипотеза прочности – наибольших касательных напряженийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Согласно третьей гипотезе прочности наибольших касательных напряжений, причиной разрушения материала являются наибольшие Касательные напряжения. Максимальное касательное напряжение для заданного объемного напряженного состояния и эквивалентного ему линейного напряженного состояния одинаковы: Формула наибольшего касательного напряжения при объемном напряженном состоянии: Условие прочности по третьей гипотезе прочности:
Третья гипотеза прочности не учитывает второго главного напряжения ( ЧЕТВЕРТАЯ ГИПОТЕЗА ПРОЧНОСТИ - ЭНЕРГЕТИЧЕСКАЯ Четвертая (энергетическая) гипотеза прочности: количество удельной потенциальной энергии изменения формы, накопленной к моменту наступления предельного состояния материала, одинаково как при сложном напряженном состоянии, так и при простом одноосном растяжении. В четвертой гипотезе прочности речь идет не обо всей удельной потенциальной энергии деформации, а лишь ее части, которая накапливается за счет изменения формы кубика с ребром равным единице. В общем случае полная удельная потенциальная энергия деформации может быть представлена как сумма энергий, связанных с изменением объема кубика и изменением его формы. Условие прочности по четвертой гипотезе прочности:
Достоинство четвертой гипотезы прочности: эквивалентное напряжение определяется значениями всех трех главных напряжений. Энергетическая гипотеза прочности согласуется с опытными данными для пластичных материалов. ГИПОТЕЗА ПРОЧНОСТИ МОРА Согласно гипотезе прочности Мора, предложенной Отто Мором, два напряженных состояния равноопасны, если для соответствующих главных напряжений Условие прочности по гипотезе прочности Мора: Гипотеза прочности Мора не учитывает влияния второго главного напряжения ( Коэффициент Гипотеза прочности Мора рекомендуется для хрупких материалов. Для пластичных материалов гипотеза прочности Мора тождественна третьей гипотезе прочности.
Критическая сила для сжатие стержней Критическая сила
Проинтегрировав это выражение и учитывая при этом граничные условия, Л. Эйлером получено уравнение для определения критической силы:
где
При изменении условий закрепления стержня величина критической силы изменяется. На схеме (рис. 2.24, г) изображен стержень длиной
где (
Рис. 2.25. Способы закрепления стержня
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 958; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 .
. . Эквивалентное напряжение при одноосном растяжении:
. Эквивалентное напряжение при одноосном растяжении:  .
.
 ). Однако, опыты показывают, что для пластичных материалов гипотеза наибольших касательных напряжений дает удовлетворительные результаты. Ошибка от пренебрежения влиянием
). Однако, опыты показывают, что для пластичных материалов гипотеза наибольших касательных напряжений дает удовлетворительные результаты. Ошибка от пренебрежения влиянием 
 и
и 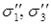 соблюдается соотношение:
соблюдается соотношение:  .
.
 представляет собой отношение предельных напряжений, соответствующих одноосным растяжению и сжатию, который равен для хрупких материалов:
представляет собой отношение предельных напряжений, соответствующих одноосным растяжению и сжатию, который равен для хрупких материалов: 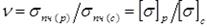 , для пластичных:
, для пластичных:  .
. .Пусть при достижении силы критического значения
.Пусть при достижении силы критического значения  стержень сохраняет изогнутую форму и находится в равновесии (рис.2.24, б). В сечении, отстоящем на расстоянии
стержень сохраняет изогнутую форму и находится в равновесии (рис.2.24, б). В сечении, отстоящем на расстоянии 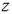 от начала координат, действует изгибающий момент
от начала координат, действует изгибающий момент  .
Если предположить, что потеря устойчивости происходит при напряжениях, не превышающих предела пропорциональности
.
Если предположить, что потеря устойчивости происходит при напряжениях, не превышающих предела пропорциональности  , и что имеют место лишь малые отклонения от прямолинейной формы, то дифференциальное уравнение изогнутой оси стержня принимает вид (см. п. 2.5.5):
, и что имеют место лишь малые отклонения от прямолинейной формы, то дифференциальное уравнение изогнутой оси стержня принимает вид (см. п. 2.5.5):
 .
При потере устойчивости стержень изгибается в плоскости наименьшей жесткости, т.е. поперечные
сечения стержня будут поворачиваться вокруг той оси, относительно которой момент инерции имеет минимальное значение. Поэтому следует считать
.
При потере устойчивости стержень изгибается в плоскости наименьшей жесткости, т.е. поперечные
сечения стержня будут поворачиваться вокруг той оси, относительно которой момент инерции имеет минимальное значение. Поэтому следует считать  .
Поскольку прогиб
.
Поскольку прогиб  и вторая производная от него
и вторая производная от него  всегда имеют разные знаки, то
всегда имеют разные знаки, то  и
и 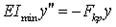 .
.
 Рис. 2.24. Устойчивость сжатых стержней
Рис. 2.24. Устойчивость сжатых стержней
 ,
,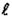 – длина стержня;
– длина стержня;  – любое целое число (n =1; 2; 3 и т.д.). При n =1 (рис. 2.24, в) стержень изгибается по одной полуволне синусоиды (устойчивое равновесие), а при всех последующих значениях n число полуволн равно номеру соответствующей критической силы (равновесие неустойчивое). Для практических расчетов интерес представляет наименьшая критическая сила:
– любое целое число (n =1; 2; 3 и т.д.). При n =1 (рис. 2.24, в) стержень изгибается по одной полуволне синусоиды (устойчивое равновесие), а при всех последующих значениях n число полуволн равно номеру соответствующей критической силы (равновесие неустойчивое). Для практических расчетов интерес представляет наименьшая критическая сила: . (2.71)
. (2.71) вместо
вместо  , (2.72)
, (2.72) ) – приведенная длина стержня;
) – приведенная длина стержня; 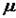 – коэффициент приведения, показывающий, во сколько раз следует изменить длину шарнирно-закрепленного стержня, чтобы значение критической силы для него было бы равно критической силе
– коэффициент приведения, показывающий, во сколько раз следует изменить длину шарнирно-закрепленного стержня, чтобы значение критической силы для него было бы равно критической силе 



