
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вращательное движение твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Вращательным называют такое движение твердого тела, при котором две какие-нибудь точки принадлежащие телу, остаются во все время движения неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все точки лежащие на оси так же неподвижны. Чтобы определить положение вращающегося тела, введем две плоскости, проходящие через ось вращения (рис. 50 Теперь в любой момент времени положение тела будет определяться углом
Угол поворота обычно измеряют в радианах. Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость Если за промежуток времени
Угловой скоростью тела в данный момент t называется величина, к которой стремится средняя угловая скорость
Угловая скорость твердого тела является первой производной от угла поворота по времени. Размерность: [радиан/время]; [1/время]; [1/сек = Угловую скорость можно изображать вектором. Вектор угловой скорости Если угловая скорость не является постоянной величиной, то вводят еще одну характеристику вращения - угловое ускорение. Угловое ускорение характеризует изменение угловой скорости тела с течением времени. Если за промежуток времени
Угловая скорость.19Угловое ускорение Угловая скорость
Углова́я ско́рость — векторная величина, являющаяся 0%90%D0%BA%D1%81%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80"псевдовектором (аксиальным вектором) и характеризующая скорость 0%92%D1%80%D0%B0%D1%89%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D0%B4%D0%B2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5"вращения 0%9C%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%82%D0%BE%D1%87%D0%BA%D0%B0"материальной точки вокруг центра вращения. Вектор угловой скорости по величине равен 0%A3%D0%B3%D0%BE%D0%BB"углу поворота точки вокруг центра вращения в единицу времени:
Углово́е ускоре́ние — 0%9F%D1%81%D0%B5%D0%B2%D0%B4%D0%BE%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80"псевдовекторная 0%A4%D0%B8%D0%B7%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%B2%D0%B5%D0%BB%D0%B8%D1%87%D0%B8%D0%BD%D0%B0"физическая величина, характеризующая быстроту изменения 0%A3%D0%B3%D0%BB%D0%BE%D0%B2%D0%B0%D1%8F_%D1%81%D0%BA%D0%BE%D1%80%D0%BE%D1%81%D1%82%D1%8C"угловой скорости 0%9C%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%82%D0%BE%D1%87%D0%BA%D0%B0"материальной точки. При 0%92%D1%80%D0%B0%D1%89%D0%B5%D0%BD%D0%B8%D0%B5"вращении точки вокруг неподвижной 0%9E%D1%81%D1%8C_%D0%B2%D1%80%D0%B0%D1%89%D0%B5%D0%BD%D0%B8%D1%8F"оси, угловое ускорение по модулю равно0%A3%D0%B3%D0%BB%D0%BE%D0%B2%D0%BE%D0%B5_%D1%83%D1%81%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D0%B8%D0%B5"[1]:
Вектор углового ускорения При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости
и направлен по касательной к 0%93%D0%BE%D0%B4%D0%BE%D0%B3%D1%80%D0%B0%D1%84"годографу вектора Существует связь между 0%A2%D0%B0%D0%BD%D0%B3%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%83%D1%81%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D0%B8%D0%B5"тангенциальным и угловым ускорениями:
где R — 0%A0%D0%B0%D0%B4%D0%B8%D1%83%D1%81_%D0%BA%D1%80%D0%B8%D0%B2%D0%B8%D0%B7%D0%BD%D1%8B"радиус кривизны 0%A2%D1%80%D0%B0%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%B8%D1%8F_%D0%BC%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B9_%D1%82%D0%BE%D1%87%D0%BA%D0%B8"траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/с².
|
|||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 ) А - плоскость неподвижная; В - плоскость связанная с телом и вращающаяся с ним; DE - ось вращения, совпадающая с осью z.
) А - плоскость неподвижная; В - плоскость связанная с телом и вращающаяся с ним; DE - ось вращения, совпадающая с осью z. между плоскостями А и В или углом поворота тела, положительным, если вращение происходит против часовой стрелки, и отрицательным в противном случае. Закон вращательного движения
между плоскостями А и В или углом поворота тела, положительным, если вращение происходит против часовой стрелки, и отрицательным в противном случае. Закон вращательного движения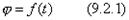
 и угловое ускорение
и угловое ускорение  .
.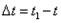 тело совершает поворот на угол
тело совершает поворот на угол  , то средняя угловая скорость будет численно равна
, то средняя угловая скорость будет численно равна
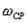 , если
, если  стремится к нулю.
стремится к нулю.
 ].
]. направляют по оси вращения в ту сторону, откуда вращение видно против хода часовой стрелки.
направляют по оси вращения в ту сторону, откуда вращение видно против хода часовой стрелки. , то среднее угловое ускорение равно
, то среднее угловое ускорение равно
 Быстрота изменения угла φ – это угловая скорость:
ω=dφ/dt=φ', рад/с; с-1. (2.3)
Приняв k как единичный орт положительного направления оси, получим
Быстрота изменения угла φ – это угловая скорость:
ω=dφ/dt=φ', рад/с; с-1. (2.3)
Приняв k как единичный орт положительного направления оси, получим
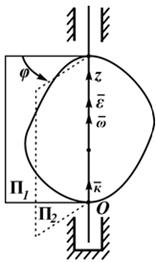
 Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Изменение угловой скорости характеризуется угловым ускорением:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Изменение угловой скорости характеризуется угловым ускорением:
 Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном - противоположны.
Для некоторых частных случаев вращательного движения могут быть использованы формулы:
- равномерное вращение (ω - const)
φ=φ0+ωt; (2.5)
- равнопеременное вращение (ε - const)
ω=ω0+εt; φ=φ0+ω0t+εt2/2. (2.6)
В технике угловая скорость часто задается в оборотах в минуту n[об/мин]. Один оборот – это 2π радиан:
ω=n⋅2π/60=nπ/30 рад/с; с-1.
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном - противоположны.
Для некоторых частных случаев вращательного движения могут быть использованы формулы:
- равномерное вращение (ω - const)
φ=φ0+ωt; (2.5)
- равнопеременное вращение (ε - const)
ω=ω0+εt; φ=φ0+ω0t+εt2/2. (2.6)
В технике угловая скорость часто задается в оборотах в минуту n[об/мин]. Один оборот – это 2π радиан:
ω=n⋅2π/60=nπ/30 рад/с; с-1.
 ,
,
 направлен вдоль оси вращения (в сторону
направлен вдоль оси вращения (в сторону  при ускоренном вращении и противоположно
при ускоренном вращении и противоположно  по времени0%A3%D0%B3%D0%BB%D0%BE%D0%B2%D0%BE%D0%B5_%D1%83%D1%81%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D0%B8%D0%B5"[2], то есть
по времени0%A3%D0%B3%D0%BB%D0%BE%D0%B2%D0%BE%D0%B5_%D1%83%D1%81%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D0%B8%D0%B5"[2], то есть ,
, ,
,


