
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание движений твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Следующей по сложности моделью после частицы является абсолютно твердое тело - в нем расстояние между любыми двумя точками не меняется в процессе движения. Описание движения твердого тела кроме самостоятельного значения имеет большое значение и в применении к описаниям других видов движения. Система отсчета, служащая для пространственно-временного описания различных движений может быть связана только с твердым телом. Поэтому изучение движения твердых тел равносильно изучению движений систем отсчета. Результаты этого раздела будут неоднократно использоваться в дальнейшем. Имеется пять видов движения твердого тела: 1) поступательное, если прямая, соединяющая любые две точки тела, перемещается, оставаясь параллельной своему начальному положению, например движение трамвая на прямом участке пути; 2) вращательно е, если все точки лежащие на некоторой прямой, называемой осью вращения, остаются неподвижными, например движение двери при открывании и закрывании; 3) плоское, если все точки тела движутся в плоскостях, параллельных некоторой плоскости, неподвижной в рассматриваемой системе отсчета, например качение колеса на прямом участке пути; 4) сферическое, если одна из точек тела остается все время неподвижной в рассматриваемой системе отсчета, например движение гироскопа с тремя степенями свободы в карданном подвесе; 5) свободное, если нет перечисленных выше четырех ограничений, например движение свободного произвольного брошенного тела вблизи поверхности Земли. Первые два движения являются основными движениями твердого тела. Остальные виды движения твердого тела можно свести к одному из основных движений или к их совокупности (это будет показано на примере плоского движения). В этом разделе рассмотрим первые три вида движения и вопрос сложения угловых скоростей. При поступательном движении все точки твердого тела совершают равные перемещения за один и тот же промежуток времени. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Этот факт позволяет свести изучение поступательного движения твердого тела к изучению движения отдельной частицы тела, т. е. к задаче кинематики частицы. Таким образом, поступательное движение твердого тела может быть полностью описано, если известны зависимость от времени радиус-вектора 2.3 Плоскопараллельное движение твердого тела Плоскопараллельным (плоским) движением (ППД) твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости (рисунок 2.11).
При таком движении точки, лежащие в разных плоскостях на одном отрезке, перпендикулярном неподвижной плоскости (например M1M2) совершают одинаковые движения.
Рисунок 2.11
Рисунок 2.12
Отрезок M1M2 движется поступательно. Поэтому изучение плоскопараллельного движения сводится к изучению движения плоской фигуры в какой-то плоскости. На рисунке 2.12 показано перемещение пластинки в плоской системе отсчета xOy из одного положения в другое. Такое перемещение можно осуществить двигая пластину поступательно с траекторией точки A с последующим поворотом на угол φ вокруг точки A1. Это же перемещение можно выполнить иначе.
Например, перемещая пластинку поступательно с траекторией точки B, с последующим поворотом вокруг B1 на угол φ. Траектории точек A и B различны, а угол поворота в обоих случаях одинаков.
Положение пластинки вполне определяется положением скрепленного с ней отрезка (например AB), закон движения которого можно задать в виде: xA=xA(t), yA=yA(t), φ=φ(t). Точка A в этом случае называется полюсом. Если принять за полюс точку B, то получим уравнения: x B =xB(t), yB=yB(t), φ=φ(t)
За полюс выбирается точка, закон движения которой известен. Мгновенный центр скоростей
Аксиомы динамики Первая аксиома динамики. Существуют системы отсчета, в которых материальная точка покоится, либо движется прямолинейно и равномерно, если она не подвергается воздействиям. Такие системы отсчета называют инерциальными. Инерциальные системы отсчета эквивалентны в том смысле, что в них одинаково соблюдаются все законы механики. Воздействие на материальную точку со стороны какого-либо объекта характеризуется силой. Вторая аксиома динамики. Если в инерциальной системе отсчета материальная точка движется с ускорением (рис. 1), то на нее действует сила, пропорциональная ускорению. Коэффициентом пропорциональности является масса точки. Третья аксиома динамики. Силовое воздействие всегда сопровождается таким же по величине силовым противодействием. Из третьей аксиомы следует, что материальная точка всегда противодействует ускоряющему ее объекту. Согласно второй аксиоме, сила такого противодействия. Методы кинематики Кинема́тика (0%93%D1%80%D0%B5%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D1%8F%D0%B7%D1%8B%D0%BA"греч. κινειν — двигаться) в физике — раздел 0%9C%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0"механики, изучающий математическое описание (средствами 0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F"геометрии, 0%90%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0"алгебры, 0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7"математического анализа…) движения идеализированных тел (0%9C%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%82%D0%BE%D1%87%D0%BA%D0%B0"материальная точка, 0%90%D0%B1%D1%81%D0%BE%D0%BB%D1%8E%D1%82%D0%BD%D0%BE_%D1%82%D0%B2%D0%B5%D1%80%D0%B4%D0%BE%D0%B5_%D1%82%D0%B5%D0%BB%D0%BE"абсолютно твердое тело, 0%98%D0%B4%D0%B5%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D0%B6%D0%B8%D0%B4%D0%BA%D0%BE%D1%81%D1%82%D1%8C"идеальная HYPERLINK "http://ru.wikipedia.org/wiki/%D0%98%D0%B4%D0%B5%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D0%B6%D0%B8%D0%B4%D0%BA%D0%BE%D1%81%D1%82%D1%8C"жидкость), без рассмотрения причин движения (0%9C%D0%B0%D1%81%D1%81%D0%B0"массы, 0%A1%D0%B8%D0%BB%D0%B0"сил и т. д.). Исходные понятия кинематики — 0%9F%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE_%D0%B2_%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B5"пространство и 0%92%D1%80%D0%B5%D0%BC%D1%8F"время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования 0%A6%D0%B5%D0%BD%D1%82%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B5%D0%BC%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%83%D1%81%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D0%B8%D0%B5"центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения 0%9C%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D0%B4%D0%B2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5"механического движения занимается другой раздел механики — 0%94%D0%B8%D0%BD%D0%B0%D0%BC%D0%B8%D0%BA%D0%B0_(%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0)"динамика.
|
|||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 542; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

 любой точки этого тела и его положение в начальный момент, как это было описано в предыдущем разделе
любой точки этого тела и его положение в начальный момент, как это было описано в предыдущем разделе

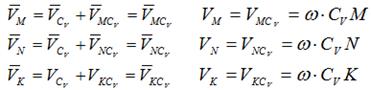 Из рис. 1.5 видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение
Из рис. 1.5 видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение

 Рис. 1.5
На нижеприведенных рисунках показаны примеры определения положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.
Рис. 1.5
На нижеприведенных рисунках показаны примеры определения положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.
 Для рисунка 1.6:
1. СV совпадает с точкой В VB=0. Шатун АВ вращается вокруг точки В
Для рисунка 1.6:
1. СV совпадает с точкой В VB=0. Шатун АВ вращается вокруг точки В
 2.
2.
 3. МЦС лежит в «бесконечности»
3. МЦС лежит в «бесконечности»

 22. Теорема сложение скоростей
22. Теорема сложение скоростей




