Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полярный момент инерции. Полярный момент инерции для круга, для кольца.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Полярный момент инерции [0%9F%D0%BE%D0%BB%D1%8F%D1%80%D0%BD%D1%8B%D0%B9_%D0%BC%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D0%B8%D0%BD%D0%B5%D1%80%D1%86%D0%B8%D0%B8&veaction=edit&vesection=0"править | 0%9F%D0%BE%D0%BB%D1%8F%D1%80%D0%BD%D1%8B%D0%B9_%D0%BC%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D0%B8%D0%BD%D0%B5%D1%80%D1%86%D0%B8%D0%B8&action=edit§ion=0"править исходный текст] Материал из Википедии — свободной энциклопедии Не следует путать с 0%9C%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D0%B8%D0%BD%D0%B5%D1%80%D1%86%D0%B8%D0%B8"Момент инерции.
Схема к вычислению полярного момента инерции Поля́рный моме́нт ине́рции — интегральная сумма произведений площадей элементарных площадок dA на квадрат расстояния их от полюса — ρ2 (в 0%9F%D0%BE%D0%BB%D1%8F%D1%80%D0%BD%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%BA%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82"полярной системе координат), взятая по всей площади сечения. То есть:
Эта величина используется для прогнозирования способности объекта оказывать сопротивление 0%9A%D1%80%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D0%B5"кручению. Она имеет размерность единиц длины в четвёртой степени (м4, см4) и может быть лишь положительной. Для площади сечения, имеющей форму 0%9A%D1%80%D1%83%D0%B3"круга 0%A0%D0%B0%D0%B4%D0%B8%D1%83%D1%81"радиусом r полярный момент инерции равен:
Если совместить начало 0%94%D0%B5%D0%BA%D0%B0%D1%80%D1%82%D0%BE%D0%B2%D0%B0_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%BA%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82"декартовой прямоугольной системы координат 0 с полюсом полярной системы (см. рис.), то
потому что Полярный момент - инерция - круг Страница 1
Полярный момент инерции круга в два раза больше осевого момента инерции круга относительно оси, проходящей через его центр. [ 1 ] Вычислим полярный момент инерции круга относительно его центра, а также момент инерции относительно центральной оси. [ 2 ] Определим полярный момент инерции круга относительно его центра. [ 3 ] Зная полярный момент инерции круга относительно центра, легко найти его момент инерции относительно диаметра. Поскольку осевые моменты инерции одинаковы для всех диаметров, из (А. [ 4 ] Вычислим полярный момент инерции круга относительно его центра, а также момент инерции относительно центральной оси. [ 5 ] Чему равны полярные моменты инерции круга и кольца относительно их центров. [ 6 ] Сначала определяем полярный момент инерции круга. [ 7 ] Установим формулу для определения полярного момента инерции круга. [ 8 ] Рассмотрим теперь, как вычисляется полярный момент инерции круга относительно его центра (рис. А. [ 9 ] Исходя из этого определения, вычислим полярный момент инерции круга. [ 10 ] В предыдущей главе без вывода были приведены формулы для полярных моментов инерции круга и кругового кольца; выведем эти формулы. [ 11 ] Чему равны осевые моменты инерции круга и кольца относительно осей, проходящих через их центры тяжести. Чему равны полярные моменты инерции круга и кольца относительно их центров. [ 12 ] Изгиб. Основные понятия Изгиб — вид деформации, при котором происходит искривление осей прямых 0%91%D1%80%D1%83%D1%81_(%D0%BC%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0)"брусьев или изменение 0%9A%D1%80%D0%B8%D0%B2%D0%B8%D0%B7%D0%BD%D0%B0"кривизны осей кривых брусьев. Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов. Прямой изгиб возникает в случае, когда 0%98%D0%B7%D0%B3%D0%B8%D0%B1%D0%B0%D1%8E%D1%89%D0%B8%D0%B9_%D0%BC%D0%BE%D0%BC%D0%B5%D0%BD%D1%82"изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, называется косым. Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечении действует также и поперечная сила, то имеется поперечный прямой или поперечный косой изгиб. Часто термин «прямой» в названии прямого чистого и прямого поперечного изгиба не употребляют и их называют соответственно чистым изгибом и поперечным изгибом. Лекция 6. Плоский изгиб Изгибом называется вид нагружения бруса, при котором к нему прикладывается момент, лежащий в плоскости проходящей через продольную ось. В поперечных сечениях бруса возникают изгибающие моменты. При изгибе возникают деформация, при которой происходит искривление оси прямого бруса или изменение кривизны кривого бруса. Брус, работающий при изгибе, называется балкой. Конструкция, состоящая из нескольких изгибаемых стержней, соединенных между собой чаще всего под углом 90°, =07K205BAO рамой. Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.6.1).
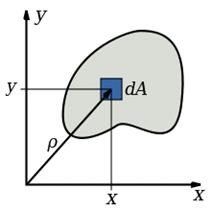
Рис.6.1
При плоском поперечном изгибе в балке возникают два вида внутренних усилий: поперечная сила Q и изгибающий момент M. В раме при плоском поперечном изгибе возникают три усилия: продольная N, поперечная Q силы и изгибающий момент M. Если изгибающий момент Косой изгиб - изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции. Сложный изгиб - изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях. Далее будем рассматривать плоский изгиб, то есть все силы будем прилагать в плоскости симметрии балки.
Рис.6.2
Осваивать расчет балок и рам удобно, рассматривая по очереди следующие вопросы: - Определение внутренних усилий в балках и построение эпюр внутренних усилий. - Проверка прочности балок. - Определение перемещений и проверка жесткости балок. Решение этих вопросов получим в соответствующих разделах на примере конкретных задач.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


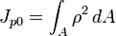
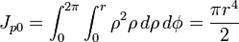
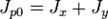
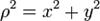 .
.
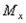 является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.6.2). При наличии поперечной силы
является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.6.2). При наличии поперечной силы  изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.
изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.