
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет момента инерции маятникаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пока сила тяжести Р, приложенная в центре масс С, направлена вдоль оси стержня (рис. 5.1, а), система находится в равновесии. Если отклонить стержень на некоторый малый угол
где Вращающий момент М, создаваемый силой Р, при малых углах
Он вызывает ускорение при вращательном движении маятника. Связь между этим ускорением и моментом сил дается основным уравнением динамики вращательного движения
где J – момент инерции маятника относительно оси О. Обозначим
Тогда из уравнения (5.2) получим
Уравнение (5.4) описывает колебательный процесс с циклической частотой
Период колебаний, следовательно, равен
Из формулы (5.5) выразим момент инерции
Если положение центра масс системы не изменяется, то величина L постоянна и в формулу (5.6) можно ввести постоянный коэффициент
Измеряя время t, в течение которого происходит n полных колебаний, найдем период
С помощью формулы (5.8) производятся косвенные измерения момента инерции физического маятника относительно оси О. С другой стороны, момент инерции J зависит от положения грузов
где Преобразуя формулу (5.9), получаем
где Зависимость (5.10) будем проверять, получая величины J и JA экспериментально с помощью формулы (5.8).
Задание к работе
1. При подготовке к лабораторной работе получите расчетную формулу для погрешности косвенных измерений D J момента инерции (см. Введение). Учтите, что момент инерции определяется с помощью рабочей формулы (5.8). Для упрощения вычислений можно считать, что коэффициент K в этой формуле измерен точно: D K = 0. 2. Подготовьте эскиз табл. 1 для статистической обработки прямых пятикратных измерений времени t (образец см. Введение табл. В.1). 3. Подготовьте эскиз табл. 2 для исследования зависимости J от x 2. 4. Включите электронный секундомер. Нажатием кнопки «Режим» установите режим №3 (светится индикатор «Реж.3»), при этом отключится тормозное устройство, удерживающее тело. 5. Приступая к работе, поместите оба груза 6. Отклоните маятник рукой на небольшой угол 7. Проведите пятикратные измерения времени t десяти полных колебаний физического маятника, не меняя положение грузов. 8. Рассчитайте среднее время 9. Используя рабочую формулу (5.8), определите значение момента инерции JA, а по формуле, полученной в п. 1 этого задания, определите погрешность измерения этой величины D J. Результат запишите в виде 10. Раздвиньте грузы 11. Повторите опыт п. 7 при пяти различных расстояниях x. 12. Определите момент инерции маятника с помощью формулы (5.8) при различных расстояниях x. Результаты занесите в табл. 2. 13. Постройте график зависимости момента инерции маятника
Контрольные вопросы
1. В чем состоит цель данной работы? 2. Что такое момент инерции тела? В чем его физический смысл? 3. Сформулируйте и примените к данной работе основной закон динамики вращательного движения. 4. Что такое центр масс системы? 5. Почему местоположение центра масс маятника не меняется при изменении положения грузов 6. Найдите момент инерции системы относительно центра масс, задав или измерив нужные для этого величины. 7. Сформулируйте закон сохранения энергии и запишите его применительно к физическому маятнику. 8. Как получить рабочую формулу (5.8) и зависимость (5.10)? 9. Как получить формулу для расчета погрешности косвенных измерений момента инерции? 10. Как формулируется теорема Штейнера? Как можно применить ее к исследуемой системе? 11. Почему предлагается построить график зависимости момента инерции от квадрата величины x? 12. Что такое момент силы
Индивидуальные задания для членов бригады, выполняющих лабораторную работу на одной установке
Литература
Савельев И.В. Курс общей физики. – М.: Наука, 1982. – Т. 1 (и последующие издания этого курса).
Лабораторная работа № 6
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ МЕТОДОМ КЛЕМАНА И ДЕЗОРМА
Цель работы – изучение равновесных термодинамических процессов и теплоемкости идеальных газов, измерение показателя адиабаты классическим методом Клемана и Дезорма.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.007 с.) |

 (рис. 5.1, б), то центр масс С поднимается на небольшую высоту и тело приобретает запас потенциальной энергии. На маятник относительно оси О, направление которой выбираем «к нам», будет при этом действовать момент силы тяжести, проекция которого на эту ось равна
(рис. 5.1, б), то центр масс С поднимается на небольшую высоту и тело приобретает запас потенциальной энергии. На маятник относительно оси О, направление которой выбираем «к нам», будет при этом действовать момент силы тяжести, проекция которого на эту ось равна , (5.1)
, (5.1) ; L – расстояние между осью вращения О и центром масс С.
; L – расстояние между осью вращения О и центром масс С. .
. , (5.2)
, (5.2)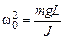 . (5.3)
. (5.3) . (5.4)
. (5.4) .
. . (5.5)
. (5.5) . (5.6)
. (5.6) . (5.7)
. (5.7) . Подставляя T и K в (5.6), получаем рабочую формулу
. Подставляя T и K в (5.6), получаем рабочую формулу . (5.8)
. (5.8) на стержне. Переместим грузы
на стержне. Переместим грузы  и
и  (см. рис. 5.1). Тогда их можно рассматривать как материальные точки. В этом случае момент инерции системы определяется выражением
(см. рис. 5.1). Тогда их можно рассматривать как материальные точки. В этом случае момент инерции системы определяется выражением , (5.9)
, (5.9) – момент инерции системы без грузов; x – расстояние груза
– момент инерции системы без грузов; x – расстояние груза  , (5.10)
, (5.10) – момент инерции маятника при положении грузов
– момент инерции маятника при положении грузов  и определите доверительную погрешность измерения D t.
и определите доверительную погрешность измерения D t. и занесите в табл. 2 для значения
и занесите в табл. 2 для значения  .
. (см. рис. 5.1). Рекомендуется расстояние
(см. рис. 5.1). Рекомендуется расстояние  , угловая скорость
, угловая скорость  , угловое ускорение
, угловое ускорение  , угловое перемещение
, угловое перемещение  , как направлены эти векторы?
, как направлены эти векторы?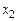 от точки А
от точки А



