
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пружинный, физический и математический маятникиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида (5.6):
Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются пружинный, физический и математический маятники. Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F=-kx, где k -коэффициент упругости, в случае пружины называемый жесткостью. Уравнение движения маятника
или
Из выражений (5.12) и (5.1) следует, что пружинный маятник совершает гармонические колебания по закону
и периодом
Формула (5.14) справедлива для упругих колебаний в пределах, в которых выполняется закон Гука, т.е. когда масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, согласно (5.10) и (5.13), равна
(4.5) момент М вращающей силы можно записать в виде
где J – момент инерции маятника относительно оси, проходящей через точку О, Уравнение (5.15) можно записать в виде
или
Принимая
получим уравнение
Из выражения (5.17) следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой w0 (см. (5.18)) и периодом
где Математический маятник – это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити.
Момент инерции математического маятника
где Так как математический маятник можно представить как частный случай физического маятника, предположив, что вся его масса сосредоточена в одной точке – центре его масс, то, подставив выражение (5.19) в формулу (5.18), получим выражение для периода малых колебаний математического маятника
Сравнивая формулы (5.18) и (5.20), видим, что если приведенная длина L физического маятника равна длине
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 802; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.140.54 (0.01 с.) |

 . (5.12)
. (5.12)
 .
.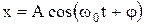 с циклической частотой
с циклической частотой (5.13)
(5.13) . (5.14)
. (5.14) .
.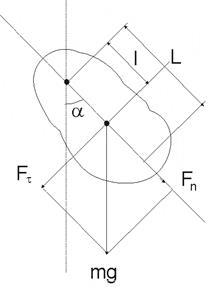 Рис. 28
Рис. 28
 , (5.15)
, (5.15) – расстояние между точкой подвеса и центром масс маятника,
– расстояние между точкой подвеса и центром масс маятника,  - возвращающая сила (знак минус обусловлен тем, что направление
- возвращающая сила (знак минус обусловлен тем, что направление 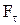 и a всегда противоположны; sina»a соответствует малым отклонениям маятника из положения равновесия).
и a всегда противоположны; sina»a соответствует малым отклонениям маятника из положения равновесия).
 .
. , (5.16)
, (5.16)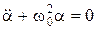 , идентичное (5.12), решение которого (5.1) известно:
, идентичное (5.12), решение которого (5.1) известно: . (5.17)
. (5.17) , (5.18)
, (5.18)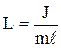 – приведенная длина физического маятника.
– приведенная длина физического маятника. , (5.19)
, (5.19)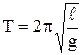 . (5.20)
. (5.20)


