
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение колебаний связанных маятниковСодержание книги
Поиск на нашем сайте
Лабораторная работа № 22 ИЗУЧЕНИЕ КОЛЕБАНИЙ СВЯЗАННЫХ МАЯТНИКОВ Цель работы: Исследование колебаний системы двух связанных маятников. Измерение собственных частот колебаний и частоты биений, экспериментальная проверка соотношения между этими частотами. Исследование зависимости частоты биений от параметров, определяющих связь маятников в системе. Оборудование: Два физических маятника, соединенные пружиной и оснащенные датчиками угла поворота, источник питания, электронный блок управления Cobra 3, компьютер.
Продолжительность работы – 4 часа.
Теоретическая часть
Биения Гармоническими колебаниями называются колебания, которые описываются формулой
где
в чем нетрудно убедиться, вычислив вторую производную от функции Некоторые физические задачи сводятся к сложению колебаний. Если суммируются колебания с одинаковыми частотами, то результирующие колебания происходят с той же частотой, а их амплитуда и начальная фаза могут быть найдены, например, с помощью метода векторных диаграмм. При сложении колебаний с разными частотами возникает сложный, в общем случае, непериодический процесс. Если частоты В качестве примера найдем сумму двух колебаний с одинаковыми амплитудами, начальными фазами, равными нулю, и близкими частотами:
Полученное выражение представим в виде
где Рис. 1. График биений, рассчитанный по формуле (3) при Определяя частоту биений формулой
где Описание установки Установка содержит два маятника, соединенные легкой пружиной (рис. 2б). На оси вращения каждого маятника закреплен датчик угла поворота, подключенный к блоку питания. Информационный сигнал с выхода датчика, пропорциональный углу отклонения маятника от положения равновесия, поступает на входы устройства преобразования «Cobra 3», и после преобразования в цифровую форму поступает в компьютер для обработки. Датчик угла поворота выполнен на основе резистивного моста (рис.3). Ползунок реостата связан со стержнем маятника. При повороте стержня изменяется соотношение сопротивлений резисторов и, следовательно, напряжение
Рис. 3. Схема резистивного датчика угла поворота.
Каждый из маятников представляет собой стержень, к которому прикреплен груз в виде диска. Масса груза
Экспериментальная часть. Подготовка к работе: 1. Установите заданное расстояние 2. Включите блок питания, компьютер и запустите программу «measure». Внимание! Перед включением приборов в сеть пригласите преподавателя или инженера для проверки схемы.
Подготовка к работе. 1. Физические понятия, знание которых необходимо для успешного выполнения работы: ü гармонические колебания; амплитуда, фаза, начальная фаза, период, частота, циклическая частота, дифференциальное уравнение гармонических колебаний; ü сложение гармонических колебаний, биения; ü математический и физический маятники, собственная частота колебаний; ü колебания связанной системы. 2. Приведите в конспекте подробный вывод формул (5) – (7) 3. Расчетное задание. ü По формулам (7), (8) рассчитайте зависимости
Примечание. Пункты 2, 3 выполните письменно при подготовке к лабораторной работе.
Литература 1. Иродов И.Е. Механика. Основные законы.– М.: Лаборатория базовых знаний, 2003, §§5.4, 6.1, 6.2, 6.3, 6.4. 2. Савельев И.В. Курс общей физики. Механика– М.: Астрель×АСТ, 2005; §§5.3, 5.4, 8.1, 8.5, 8.6, 8.7, 8.9, 8.11. 3. Фихтенгольц Г.М. Основы математического анализа. Т.2,Москва.: Лань, 2004; Глава 24,
Приложение-1 Вывод формул (5)-(9) При малых углах отклонения маятников от вертикали (
где
где
Рис. 1-1. Связанные маятники Полученные выражения для моментов сил подставим в уравнения динамики вращательного движения маятников:
где
где введены обозначения: Складывая уравнения системы (П1), получим
Вычитая из второго уравнения системы (П1) первое, получим
Из уравнений (П2), (П3) найдем
где
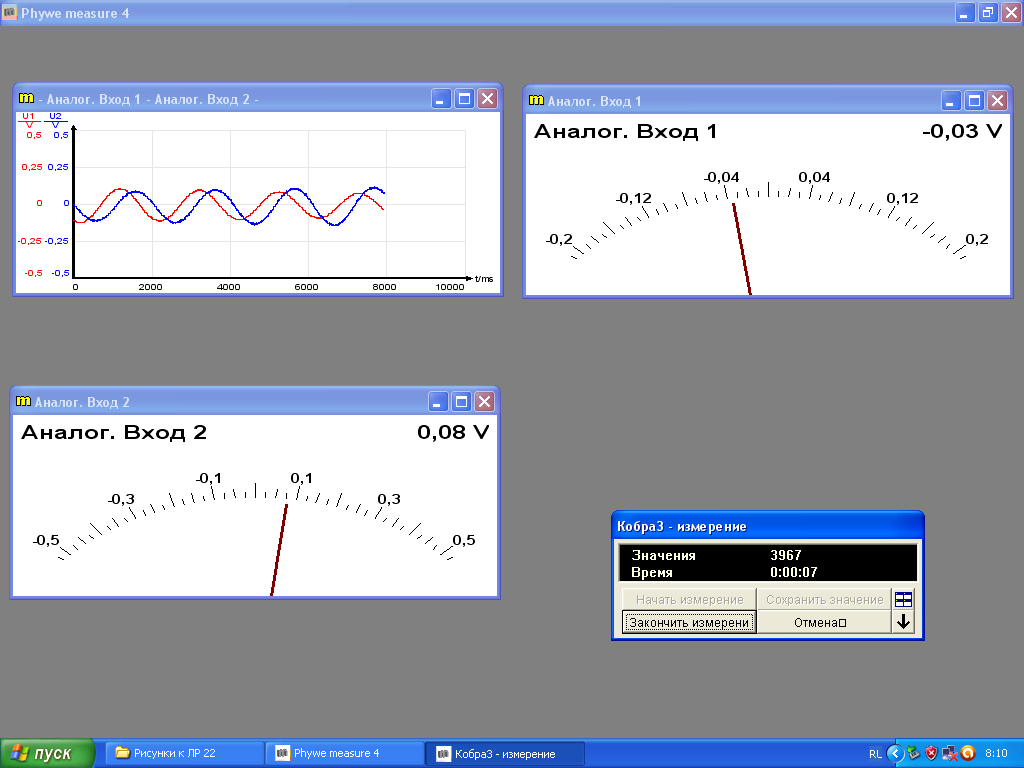
Приложение-2 Измерение собственных частот колебаний связанных маятников. 1. В меню «Прибор» компьютерной программы выберите «Универсальный измеритель». 2. В появившемся диалоговом окне наберите показанные на рис.2-1 установки. 3. Дважды отмечая мышкой окошки «Аналоговый дисплей» и «Диаграмма», активируйте на экране окна, изображенные на рис.2-2. Эти окна предназначены для установки максимального угла отклонения маятника от вертикали на аналоговом приборе и для выбора каналов, отображаемых на диаграмме.
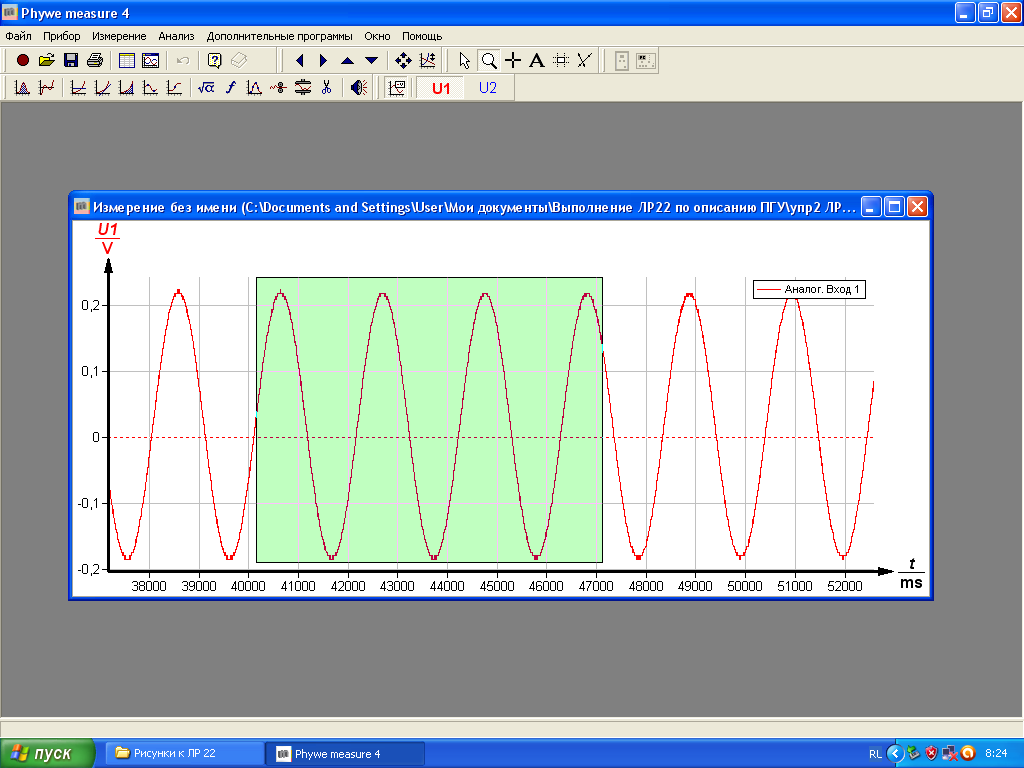
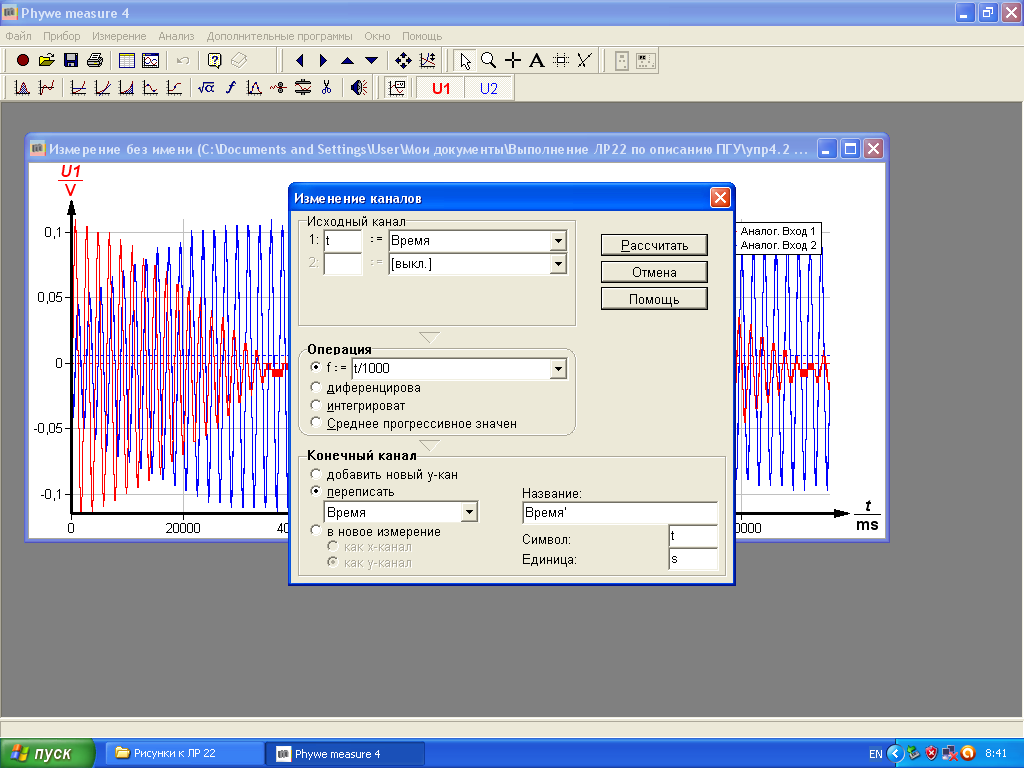
4. Конкретные значения параметров, устанавливаемых на рис.2-2, удобно выбрать, нажав кнопку «Далее» в окне на рис.2-1 и наблюдая отображение колебаний в появившемся на экране окне (рис.2-3). Предварительно нужно отклонить маятники на небольшие углы, отпустить их и нажать кнопку «Начать измерение» в правом нижнем углу окна на рис.2-3. Окончание процесса измерений выполняют нажатием клавиши «закончить измерение» в соответствующем окне на рис.2-3. 5. Когда маятники находятся в положении равновесия, приборы, изображенные на рис. 2-3, должны показывать нулевое напряжение - добейтесь этого с помощью ручек регулировки, расположенных на датчиках угла поворота. 6. Для измерения частот синфазных колебаний маятников отклоните их на одинаковые углы 7. Определите по графикам период синфазных колебаний 8. Аналогичным образом определите период 9. Рассчитайте собственные частоты (частоты синфазных и противофазных колебаний) и их погрешности: Приложение-3 Фурье-анализ биений 1. Выведите на экран график биений одного из маятников из упражнения 2. 2. Откройте окно «Изменение каналов», воспользовавшись инструментом «Формула» (На рис. 2-4 - 3. Заполните диалоговое окно так, как показано на рис.3-1. 4. Нажмите кнопку «Рассчитать», в результате на графике «биений» в 1000 раз уменьшится масштаб по оси времени (это необходимо, если учесть ожидаемые порядки собственных частот).
Рис.3-1. Окно для изменения масштаба по оси времени 5. Нажмите на панели инструментов кнопку f (Анализ Фурье). 6. В появившемся окне нажмите кнопку «Рассчитать». 7. Примените инструмент «Лупа» к графику на экране, «растянув» начальный участок этого графика. В результате получите зависимость как на рис.3-2.
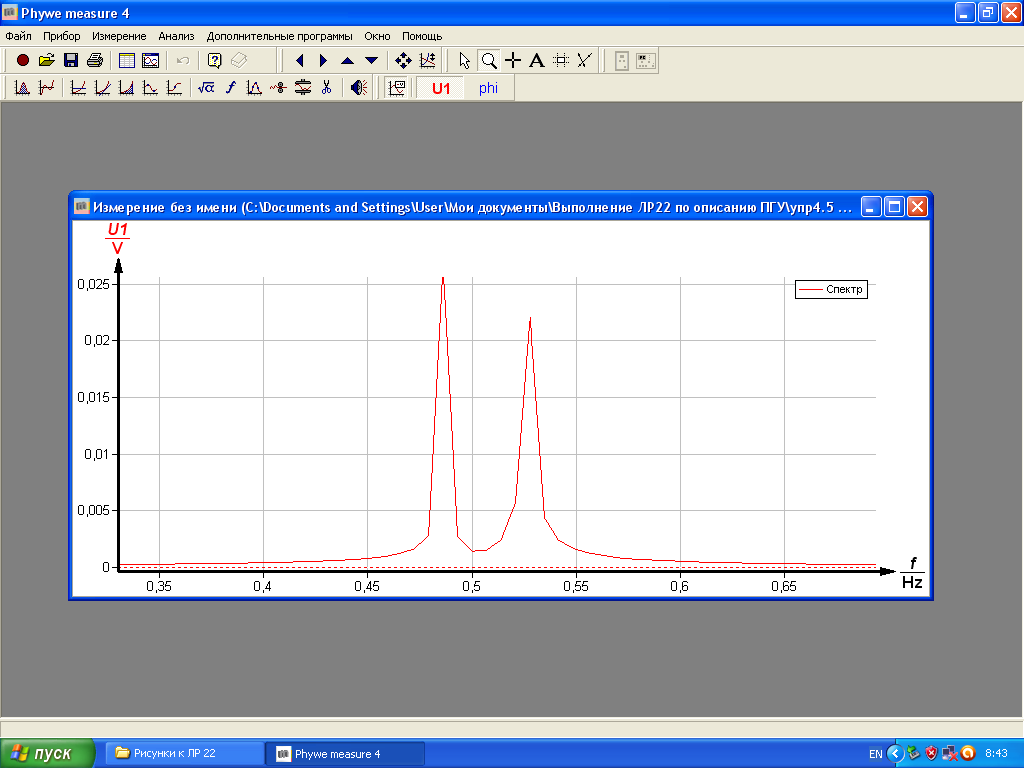
Рис.9. Пример Фурье – анализа спектра биений связанных маятников 8. С помощью инструмента «Обзор» определите абциссы пиков этого графика
Лабораторная работа № 22 ИЗУЧЕНИЕ КОЛЕБАНИЙ СВЯЗАННЫХ МАЯТНИКОВ Цель работы: Исследование колебаний системы двух связанных маятников. Измерение собственных частот колебаний и частоты биений, экспериментальная проверка соотношения между этими частотами. Исследование зависимости частоты биений от параметров, определяющих связь маятников в системе. Оборудование: Два физических маятника, соединенные пружиной и оснащенные датчиками угла поворота, источник питания, электронный блок управления Cobra 3, компьютер.
Продолжительность работы – 4 часа.
Теоретическая часть
Биения Гармоническими колебаниями называются колебания, которые описываются формулой
где
в чем нетрудно убедиться, вычислив вторую производную от функции Некоторые физические задачи сводятся к сложению колебаний. Если суммируются колебания с одинаковыми частотами, то результирующие колебания происходят с той же частотой, а их амплитуда и начальная фаза могут быть найдены, например, с помощью метода векторных диаграмм. При сложении колебаний с разными частотами возникает сложный, в общем случае, непериодический процесс. Если частоты В качестве примера найдем сумму двух колебаний с одинаковыми амплитудами, начальными фазами, равными нулю, и близкими частотами:
Полученное выражение представим в виде
где Рис. 1. График биений, рассчитанный по формуле (3) при Определяя частоту биений формулой
где
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 782; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.57.57 (0.01 с.) |

 , (1)
, (1) - координата колеблющейся точки,
- координата колеблющейся точки,  - амплитуда колебаний,
- амплитуда колебаний,  - циклическая частота,
- циклическая частота,  - период колебаний,
- период колебаний,  - начальная фаза. Гармонические колебания совершает, например, маятник при малых амплитудах. Формула (1) является решением дифференциального уравнения
- начальная фаза. Гармонические колебания совершает, например, маятник при малых амплитудах. Формула (1) является решением дифференциального уравнения , (2)
, (2) и подставив ее в дифференциальное уравнение (2). Амплитуда колебаний и начальная фаза определяются начальными условиями: координатой и скоростью материальной точки в начальный момент времени.
и подставив ее в дифференциальное уравнение (2). Амплитуда колебаний и начальная фаза определяются начальными условиями: координатой и скоростью материальной точки в начальный момент времени. и
и  складываемых колебаний близки по величине (
складываемых колебаний близки по величине ( , где
, где  ), то результирующие колебания имеют характер биений – так называют колебания с пульсирующей амплитудой (рис.1).
), то результирующие колебания имеют характер биений – так называют колебания с пульсирующей амплитудой (рис.1). . (3)
. (3) ,
, и
и  . Величину
. Величину  можно назвать медленно изменяющейся амплитудой. На рис. 1 приведен рассчитанный по формуле (3) график при
можно назвать медленно изменяющейся амплитудой. На рис. 1 приведен рассчитанный по формуле (3) график при  ,
,  10 с-1,
10 с-1,  с-1. Периодом биений
с-1. Периодом биений  называют минимальное время, за которое амплитуда колебаний периодически достигает своего минимального (или максимального) значения. Период изменения функции
называют минимальное время, за которое амплитуда колебаний периодически достигает своего минимального (или максимального) значения. Период изменения функции  равен
равен  , а период биений, как видно из рис. 1, в два раза меньше:
, а период биений, как видно из рис. 1, в два раза меньше:  .
. ,
,  ,
,  (сплошная кривая). Штриховая кривая рассчитана по формуле
(сплошная кривая). Штриховая кривая рассчитана по формуле 
 , получим
, получим , (4)
, (4) ,
,  .
. , измеряемое вольтметром. Это напряжение пропорционально углу
, измеряемое вольтметром. Это напряжение пропорционально углу  отклонения маятника. Ручная регулировка второго реостата (верхнего на рис.3) необходима для установки нулевого напряжения в положении равновесия маятника.
отклонения маятника. Ручная регулировка второго реостата (верхнего на рис.3) необходима для установки нулевого напряжения в положении равновесия маятника.


 кг, его диаметр d = 80 мм. Расстояние от центра масс маятника до точки подвеса может изменяться в небольших пределах (
кг, его диаметр d = 80 мм. Расстояние от центра масс маятника до точки подвеса может изменяться в небольших пределах ( см) вращением узла крепления гири к стержню. При необходимости такой регулировки пригласите преподавателя или инженера.
см) вращением узла крепления гири к стержню. При необходимости такой регулировки пригласите преподавателя или инженера. между точкой крепления пружины к маятнику и осью вращения в соответствии с индивидуальным заданием.
между точкой крепления пружины к маятнику и осью вращения в соответствии с индивидуальным заданием. и
и  в режиме биений. Величину
в режиме биений. Величину  , выберите в соответствии с индивидуальным заданием. При расчетах примите: m= 1кг, l= 1 м, k= 3 Н/м. Постройте графики
, выберите в соответствии с индивидуальным заданием. При расчетах примите: m= 1кг, l= 1 м, k= 3 Н/м. Постройте графики  2.
2. ,
,  , рис. 2б) ось пружины при колебаниях остается практически горизонтальной (рис.1-1.). В этом случае суммарный момент сил тяжести
, рис. 2б) ось пружины при колебаниях остается практически горизонтальной (рис.1-1.). В этом случае суммарный момент сил тяжести  и упругости
и упругости  относительно оси вращения 1-го маятника равен
относительно оси вращения 1-го маятника равен ,
, - проекция силы
- проекция силы  на ось
на ось  ,
,  - деформация пружины. Момент сил, действующих на второй маятник, относительно его оси вращения равен
- деформация пружины. Момент сил, действующих на второй маятник, относительно его оси вращения равен ,
, ,
,  . При малых углах отклонения маятников от вертикали
. При малых углах отклонения маятников от вертикали  ,
,  , поэтому
, поэтому ,
,  .
.








 ,
,  ,
, - момент инерции каждого маятника относительно оси вращения. После сокращения получим
- момент инерции каждого маятника относительно оси вращения. После сокращения получим , (П1)
, (П1) ,
,  . Заметим, что величина
. Заметим, что величина  равна собственной частоте уединенного (несвязанного) маятника, а величина
равна собственной частоте уединенного (несвязанного) маятника, а величина  зависит от параметров маятника и пружины, ее называют коэффициентом связи системы.
зависит от параметров маятника и пружины, ее называют коэффициентом связи системы. , где
, где  . Общее решение этого уравнения имеет вид
. Общее решение этого уравнения имеет вид . (П2)
. (П2) , где
, где  ,
,  . Общее решение этого уравнения имеет вид
. Общее решение этого уравнения имеет вид . (П3)
. (П3) ,
, ,
,
 ,
,  .
.

 в процессе измерения
в процессе измерения
 (контролируются приборами на рис. 2-3) в одну сторону от вертикали и одновременно отпустите. Измерения начинайте примерно через 30 с после начала колебаний, когда колебательный процесс установится. Запись колебаний должна происходить не менее двух-трех минут. После завершения измерений на экране отображаются графики колебаний. Выбирая входы 1 или 2, путем нажатия на кнопки U1 или U2, можно наблюдать на экране монитора графики колебаний каждого маятника в отдельности или сразу оба графика. Для одинаковых маятников и одинаковых начальных условий кривые
(контролируются приборами на рис. 2-3) в одну сторону от вертикали и одновременно отпустите. Измерения начинайте примерно через 30 с после начала колебаний, когда колебательный процесс установится. Запись колебаний должна происходить не менее двух-трех минут. После завершения измерений на экране отображаются графики колебаний. Выбирая входы 1 или 2, путем нажатия на кнопки U1 или U2, можно наблюдать на экране монитора графики колебаний каждого маятника в отдельности или сразу оба графика. Для одинаковых маятников и одинаковых начальных условий кривые  и
и  должны практически совпадать. Если это не так, обратитесь к инженеру или преподавателю.
должны практически совпадать. Если это не так, обратитесь к инженеру или преподавателю. , пользуясь для повышения точности инструментами «Обзор» и «Лупа» (рис.2-4). Оцените погрешность измерения
, пользуясь для повышения точности инструментами «Обзор» и «Лупа» (рис.2-4). Оцените погрешность измерения  . При необходимости проконсультируйтесь по этому вопросу с преподавателем или инженером.
. При необходимости проконсультируйтесь по этому вопросу с преподавателем или инженером. противофазных колебаний, отклоняя маятники на равные углы в противоположные стороны от положения равновесия.
противофазных колебаний, отклоняя маятники на равные углы в противоположные стороны от положения равновесия. ,
, 
 .
. ).
).


 и
и  и противофазных
и противофазных  колебаний.
колебаний.


