
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для нефизических специальностейСодержание книги Поиск на нашем сайте
МЕХАНИКА Учебно-методический комплекс по дисциплине Для нефизических специальностей Лабораторный практикум Абакан ББК 22.2я73 УДК 531 (07) М55 Печатается по рекомендации Методического совета И по решению Редакционно-издательского совета ФГБОУ ВПО «Хакасский государственный университет Им. Н. Ф. Катанова»
М55 Механика: учебно-методический комплекс по дисциплине для нефизических специальностей. Лабораторный практикум / сост. С. Л. Гафнер, Л. В. Редель, Ю. Я. Гафнер. – Абакан: Издательство ФГБОУ ВПО «Хакасский государственный университет им. Н. Ф. Катанова». – 2011. – 73 с.
В пособии приводятся описания 14 лабораторных работ раздела «Механика» по дисциплине «Физика» для нефизических специальностей. В описании каждой лабораторной работы рассматриваются теоретические основы изучаемого явления, раскрывается методика его экспериментального исследования, даются рекомендации по обработке и анализу полученных результатов, приводятся контрольные вопросы и список рекомендуемой литературы. Пособие предназначено для студентов, обучающихся по специальностям «Биоэкология», «Городское строительство и хозяйство», «Технология и предпринимательство», «Информационные системы и технологии» и др., а также для направлений подготовки «Информатика и вычислительная техника», «Агрономия» и многих других бакалавров.
© ФГБОУ ВПО «Хакасский государственный университет им. Н. Ф. Катанова», 2011 © С. Л. Гафнер, Л. В. Редель, Ю. Я. Гафнер, составление, 2011 ПРЕДИСЛОВИЕ В данном пособии обобщен многолетний опыт кафедры общей и экспериментальной физики Хакасского государственного университета им. Н. Ф. Катанова по организации и проведению лабораторного практикума по механики в рамках курса физики для нефизических специальностей. Содержание лабораторного практикума соответствует программам высшего профессионального образования по специальностям: 020803 - Биоэкология, 270105 - Городское строительство и хозяйство, 230201 - Информационные системы и технологии и др., а также для направлений подготовки 230100 - Информатика и вычислительная техника, 110200 – Агрономия, 050100 - Технология и многих других бакалавров. Направленность лабораторного практикума определяется, прежде всего, изучением наиболее общих вопросов механики, использования значительного количества разнообразных физических приборов и оборудования. Описание лабораторных работ и контрольные вопросы составлены таким образом, чтобы стимулировать самостоятельную работу студентов с дополнительной литературой. В целях более правильного сочетания проведения лабораторных работ и чтения лекционного курса лабораторные работы, описанные в данном пособии, группируются по циклам. В процессе подготовки к лабораторной работе студент должен заранее познакомиться с ее описанием, теорией изучаемого явления и подготовить бланк отчета. На бланке указываются название лабораторной работы, ее цели, перечень используемых принадлежностей, приводится схема экспериментальной установки. Записываются рабочие формулы с расшифровкой всех величин, входящих в них, чертится таблица измеряемых величин. Перед проведением эксперимента студент должен получить допуск к работе. Для этого необходимо предоставить преподавателю подготовленный бланк отчета и ответить на контрольные вопросы по теории исследуемого явления, а также на вопросы по содержанию лабораторной работы и методики эксперимента. В отчете по лабораторной работе должны быть приведены примеры расчета исследуемых величин, необходимые графики, оценки погрешностей измерения. В конце отчета формулируются выводы относительно выполнения целей работы, соответствия экспериментальных результатов табличным данным или теоретическим оценкам. Оформленный отчет должен быть предоставлен преподавателю на следующем занятии.
Лабораторная работа 1 Введение Одной из важнейших характеристик твердых тел в механике является их масса. Различают инертную массу тел, которая служит мерой инертности тел (тела с большей массой ускоряются медленнее, чем тела с меньшей массой при действии на них одинаковой силы) и гравитационную массу, которая характеризует интенсивность притяжения объектов друг к другу по закону всемирного тяготения. В настоящее время считают, что с очень высокой степенью точности инертная и гравитационная массы совпадают. Притяжение тел к Земле приводит к тому, что тела начинают действовать с определенными силами на опоры или подвесы, на которых они закреплены. Сила, с которой тело действует на опору или подвес, называется весом тела. Вес тела в основном определяется его массой (в простейшем случае Различные тела могут иметь одинаковые массы и, следовательно, весить одинаково, при этом геометрические размеры их могут сильно отличаться. Отношение массы тела m к его объему V называется плотностью:
Плотность является важной величиной, характеризующей материал, из которого изготовлено данное тело. Она зависит от массы атомов, из которых состоит тело, и от плотности упаковки атомов в веществе. Одно и то же вещество в разных агрегатных состояниях имеет разную плотность: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Правда, вода является исключением из этого правила, её плотность при затвердевании уменьшается. Плотности некоторых веществ приведены в таблице 1.1. Таблица 1.1
Для расчета плотности твердого тела по формуле (1.1) необходимо знать массу тела m и его объем V. Масса тела может быть измерена при помощи весов:
где Р – вес тела и g (≈ 9,81 м/с2) – ускорение свободного падения. Обычно шкала весов уже проградуирована в единицах массы (килограммах). Определение объема твердого тела представляет собой более сложную задачу. Можно воспользоваться методом Архимеда, т.е. приравнять объем твердого тела к объему жидкости, вытесненной этим телом. Для тел правильной геометрической формы (цилиндр или параллелепипед) объем тела может быть рассчитан. Так, объем тела цилиндрической формыравенпроизведению площади его основания на высоту:
где R – радиус и D – диаметр основания цилиндра; h – его высота. Объем тела в форме прямоугольного параллелепипеда равен: V = а b с, (1.4) где а, b и с – стороны параллелепипеда. Подставляя соотношения (1.3) и (1.4) в формулу (1.1), получим рабочие формулы для расчёта плотностей:
и
Описание приборов Для повышения точности измерения масштабные линейки дополняются специальной шкалой – нониусом (линейным или круговым). Нониус изготавливают так, что длина N делений на нониусе равна длине kN – 1 делений основной шкалы: а н N = а ш (kN – 1), (1.7) где k – целое число (k = 1,2,3…), а ш и а н – длина малого деления основной шкалы и нониуса соответственно. Наименьшая длина, которую можно измерить с помощью масштабной линейки с нониусом, равна
При измерении внешних размеров детали рамку 2 смещают и зажимают деталь губками 3 или 4. Положение рамки при этом фиксируется винтами 5 и 6. Затем снимают отсчет: по основной шкале определяют измеряемую длину с точностью до 1 мм (она равна числу целых миллиметровых делений, расположенных слева от нуля нониуса) и прибавляют число сотых долей миллиметра по шкале нониуса (оно равно точности нониуса, умноженной на номер деления нониуса, совпадающего с одним из делений основной шкалы). Губками 4 можно измерять внутренние размеры детали, диаметры цилиндрических выемок, внутренние диаметра труб и т.д. В этих случаях к отчету, снятому по основной шкале и нониусу, прибавляют суммарную ширину губок, которая указана на этих губках. Перед началом измерений следует познакомиться с нониусом штангенциркуля (определить число делений нониуса, скольким делениям основной шкалы соответствуют все деления нониуса; вычислить точность нониуса). Технические весы. Это рычажные весы типа ВТ – 2 – 200 (рис. 1.2). Предельная нагрузка весов – 200 г. Максимальная (допустимая) погрешность при такой нагрузке – 50 мг. Основная часть весов – коромысло 1 со стрелкой 2. Посередине коромысла имеется опорная призма, по краям – сережки 3 с подвесками и чашками. Винты с гайками 4 служат для ре Взвешивание на рычажных весах – это определение массы тела путем её сравнения с массой эталонного груза – разновеса. Процесс взвешивания состоит из последовательных операций уравновешивания весов и включает следующие этапы: 1. Подготовка весов к взвешиванию – установка весов по отвесу и уравновешивание коромысла ненагруженных весов с помощью гаек 4. Часто считают, что весы уравновешены, если при разарретировании стрелка 2 отклоняется приблизительно на равные расстояния от среднего деления шкалы 9 (это взвешивание в грубом приближении). 2. Взвешивание: на левую чашку арретированных весов помещают взвешиваемое тело, на другую – пинцетом разновес, добиваясь такого же равновесия, как и в случае ненагруженных весов. При этом испытывают гирьки разновеса, начиная с наибольшей в той последовательности, в которой они уложены в коробке разновеса. Примечание: 1. Более точное определение точки равновесия весов производится методом отсчета отклонений стрелки 2 влево и вправо от нуля шкалы 9. 2. В момент снятия и накладывания грузов и разновеса на чашки весы обязательно арретируются. Не допускается раскачивание чашек при взвешивании, загрязнение и т.д. Оценка точности взвешивания: в грубом приближении за точность измерения массы можно принять разность масс тела, полученных при взвешивании с избытком и недостатком. При этом, если в уравновешенных нагруженных весах положение равновесия стрелки 2 немного смещено вправо от середины шкалы 9, то масса определена с недостатком (m Н), если влево – то с избытком (m И). Погрешность измерения массы равна для этого случая Измерения и обработка результатов Упражнение 1. Определение плотности тела неправильной формы. 1. Ознакомиться с устройством технических весов и правилами взвешивания. 2. Взвесить на технических весах образец. 3. Определить объём образца с помощью мензурки. 4. Рассчитать плотность образца по формуле (1.1). 5. Оценить абсолютную (Δ ρ) и относительную (ερ) погрешности измерений, используя формулы:
6. Записать результат с учётом погрешности в следующем виде:
7. Сравнить полученное значение плотности с табличными значениями плотностей различных веществ и определить материал, из которого изготовлен образец.
Упражнение 2. Определение плотности тела правильной формы (цилиндр или параллелепипед). 1. Ознакомиться с устройством штангенциркуля и определить точность его нониуса. 2. Измерить линейные размеры предложенного образца (не менее 3-х раз в различных точках). 3. Взвесить на технических весах образец. Данные прямых измерений занести в таблицу 1.1. Таблица 1.1
4. Рассчитать плотность образца с помощью формул (1.5) или (1.6). 5. Оценить абсолютную (Δ ρ) и относительную (ερ) погрешности измерений, используя формулы:
6. Записать результат с учётом погрешности в следующем виде:
7. Сравнить полученное значение плотности с табличными значениями плотностей различных веществ и определить материал, из которого изготовлен образец.
Контрольные вопросы 1. Что такое масса тела и чем она отличается от веса тела? 2. Зависят ли масса тела и вес тела от широты местности и почему? 3. Что такое плотность твердого тела и что она характеризует? 4. Что такое прямые и косвенные измерения? 5. Дайте определение нониуса и его точности. 6. Расскажите об устройстве и правилах использования штангенциркуля. 7. Расскажите об устройстве технических весов и правилах взвешивания на них. 8. Как определить точность взвешивания на технических весах в грубом приближении? Какова погрешность взвешивания в этом случае?
Лабораторная работа 2 ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ Введение Распределение массы в пределах тела можно охарактеризовать с помощью величины, называемой плотностью. Если тело однородно, т.е. свойства его во всех точках одинаковы, то плотностью называется величина, равная:
где m – масса тела, а V – его объём. Для тела с неравномерно распределенной массой выражение (2.1) дает среднюю плотность. В этом случае плотность в точке тела определяется следующим образом:
где Δ m – масса, заключенная в объёме Δ V. Предельный переход в этом выражении нельзя понимать так, что объём Δ V стягивается буквально в точку. Уменьшение Δ V следует осуществлять до тех пор, пока ещё не обнаруживается атомная структура вещества. Поэтому под dV в (2.2) надо подразумевать физически бесконечно малый объём, который, с одной стороны, достаточно мал для того, чтобы макроскопические (т.е. присущие большой совокупности атомов) свойства вещества можно было считать в его пределах одинаковыми, а с другой стороны, достаточно велик для того, чтобы не могла проявляться дискретность (прерывность) вещества. Согласно (2.2) элементарная масса dm равна произведению плотности ρ тела в данной точке на соответствующий элементарный объём dV: dm = ρdV. (2.3) Тогда масса всего тела равна:
где интегрирование распространяется на весь объём V тела. Введя понятие плотности вещества, необходимо раскрыть его практическое значение. Определение плотности вещества на практике имеет разное назначение. Это связано с тем, что во многих случаях с изменением составных частей сложного вещества происходит изменение плотности этого вещества. Поэтому оказывается возможным по величине плотности судить о том, состоит ли данное тело из одного вещества или содержит примеси других. В сложных, например, органических веществах по плотности можно определить процентное содержание составляющих веществ. Так, по плотности молока определяют процентное содержание в нем жира и белков. Существует также определенная зависимость плотности картофеля от количества содержащихся в нем крахмала и белков. Учитывая характер этой зависимости, по плотности картофеля определяют процентное содержание в нем крахмала. Последнее дает возможность решить вопрос о том, где целесообразнее использовать данный сорт картофеля. Картофель, содержащий крахмал менее 20 % от массы всего клубня, идет на корм скоту. Картофель с большим содержанием крахмала, лучше использовать для технических целей, например, для переработки на крахмал и патоку. Почти с такой же крахмалистостью нужен картофель и для питания человека.
Теория метода измерений В данной лабораторной плотности тела определяется по формуле (2.1). Масса и объём, необходимые для нахождения плотности пшеницы, картофеля и жидкости, измеряются экспериментально с помощью весов и мензурки. Нахождение массы сыпучих веществ и растворов можно производить несколькими способами. Можно определить массу образца взвешиванием его в сосуде с известной массой (если масса сосуда не известна, то её необходимо найти). В этом случае масса тела (m т) равна: m т = m п – m с (2.5) где m п – масса сосуда вместе с телом, и m с – масса сосуда, в котором взвешивают образец. Другой способ заключается в том, что массой сосуда можно пренебречь, если масса тела велика по сравнению с массой сосуда. Например, сыпучие вещества массой 100 г насыпают в полиэтиленовый пакет. Массу жидких веществ можно определить этими же двумя способами, а массу картофеля – путем взвешивания клубня на весах. При определении объема твердого тела можно воспользоваться методом Архимеда, т.е. приравнять объем твердого тела к объему жидкости, вытесненной этим телом. Тогда объём картофеля: Δ V = V 1 – V 0, (2.6) где V 0 – объём жидкости в мензурке до погружения картофеля, а V 1 – объём, занимаемый жидкостью вместе с погруженным в нее картофелем. Объёмы сыпучих веществ и жидкости определяется с помощью мерного стакана.
Измерения и обработка результатов 1. Ознакомиться с устройством технических весов и правилами взвешивания (см. лабораторную работу 1). 2. Определить массу, объём и плотность сельскохозяйственных продуктов. Результаты измерений и вычислений занести в таблицу 2.1. Таблица 2.1
3. Определить процентное содержание крахмала в картофеле (см. приложение 2). Сделать вывод о целесообразности использования данного сорта картофеля. 4. Определить насыпную плотность пшеницы. Полученное значение плотности сравнить с табличным (ρ пш = 760 кг/м3) и сделать вывод о причинах отклонения от табличного значения. 5. Определить плотности растворов поваренной соли (NaCl) с различными концентрациями. Построить график зависимости плотности раствора от концентрации NaCl в этом растворе.
Контрольные вопросы 1. Что такое плотность твердого тела и что она характеризует? 2. Что такое прямые и косвенные измерения? 3. Расскажите об устройстве технических весов и правилах взвешивания на них. 4. Как определить точность взвешивания на технических весах в грубом приближении? Какова погрешность взвешивания в этом случае? 5. Где можно применять на практике в сельском хозяйстве знание плотности вещества? ЦИКЛ 2. КИНЕМАТИКА ЗАКОНЫ СОХРАНЕНИЯ Лабораторная работа 3 С ПОМОЩЬЮ МАШИНЫ АТВУДА
Цели работы: изучение законов движения грузов на машине Атвуда и ознакомление с простейшими методами экспериментальной проверки функциональной зависимости между измеряемыми величинами. Приборы и принадлежности: машина Атвуда, набор дополнительных грузов, секундомер. Библиографический список: [1] § 3; [2] ч.1 § 4, § 5; [3] т.1 § 4; [4] т.1 § 2; [5] § 1.5; [7] § 1.2.1; [8] § 2.
Введение
Справедливость уравнения (3.1) в данной работе можно проверить с помощью машины Атвуда двумя способами: 1. Графический метод. Теоретическая формула (3.1) является нелинейной (квадратичной) зависимостью между S и t. Но для переменной x = t 2 эта зависимость становится линейной, а ее график (в координатах S и t 2) – прямой, проходящей через начало координат. Следовательно, если график, построенный по результатам измерений в координатах S и t 2, можно представить в виде прямой, проходящей через начало координат, то для движения грузов справедлива проверяемая формула (3.1), движение грузов является равноускоренным и можно вычислить ускорение а. 2. Аналитический метод. Проверка формулы (3.1) без построения графика заключается в том, что в ходе эксперимента для различных расстояний S 1, S 2, S 3, S 4 проходимых грузами под действием одинаковой силы (m п = const) вычисляются ускорения а 1, а 2, а 3, а 4 по формуле (3.1). Если их отклонения (относительные погрешности) от среднего значения а ср не превосходят 10 %, то в пределах такой погрешности эти ускорения можно считать одинаковыми, а движение – равноускоренным и проверяемую формулу справедливой.
Лабораторная работа 4 Введение Рассмотрим движение системы, состоящей из двух тел одинаковой массы М с перегрузком m на одном из них; тела подвешены к концам нити, перекинутой через блок (рис. 4.1).
(М + m) g – T 1 = (M + m) a 1 (4.1) Для второго тела: Т 2 – Mg = Ма 2 (4.2)
mg = (2 M + m) a. (4.3) Если силой трения пренебречь нельзя, то уравнение (4.3) примет вид: Mg – F тр = (2 M + m) a. (4.4) Если система тел начинает движение из состояния покоя, для перемещения S и скорости υ справедливы уравнения:
υ = аt. (4.6) Из (4.5) и (4.6) формул можно получить зависимость υ от S: υ 2 = 2 aS. (4.7)
Теория метода измерений Проверка уравнения перемещения и определение мгновенной скорости Для проверки уравнения перемещения равноускоренного движения используют блок-схему на рисунке 4.3а, определения скорости – блок-схему на рисунке 4.3б. В обоих случаях равноускоренное движение вызывается одним и тем же перегрузком (перегрузками). При проведении лабораторной работы необходимо на правый груз поместить два перегрузка (m и m /). Требования к перегрузкам: нижний перегрузок, например, m / должен компенсировать силу трения в оси блока и нити о блок; линейные размеры верхнего перегрузка должны быть таковы, чтобы он не проходил через подвижное кольцо 6. Если трение хорошо скомпенсировано, то в случае блок-схемы (рис. 4.3б) движение правого груза 4 до кольца 6 равноускоренное, после кольца – равномерное. Очевидно, конечная скорость υ равноускоренного движения равна скорости υ * равномерного движения (υ = υ *), причем: υ = аt, (4.8)
Здесь t и t * – время движения правого груза до и после кольца, S * – перемещение груза после кольца. В данной работе мгновенную скорость определяют по формуле (4.9). Проверка второго закона Ньютона Рассмотрим движение системы грузов 4 с двумя перегрузками m 1 и m 2. Вначале поместим оба перегрузка на правый груз, затем меньший перегрузок (например, m 2) переложим на левый груз. При этом масса системы грузов 4 с перегрузками не изменится, а сила, действующая на эту систему, изменится. Из уравнения (4.4) для этих случаев имеем: (m 1 + m 2) g – F тр = (2 M + m 1 + m 2) а 1, (4.10) (m 1 – m 2) g – F тр = (2 M + m 1 + m 2) а 2. (4.11) Из (4.10) и (4.11):
Оставив перегрузки m 1 и m 2 на своих местах (m 2 на левом грузе, m 1 – на правом), уменьшим массу грузов 4 (отвинтим их нижние части). Сила трения при этом изменится (обозначим её F /тр). Из (4.4) для этого третьего случая получим: (m 1 – m 2) g – F /тр = (2 M / + m 1 + m 2) а 3. (4.13) Здесь 2 M / – масса грузов 4 без нижней части (облегченные грузы). Так как силы трения F тр и F/ тр малы по сравнению с (m 1 – m 2) g, то ими можно пренебречь. Тогда сила, действующая на систему грузов 4 во втором и третьем случаях, одинакова. Поэтому из (4.11) и (4.13):
Проверка второго закона Ньютона сводится к проверке равенств (4.12) и (4.14). Лабораторная работа 5 ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ
Цель работы: определение скорости пули с помощью баллистического маятника. Приборы и принадлежности: баллистический маятник, баллистический пистолет и пуля, сантиметровая шкала, технические весы с разновесом. Библиографический список: [1] § 9, § 13, § 15; [2] ч.1 § 9, § 18; [3] т.1 § 24, § 27–28; [4] т.1 § 4 - 6; [5] § 2.9, § 4.1, § 4.5; [7] § 1.4.1; [8] § 16, § 21.
Введение Баллистический маятник – симметричное массивное тело, подвешенное на практически нерастяжимых нитях (рис. 5.1). Рассмотрим систему: баллистический маятник – пуля. Начальное состояние этой системы: маятник висит на нитях, пуля летит вдоль оси симметрии маятника со скоростью При неупругом центральном ударе пули и маятника по закону сохранения импульса имеем:
Если период маятника намного больше времени взаимодействия маятника с пулей, он успевает отклониться от положения равновесия и начинает движение из этого положения со скоростью
где М и m – массы маятника и пули, h – максимальная высота подъема маятника с пулей. Из (5.1) и (5.2) следует
Лабораторная работа 6 Введение Свободным падением называют движение в вакууме под действием только силы тяжести. Ускорение тела в этом случае называют ускорением свободного падения. По второму закону Ньютона:
где F T – сила тяжести тела массой m. Траектория, перемещение и скорость при свободном падении зависят от начальной скорости υ 0. При υ 0 = 0 тело, находящееся на высоте H и представленное самому себе, движется по вертикали. Тогда его перемещение (высота H) и конечная скорость υ равны:
В общем случае значение g зависит от высоты h над поверхностью Земли и широты φ местности. Ускорение свободного падения на полюсе (φ = π/2) максимально, а на экваторе (φ = 0) минимально:
Здесь M, R, ω –соответственно масса, радиус и угловая скорость вращения Земли. Относительное изменение g при переходе с полюса на экватор составляет примерно 0,3% от g max. Вследствие сплюснутости Земли g изменяется дополнительно сширотой. В итоге ускорение свободного падения g изменяется от 9,730 м/с2 (на экваторе) до 9,832 м/с2 (на полюсе). Для Абакана (φ = 56°) g = 9,82 м/с2. Значение g = 9,81 м/с2 принято за стандартное (табличное). Правила работы с установкой для определения ускорения свободного падения 1. Проверить работоспособность счётчика-секундомера: а) подключив к секундомеру электромагнит 4 и датчик 3, включить секундомер; б) нажать сначала на клавишу «СЕТЬ» (остальные клавиши должны быть в отжатом состоянии), а затем на клавишу «ПУСК» (при этом должен начаться отсчёт времени на табло 8); в) прервать луч датчика (отсчёт времени должен прекратиться); г) нажать на кнопку «СБРОС» (табло 8 должно вернуться в исходное состояние). 2. Вращая кронштейн 6, и перемещая штатив с датчиком, добиться правильного расположения электромагнита 4 относительно датчика 3 (использовать отвес 13). При правильном положении электромагнита на нити отвеса виден световой зайчик. Затем отодвинуть отвес. 3. Нажать на клавишу «СЕТЬ» и подвесить шарик 7 к электромагниту. 4. Нажать на клавишу «ПУСК» и снять показания со светового табло 8 после прекращения отсчёта времени (причина последнего – пересечение светового луча датчика падающим шариком). Если шарик не прервёт луч необходимо нажать последовательно на клавиши «СТОП» и «СБРОС», а затем повторить пункт 2. 5. Сняв показания отсчёта времени, нажать на клавишу «СБРОС» (вернув тем самым счётчик секундомер в исходное состояние). 6. По окончании измерений все клавиши счётчика-секундомера должны быть в отжатом положении. Прибор отключить от сети.
Лабораторная работа 7 ИЗУЧЕНИЕ ДЕФОРМАЦИИ ИЗГИБА
Цели работы: получить зависимость прогиба от нагрузки и представить эту зависимость графически; вычислить модуль Юнга. Приборы и принадлежности: Прибор ФП – 3А (для изучения деформации изгиба) с набором гирь; линейка метровая; штангенциркуль. Библиографический список: [1] § 21; [2] ч.1 § 10, § 54; [3] т.1 § 14; [4] т.1 § 49; [5] § 6.1–6.3; [7] § 1.3.4.
Введение Важным примером деформации твердого тела является изгиб стержня (рис. 7.1) под действием поперечных нагрузок (сил, приложенных перпендикулярно к оси стержня). При такой деформации верхние слои стержня удлиняются, нижние сжимаются, а длина центрального слоя остается неизменной (ОО1/ =
В общем случае причиной изгиба стержня является действие двух сил: силы тяжести самого стержня и внешней силы. Для упругого изгиба прогиб стержня
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.10.139 (0.015 с.) |

 ), для определения массы тел их обычно взвешивают.
), для определения массы тел их обычно взвешивают. . (1.1)
. (1.1) , (1.2)
, (1.2) , (1.3)
, (1.3) (цилиндр) (1.5)
(цилиндр) (1.5) (параллелепипед). (1.6)
(параллелепипед). (1.6) . Её называют точностью нониуса. Обычно значение Δ указывают рядом со шкалой нониуса.
. Её называют точностью нониуса. Обычно значение Δ указывают рядом со шкалой нониуса. Штангенциркуль. Штангенциркулем измеряют линейные размеры тел небольших длин, когда измерения не требуют высокой точности. Основная часть штангенциркуля (рис. 1.1) – линейка 1 с масштабом. Вдоль линейки скользит подвижная рамка 2, на которой нанесены деления нониуса.
Штангенциркуль. Штангенциркулем измеряют линейные размеры тел небольших длин, когда измерения не требуют высокой точности. Основная часть штангенциркуля (рис. 1.1) – линейка 1 с масштабом. Вдоль линейки скользит подвижная рамка 2, на которой нанесены деления нониуса. На линейке имеются измерительные выступы – губки 3 и 4. У разных штангенциркулей количество их различно. Если губки 3 и 4 сдвинуты вплотную, нули нониуса и основной шкалы совпадают.
На линейке имеются измерительные выступы – губки 3 и 4. У разных штангенциркулей количество их различно. Если губки 3 и 4 сдвинуты вплотную, нули нониуса и основной шкалы совпадают. гулировки равновесия коромысла. При измерениях массы коромысло опускается острием опорной призмы на стальную подушку, находящуюся в верхней части колонки 5. В отсутствии измерений коромысло немного приподнимают, тем самым предохраняют опорную призму от изнашивания. Подъем и опускание коромысла осуществляют ручкой 6 специального устройства – арретира.
гулировки равновесия коромысла. При измерениях массы коромысло опускается острием опорной призмы на стальную подушку, находящуюся в верхней части колонки 5. В отсутствии измерений коромысло немного приподнимают, тем самым предохраняют опорную призму от изнашивания. Подъем и опускание коромысла осуществляют ручкой 6 специального устройства – арретира.  Для этого ручку 6 поворачивают до упора влево или вправо (весы разарретированы), затем до упора в другую сторону (весы арретированы, т.е. в нерабочем состоянии). Уравнительные винты 7 обеспечивают вертикальность колонки 5; что контролируется отвесом 8.
Для этого ручку 6 поворачивают до упора влево или вправо (весы разарретированы), затем до упора в другую сторону (весы арретированы, т.е. в нерабочем состоянии). Уравнительные винты 7 обеспечивают вертикальность колонки 5; что контролируется отвесом 8. . Если стрелка остановилась на «0» – делении, то
. Если стрелка остановилась на «0» – делении, то  .
. ,
, .
.
 для параллелепипеда,
для параллелепипеда, для цилиндра,
для цилиндра, .
. .
. , (2.1)
, (2.1) , (2.2)
, (2.2) , (2.4)
, (2.4) Рассмотрим движение системы 2-х тел одинаковой массы m, которые подвешены к концам нити, перекинутой через блок (рис. 3.1). Грузы могут двигаться вдоль вертикального направления. Если на один из грузов положить небольшой добавочный груз (перегрузок) массой m п, то грузы начнут двигаться с ускорением а под действием силы тяжести. Такое движение называют равноускоренным, т.е. движение с постоянным по модулю и направлению ускорением (
Рассмотрим движение системы 2-х тел одинаковой массы m, которые подвешены к концам нити, перекинутой через блок (рис. 3.1). Грузы могут двигаться вдоль вертикального направления. Если на один из грузов положить небольшой добавочный груз (перегрузок) массой m п, то грузы начнут двигаться с ускорением а под действием силы тяжести. Такое движение называют равноускоренным, т.е. движение с постоянным по модулю и направлению ускорением ( ).
). Если система тел начинает движение из состояния покоя, то пройденный системой путь S за время t определяется формулой:
Если система тел начинает движение из состояния покоя, то пройденный системой путь S за время t определяется формулой: . (3.1)
. (3.1) Описание экспериментальной установки
Описание экспериментальной установки Установка, называемая машиной Атвуда (рис. 3.2), представляет собой вертикальную стойку с сантиметровой шкалой 1 и регулировочными винтами 2. На верхнем конце стойки прикреплен легкий пластмассовый блок 3, через который переброшена нить с подвешенными на концах грузами m 1 и m2. Массы грузов примерно одинаковы, за счет трения в блоке система находится в равновесии. Для того, чтобы привести систему грузов в движение, на правый груз кладут перегрузок m п. Опуская левый груз, устанавливают начальное положение правого груза на определенном делении шкалы. Время движения грузов определяется с помощью механического секундомера. Для начала измерения опускают левый груз и одновременно включают секундомер. Момент отключения секундомера должен совпадать со звуком удара правого груза о дно приемного столика 4.
Установка, называемая машиной Атвуда (рис. 3.2), представляет собой вертикальную стойку с сантиметровой шкалой 1 и регулировочными винтами 2. На верхнем конце стойки прикреплен легкий пластмассовый блок 3, через который переброшена нить с подвешенными на концах грузами m 1 и m2. Массы грузов примерно одинаковы, за счет трения в блоке система находится в равновесии. Для того, чтобы привести систему грузов в движение, на правый груз кладут перегрузок m п. Опуская левый груз, устанавливают начальное положение правого груза на определенном делении шкалы. Время движения грузов определяется с помощью механического секундомера. Для начала измерения опускают левый груз и одновременно включают секундомер. Момент отключения секундомера должен совпадать со звуком удара правого груза о дно приемного столика 4. Без учета трения второй закон для первого тела запишется в виде:
Без учета трения второй закон для первого тела запишется в виде: Если нить нерастяжима, а массами нити и блока можно пренебречь, то грузы движутся с одинаковыми ускорениями и силы натяжения, действующие на грузы, одинаковы. Отсюда из (4.1) и (4.2) получим:
Если нить нерастяжима, а массами нити и блока можно пренебречь, то грузы движутся с одинаковыми ускорениями и силы натяжения, действующие на грузы, одинаковы. Отсюда из (4.1) и (4.2) получим: , (4.5)
, (4.5) . (4.9)
. (4.9) . (4.12)
. (4.12) . (4.14)
. (4.14) . Конечное состояние: маятник с застрявшей в нём пулей максимально отклонился от положения равновесия на угол α, центр тяжести С маятника поднялся на высоту h (рис. 5.2а).
. Конечное состояние: маятник с застрявшей в нём пулей максимально отклонился от положения равновесия на угол α, центр тяжести С маятника поднялся на высоту h (рис. 5.2а). . (5.1)
. (5.1) . Это движение маятника с пулей, застрявшей в нём. Оно в отсутствие сопротивления воздуха и трения в подвесе маятника происходит в соответствии с законом сохранения механической энергии:
. Это движение маятника с пулей, застрявшей в нём. Оно в отсутствие сопротивления воздуха и трения в подвесе маятника происходит в соответствии с законом сохранения механической энергии: , (5.2)
, (5.2)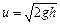 . (5.3)
. (5.3) , (6.1)
, (6.1) , (6.2)
, (6.2) . (6.3)
. (6.3) , (6.4)
, (6.4) . (6.5)
. (6.5) ОО1). Все поперечные сечения наклоняются в сторону изгиба и остаются плоскими.
ОО1). Все поперечные сечения наклоняются в сторону изгиба и остаются плоскими. Отклонение (y) точки с координатой x от прямой, на которой лежала эта точка до деформации, называется прогибом, максимальный прогиб y m – «стрелой» прогиба (рис 7.1).
Отклонение (y) точки с координатой x от прямой, на которой лежала эта точка до деформации, называется прогибом, максимальный прогиб y m – «стрелой» прогиба (рис 7.1).


