
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение (1.11) с учетом (1.12) приметСодержание книги
Поиск на нашем сайте
Выражение (1.13) называется основным уравнением молекулярно - кинетической теории идеальных газов. Точный расчет с учетом движения молекул по всевозможным направлениям дает ту же формулу.
Так как масса газа m=Nm0, то уравнение (1.14) можно переписать в виде
Для одного моля газа m=M (M - молярная масса), поэтому
где Vm - молярный объем. С другой стороны, по уравнению Клапейрона-Менде-леева, pVm = RT. Таким образом,
откуда
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа
1.4. Закон Максвелла для распределения При выводе основного уравнения молекулярно-кинетической теории молекулам задавали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения молекул являются равновероятными, т.е. в любом направлении в среднем движется одинаковое число молекул. По молекулярно-кинетической теории, как бы не изменялась скорость молекул при столкновениях, средняя квадратичная скорость молекул массой m0 в газе, находящемся в состоянии равновесия при T=const, остается постоянной и равной При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют. Закон Максвелла описывается некоторой функцией f(
молекул
откуда
Применяя методы теории вероятности, Максвелл нашел функцию f(
Из (1.19) видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т). График функции (1.19) приведен на рис. 51.
Рис. 51 Он подтвержден экспериментально опытом Штерна. Т.к. при возраста- Относительное число молекул Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти продифференцировав выражение (1.19) по аргументу
Значения
Из формулы (1.20) следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис. 52) сместится вправо.
(средняя арифметическая скорость) определяется по формуле
Подставляя сюда f(
Скорости, характеризующие состояние газа: наиболее вероятная скорость
средняя средняя квадратичная
1.5. Среднее число столкновений и средняя длина Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Между этими последовательными столкновениями молекулы проходят некоторый путь l, который называется длиной свободнго пробera. В общем случае длина пути между последовательными столкновениями различна, но т. к. мы имеем дело с огромным числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул <
Так как за 1 с молекула проходит в среднем путь, равный средней арифметической скорости <
Для определения < z > представим себе молекулу в виде шарика диаметром d, которая движется среди других "застывших" молекул.
Эта молекула столкнется только c теми молекулами, центры котоpыx находятся на расстояниях, равных или меньших d, т.е. лежат внутри "ломаного" цилиндра радиусом d (pис. 54).
Рис. 54 Среднее число столкновений за 1 с равно числу молекул в объеме "ломаного" цилиндра: <z> = nV, где n - концентрация молекул, V=pd2 < <z>=npd2<
|
||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.110.253 (0.01 с.) |

 . (1.13)
. (1.13) , получим
, получим (1.14)
(1.14) , 0.15)
, 0.15)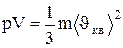 .
. ,
, ,
, . (1.16)
. (1.16)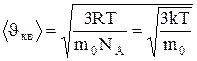 , (1.17)
, (1.17)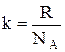 - постоянная Больцмана. Отсюда найдем, что при комнатной температуре молекулы кислорода имеют среднюю квадратичную скорость 480 м/с, водорода - 1900 м/с. При температуре жидкого гелия те же скорости будут соответственно 40 и 160 м/с.
- постоянная Больцмана. Отсюда найдем, что при комнатной температуре молекулы кислорода имеют среднюю квадратичную скорость 480 м/с, водорода - 1900 м/с. При температуре жидкого гелия те же скорости будут соответственно 40 и 160 м/с. (1.18)
(1.18) =0, т.е. при 0° К прекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газами формула (1.18) раскрывает молекулярно-кинетическое толкование температуры.
=0, т.е. при 0° К прекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газами формула (1.18) раскрывает молекулярно-кинетическое толкование температуры. . Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем, распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж.Максвеллом.
. Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем, распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж.Максвеллом. ), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные d
), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные d  , скорости которых лежат в интервале от
, скорости которых лежат в интервале от  ,
,
 . (1.19)
. (1.19)
 уменьшается быстрее, чем растет множитель
уменьшается быстрее, чем растет множитель  , скорости которых лежат в интервале от
, скорости которых лежат в интервале от 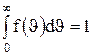 .
. .
.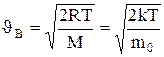 . (1.20)
. (1.20) Рис. 52
Рис. 52
 .
. . (1.21)
. (1.21) ;
; =1,13
=1,13  ;
;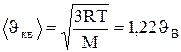 (рис.51).
(рис.51). >.
>. Рис. 53
Рис. 53
 .
.



