
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ускорение и его составляющиеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение. Рассмотрим плоское движение, т.е. такое, при котором все траектории точки лежат в одной плоскости. Пусть вектор Средним ускорением неравномерного движения в интервале от t до t+Δt называется векторная величина, равная отношению изменения скорости Δ
Мгновенным ускорением
Таким образом, ускорение
Вторая же составляющая вектора
т.е. равна первой производной по времени от модуля скорости и определяет тем самым быстроту изменения скорости по модулю. Найдем вторую составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому DS можно считать дугой окружности некоторого радиуса r, мало отличающегося от хорды АВ. Тогда из подобия треугольников АОВ и EAD следует то Поскольку
называется нормальной составляющей ускорения и направлена по нормали к траектории, к центру ее кривизны (поэтому ее называют также центростремительным ускорением). Полно е ускорение тела есть геометри-
ческая сумма тангенциальной и нормальной со ставляющих (рис.5):
Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения - быстроту изменения скорости по направлению (направлена к центру кривизны траектории). В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:
Проинтегрировав формулу ds =
|
|||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 2173; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.185.202 (0.007 с.) |

 задает скорость точки А в момент времени t. За время Δt движущаяся точка перешла в положение В и приобрела скорость, отличную от
задает скорость точки А в момент времени t. За время Δt движущаяся точка перешла в положение В и приобрела скорость, отличную от  . Перенесем вектор
. Перенесем вектор  в точку А и найдем Δ
в точку А и найдем Δ 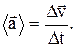
 (ускорением) материальной точки в момент времени t будет предел среднего ускорения:
(ускорением) материальной точки в момент времени t будет предел среднего ускорения: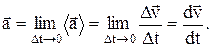

 , по модулю равный
, по модулю равный  , равный
, равный  , определяет изменение скорости по модулю за время Δt:
, определяет изменение скорости по модулю за время Δt:
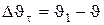 .
.
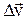 -
- 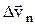 характеризует изменение скорости за время Δt по направлению.
характеризует изменение скорости за время Δt по направлению.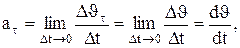
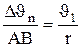 , но т.к. АВ =
, но т.к. АВ =  Δt,
Δt, В пределе при t®0 получим
В пределе при t®0 получим  .
.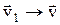 , угол EAD стремится к нулю, а т. к. треугольник EAD равнобедренный, то угол ADE между
, угол EAD стремится к нулю, а т. к. треугольник EAD равнобедренный, то угол ADE между 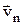 стремится к прямому. Следовательно, при t®0 векторы
стремится к прямому. Следовательно, при t®0 векторы  ,
,

 .
. = 0, аn =0 - прямолинейное равномерное движение;
= 0, аn =0 - прямолинейное равномерное движение;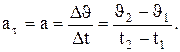 Если начальный момент времени t =0, а начальная скорость
Если начальный момент времени t =0, а начальная скорость 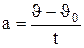 , откуда
, откуда 
 следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным;
следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным; - равномерное криволинейное движение;
- равномерное криволинейное движение; - криволинейное равнопеременное движение;
- криволинейное равнопеременное движение; - криволинейное движение с переменным ускорением.
- криволинейное движение с переменным ускорением.


