Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Траектория путь перемещение скорость ускорение определениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Линию, вдоль которой движется материальная точка, называют траекторией. Длину траектории называют путем. Единица пути — метр. Составляющие ускорения тангенциальное и нормальное ускорения Тангенциальное ускорение направлено по касательной к траектории
Нормальное ускорение направлено по нормали к траектории
Тангенциальное ускорение характеризует изменение скорости по величине. Если скорость по величине не изменяется, то тангенциальная составляющая равна нулю, а нормальная составляющая ускорения равна полному ускорению. Нормальное ускорение характеризует изменение скорости по направлению. Если направление скорости не изменяется, движение происходит по прямолинейной траектории.
В общем случае полное ускорение:
Итак, нормальная составляющая вектора ускорения
4) Угловой путь Угловой путь – это элементарный угол поворота:
Радиан – это угол, который вырезает на окружности дугу, равную радиусу.
Направление углового пути определяется правилом правого винта: если головку винта вращать в направлении движения точки по окружности, то поступательное движение острия винта укажет направление Угловая скорость (средняя и мгновенная) Средняя угловая скорость – это физическая величина, численно равная отношению углового пути к промежутку времени:
Мгновенная угловая скорость – это физическая величина, численно равная изменения пределу отношения углового пути к промежутку времени при стремлении данного промежутка к нулю, или является первой производной углового пути по времени:
Угловое ускорение (среднее и мгновенное) Среднее угловое ускорение – это физическая величина, численно равная отношению изменения угловой скорости к промежутку времени, за который это изменение произошло:
Мгновенное угловое ускорение – это физическая величина, численно равная пределу отношения изменения угловой скорости к промежутку времени при стремлении данного промежутка к нулю, или является первой производной угловой скорости по времени, или второй производной углового пути по времени:
При ускоренном движении угловое ускорение совпадает по направлению с угловой скоростью. При замедленном вращении угловое ускорение направлено в противоположную относительно угловой скорости сторону. Законы Ньютона Первый закон Ньютона
По сути, этот закон постулирует инерцию тел, что сегодня кажется очевидным. Но это было далеко не так на заре исследования природы. Аристотель вот утверждал, что причиной всякого движения является сила, т. е. движения по инерции для него не существовало. [ источник? ]
Второй закон Ньютона Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и её ускорением. Второй закон Ньютона утверждает, что
При подходящем выборе единиц измерения этот закон можно записать в виде формулы:
где
m — масса тела. Или в более известном виде:
Если на тело действуют несколько сил, то второй закон Ньютона записывается:
В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется в общем виде: скорость изменения импульса точки равна действующей на неё силе.
где t — время;
Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Третий закон Ньютона Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой Сам закон:
Выводы Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, надо потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел U (| r 1 − r 2 |). Тогда возникает закон сохранения суммарной механической энергии взаимодействующих тел:
Законы Ньютона являются основными законами механики. Из них могут быть выведены все остальные законы механики.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 5848; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.214.1 (0.011 с.) |




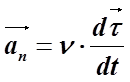
 быстрота изменения со временем направления касательной к траектории. Она тем больше (
быстрота изменения со временем направления касательной к траектории. Она тем больше ( ), чем больше искривлена траектория и чем быстрее перемещается частица по траектории.
), чем больше искривлена траектория и чем быстрее перемещается частица по траектории.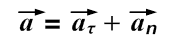
 ,
,  .
.
 .
. ,
, 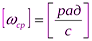 .
. ,
,  .
. ,
,  .
. ,
,  .
.
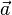 — ускорение тела;
— ускорение тела;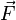 — сила, приложенная к телу;
— сила, приложенная к телу;


 — импульс (количество движения) точки;
— импульс (количество движения) точки; — производная по времени.
— производная по времени. , а второе — на первое с силой
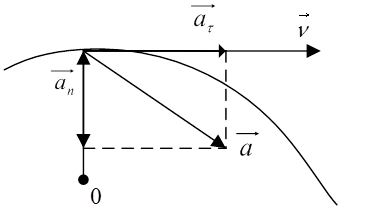
, а второе — на первое с силой  . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.