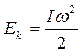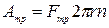Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет и измерение скорости шара, скатывающегося по наклонному желобуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Содержание
Введение Теория ошибок Расчет и измерение скорости шара, скатывающегося по наклонному желобу Исследование прямолинейного движения тел на машине Атвуда Изучение закона сохранения энергии. Сравнение изменения потенциальной энергии растянутой пружины с изменением кинетической энергии тела 6. Изучение закона сохранения момента импульса (вертушка) Измерение кинетической энергии вращающегося диска Изучение закона сохранения энергии. Измерение кпд наклонной плоскости Изучение основного уравнения динамики вращательного движения 10. Изучение движения тела, брошенного горизонтально ПРЕДИСЛОВИЕ
Техническая направленность в школьном образовании и повышение качества занятий учащихся физикой в значительной мере зависят от развития физического эксперимента и его широкого правильного применения в процессе обучения. Особое значение в накоплении действенных знаний имеет организация и выполнение физического практикума. Это пособие по экспериментальной физике для школьников X-XI классов, обучающихся в классах или школах физико-математического профиля. В нем приводятся описания физических опытов, предлагаемых учащимся для самостоятельного выполнения в форме лабораторных работ (практикума), а также рекомендации по обработке результатов измерений. Цели и задачи лабораторного практикума множественны. Во-первых, учащиеся должны приобрести определенную сумму знаний и практические навыки в области эксперимента, в частности по использованию ЭВМ в физических исследованиях. Во-вторых, в процессе выполнения практикума учащиеся знакомятся с устройством и действием различны экспериментальных установок и приборов, с методами измерений и способами обработки их результатов, с методами изучения физических процессов и установления количественных связей между физическими величинами (количественных законов). Все работы физического практикума для учащихся старших классов X – XI сгруппированы по темам в 5 учебных пособиях. - механика. - электричество, электромеханика, электромагнетизм. - молекулярная физика, термодинамика. - оптика. - колебания и волны. Учитель может по своему усмотрению предложить к выполнению весь практикум или отобрать какую-либо его часть. Каждое учебное пособие построено традиционно и состоит из цели работы, теоретических основ физических явлений, описание и фотографии экспериментальной установки, порядок проведения эксперимента. К каждой работе физического практикума даны контрольные вопросы и задачи для самоконтроля. В работах физического практикума использованы типовое физическое оборудование, а также оригинальные установки созданные авторами настоящего пособия. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ Случайные и систематические погрешности
Погрешности, возникающие при измерениях, делятся на систематические и случайные. Систематические погрешности — это погрешности, соответствующие отклонению измеренного значения физической величины от истинного значения всегда в одну сторону – либо в сторону завышения, либо в сторону занижения. При повторных измерениях в тех же условиях погрешность остается прежней. При закономерном изменении условий измерений погрешность также изменяется закономерно. Систематические погрешности могут возникать по ряду причин: 1) несоответствие средства измерения с эталоном (пластмассовые линейки с течением времени обычно укорачиваются; размеры, полученные при измерении такой линейкой, будут всегда завышены); 2) неправильная установка измерительного прибора (не уравновешены ненагруженные весы; амперметр установлен наклонно или боком); 3) пренебрежение поправками, которые следует внести в результаты измерений (например, в начальном положении стрелка измерительного прибора — секундомера, вольтметра — не совпадает с отметкой «0»); 4) несоответствие измеряемого объекта с предположениями о его свойствах (например, наличие скрытых пустот в теле, используемом для измерения плотности вещества). Систематические погрешности, обусловленные некоторыми из перечисленных причин, могут быть сведены к минимуму проверкой приборов, их тщательной установкой, анализом необходимых поправок и т. д. другие причины могут быть скрытыми в течение длительного времени и обнаруживаются при нахождении тех же физических величин принципиально другими методами. Случайные погрешности — это погрешности, которые непредсказуемым образом меняют свое численное значение и знак при повторных измерениях физической величины в одних и тех же контролируемых условиях (например, в приведенных выше измерениях длины бруска микрометром и взвешивании на аналитических весах). Случайные погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения. Такие причины могут быть объективными (неровности на поверхности измеряемого предмета; дуновение воздуха, ведущее к изменению температуры; скачкообразное изменение напряжения в электрической цепи и пр.) и субъективными (разная сила зажима предмета между ножками штангенциркуля; неодинаковое положение глаза относительно шкалы электроизмерительного прибора; различное запаздывание при включении и выключении секундомера). Эти причины могут сочетаться в различных комбинациях, вызывая то уменьшение, то увеличение значения измеряемой величины. Поэтому при нескольких измерениях одной и той же величины получается целый ряд значений этой величины, отличающихся от истинного значения случайным образом. Легко видеть, что влияние случайных погрешностей на результат измерений может быть существенно уменьшено при многократном повторении опыта.
Функциональные масштабы
В ряде случаев бывает заранее известен вид математической функции, выражающей исследуемую зависимость между физическими величинами. Такая зависимость может быть линейной (зависимость между деформацией пружины и растягивающей ее силой), квадратичной (зависимость от времени расстояния, пройденного телом при падении), показательной (зависимость сопротивления полупроводника от температуры) и т. д. На графиках такие зависимости изображаются известными геометрическими линиями: прямой, параболой, экспонентой и т. д. Однако пользуясь экспериментальными данными, можно с достаточной степенью достоверности построить лишь прямую. Проводя же плавную кривую между экспериментальными точками, нельзя поручиться, что получилась часть параболы, экспоненты или какой-либо другой линии. В таких случаях при построении графика целесообразно откладывать на координатных осях (или одной из них) не сами величины, между которыми определяется зависимость, а некоторые функции этих величин. Надлежащим выбором вида этих функций можно добиться, чтобы точки графика определяли прямую линию. Например, при изучении свободного падения тела предполагается, что результаты должны описываться законом
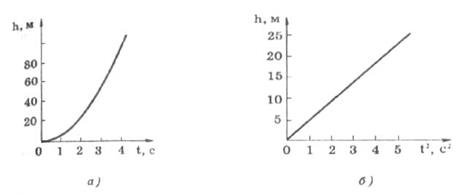
где h — расстояние, пройденное телом за время t; g — ускорение свободного падения. Если по осям откладывать h и t, то точки графика должны определять параболу (рис. 1.12а). Если же по осям откладывать соответственно h и t2, то графиком является прямая, проходящая через начало координат (рис. 1.12 б). Измерив угол наклона прямой, можно оценить значение ускорения свободного падения.
Рис. 1.12
Однако возможны такие функциональные зависимости, когда для исследуемой величины лучше применить логарифмический масштаб. Это необходимо, если исследуемая величина в рассматриваемых пределах изменения аргумента изменяется очень сильно (на несколько порядков, т. е. в сотни, тысячи, миллионы раз). Логарифмический масштаб позволяет весь график поместить на одном чертеже. Если вид математической функции, описывающей исследуемую зависимость, заранее неизвестен, то строят графики этой зависимости в различных функциональных масштабах; при этом можно найти такой из них, что график будет иметь вид прямой. В результате появляется возможность подобрать к исследуемой зависимости описывающую ее математическую функцию.
Оформление отчета о проделанной работе
Условно лабораторные работы можно разделить на измерительные и наблюдательные. Для каждого вида работ предлагаются единые формы отчета, приводимые ниже.
Измерительная лабораторная работа: 1) номер работы; 2) наименование работы; 3) цель работы; 4) чертеж (если требуется); 5) формулы для определения искомых величин и их погрешностей; 6) таблица с результатами измерений и вычислений; 7) окончательный результат, вывод и пр. (согласно цели работы).
Наблюдательная лабораторная работа: 1) номер работы; 2) наименование работы; 3) номер опыта; 4) цель опыта; 5) методика проведения опыта; 6) результаты наблюдения; 7) вывод; 8) общий вывод о проделанной работе (если требуется).
Лабораторная работа № 1
Теоретические основы работы
Для шара, скатывающегося с наклонного желоба высотой h, на основании закона сохранения энергии можно записать:
где т — масса шара, v и ω — линейная и угловая скорости шара в данный момент времени,
Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции относительно некоторой оси равен сумме произведений элементарных масс на квадрат расстояний до этой оси. Моменты инерций однородных тел простейшей формы легко выражаются через массу и геометрические характеристики. Второй закон Ньютона для вращательного движения имеет вид:
где L – момент импульса тела, величина равная произведению момента инерции тела на угловую скорость
Моменты инерции однородных тел простейшей формы относительно некоторых осей
Из рисунка видно, что при
Следовательно, первое равенство можно записать в виде:
Откуда
Поскольку скорость шара в любой момент времени пропорциональна корню квадратному из высоты h, движение шара — равноускоренное.
Порядок выполнения работы
1. С помощью уровня или шара установите горизонтальность поверхности стола. 2. С помощью штатива установите желоб в наклонном положении (рис. 2). Измерьте высоту h наклонного желоба. 3. Рассчитайте теоретическую скорость скатывания шара с желоба по формуле:
4. Измерьте длину l желоба и время t скатывания с него шара. 5. Рассчитайте скорость шара в конце желоба по формуле:
6. Повторите опыт при разных значениях высоты h наклонного желоба и сделайте вывод об оптимальных условиях выполнения работы. 7. Результаты измерений и расчетов занесите в отчетную таблицу.
Отчетная таблица
8. Рассчитайте погрешности измерений vT и vэ иубедитесь в достоверности измерений.
Рис. 2
Контрольные вопросы
1. Сформулируйте закон сохранения полной механической энергии. 2. Назовите условия при которых выполняется закон сохранения полной механической энергии. 3. Дайте определение момента инерции. 4. Почему при скатывании шара по желобу нельзя использовать формулу 5. Как доказать, что движение шара по желобу равноускоренное? 6. Чем объясняются различия в значениях v т и vэ, полученных в данной работе? 7. При каких углах наклона желоба погрешности измерений минимальны? 8. Какую роль играет трение в данном опыте? 9. Колесо катилось по столу со скоростью 0,6 м/с. Достигнув края стола стало падать. Определить скорость краевой точки через 0,02 с от начала падения (в этот момент её линейная скорость вращения направлена вертикально вниз). 10.Автомобиль движется со скоростью 10 м/с. Определить скорость относительно Земли точек A, B, C, лежащих на его ободе. 11.Два тела одновременно начинают движение по окружности из одной точки в одном направлении. Период обращения первого тела равен 3 с, второго 4 с. Через какой промежуток времени первое тело догонит второе? 12.Секундная стрелка в 2 раза короче минутной. Во сколько раз линейная скорость конца секундной стрелки больше линейной скорости минутной стрелки?
Творческий практикум Для точек земной поверхности на широте Санкт-Петербурга (60°) определите линейную скорость и ускорение, испытываемое ими вследствие суточного вращения Земли (рис. 33). Радиус Земли считайте равным 6370 км.
Лабораторная работа № 2
ИССЛЕДОВАНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ
Цель работы: Изучить равнопеременное и равномерное прямолинейные движения в поле земного тяготения. Определить ускорение свободного падения.
Оборудование: машина Атвуда.
Теоретические основы работы Механическим движением называется происходящее со временем перемещение тел или их частей относительно других тел (тел отсчета). Любое механическое движение рассматривается в определенной системе отсчета, состоящей из тела отсчета, связанной с ним системы пространственных координат и часов.
называют основным уравнением динамики. Эскиз машины Атвуда показан на рис.2. Два груза массами М соединены нитью, перекинутой через неподвижный блок. Если на один из грузов положить перегрузок массой m, то система приходит в ускоренное движение. Каждый из грузов натягивает участок нити, который, стараясь сократиться, действует на груз силой натяжения
а для другого груза:
Основное уравнение динамики вращательного движения неподвижного блока имеет вид:
где Если вращение по часовой стрелке считать положительным, то, согласно рис.2, получим
где R - радиус блока; Мтр - момент силы трения. Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:
Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:
Наконец, в отсутствие скольжения нити по блоку ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:
Проецируя уравнения (2) и (3) на ось У, направленную вертикально вверх, получим с учетом формул (5), (6) и (7) систему уравнений, к которой присоединим уравнение (4¢):
Умножая первое из уравнений (8) на -1 и складывая все уравнения (8), получим
В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство
Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:
Пренебрегая малыми величинами, из уравнения (9) получим ускорение а системы грузов под действием перегрузка массой m:
а модули сил натяжения нити Т1 и Т2 по обе стороны блока равны:
Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11). Равноускоренное движение системы грузов вдоль оси У описывается уравнениями движения произвольной точки системы:
где у1, v1 - начальные параметры. Исключая из этих уравнений время t при условии v1 = 0, получим
Система грузов перемещается на величину В точке с координатой у2 и скоростью v2 перегрузок подхватывается столиком и система грузов движется равномерно, перемещаясь на величину L2 за время t, измеряемое миллисекундомером экспериментальной установки. Подставляя в равенство (14) формулу
При изменении L2 меняется время t, измеряемое секундомером, но ускорение а должно оставаться неизменным. Уравнение (15) проверяется экспериментально в упражнении №1.
К основанию 1 экспериментальной установки (см.рис.3), которая стоит на регулируемых ножках 2, прикреплены миллисекундомер 3 и вертикальная стойка 4. К стойке крепятся три кронштейна, из которых два неподвижные - нижний 5 и верхний 6. А средний кронштейн 7 может перемещаться вдоль стойки. На кронштейне 7 находятся первый фотоэлектрический датчик 8 и столик 9 для снятия перегрузка. На нижнем кронштейне 5 установлен второй фотоэлектрический датчик 10 и амортизаторы 11. Все кронштейны содержат прорезь для определения положения кронштейна на вертикальной шкале 12. На верхнем конце стойки находится неподвижный блок 13. Для наблюдения ускоренного движения грузов на правый груз 15 помещают перегрузок 16 и поднимают их в такое положение, в котором нижнее основание груза совпадает с чертой на верхнем кронштейне. После начинается ускоренное движение грузов и перегрузка до того момента, когда столик 9 подхватит перегрузок. Одновременно фотоэлектрический датчик 8 включает миллисекундомер, измеряющий время равномерного движения грузов до тех пор, пока груз 15 не ударится об амортизатор II и не вызовет срабатывание датчика 10, выключающего миллисекундомер. Итак, во время равноускоренного движения грузы проходят расстояние L1 (см.рис.2) и приобретают скорость v2, с которой, двигаясь равномерно, проходят расстояние L2 за время t, измеренное миллисекундомером. Для подготовки прибора к следующему измерению нажимают кнопку "СБРОС".
Порядок выполнения работы
Теоретические основы работы
На основании закона сохранения и превращения энергии при взаимодействии тел силами упругости изменение потенциальной энергии растянутой пружины должно быть равно изменению кинетической энергии связанного с ней тела, взятому с противоположным знаком:
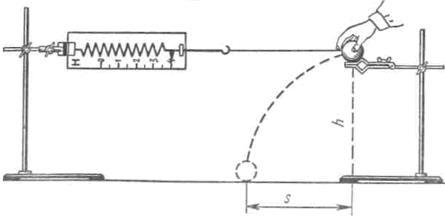
Для экспериментальной проверки этого утверждения можно воспользоваться установкой, изображенной на рисунке 1. В лапке штатива закрепляют динамометр. К его крючку привязывают шар на нити длиной 60—80 см. На другом штативе на одинаковой высоте с динамометром укрепляют в лапке желоб. Установив шар на краю желоба и удерживая его, отодвигают второй штатив от первого на длину нити. Если отодвинуть шар от края желоба на х, то в результате деформации пружина приобретет запас потенциальной энергии
где k — жесткость пружины. Затем шар отпускают. Под действием силы упругости шар приобретает скорость V. Пренебрегая потерями, вызванными действием силы трения, можно считать, что потенциальная энергия растянутой пружины полностью превратится в кинетическую энергию шара:
Скорость шара можно определить, измерив дальность его полета S при свободном падении с высоты h. Из выражений
Целью работы является проверка равенства:
С учетом равенства
Порядок выполнения работы 1.Укрепите на штативах динамометр и желоб на одинаковой Расстояние между штативами должно быть таким, чтобы шар находился на краю желоба при натянутой нити и отсутствии деформации пружины динамометра. 2. Отодвигайте шар от края желоба до тех пор, пока показания Опыт повторите не менее 10 раз. Определите среднее значение дальности полета S cp. 3. Измерьте деформацию х пружины динамометра при силе упругости Fy= 2 Н. Вычислите потенциальную энергию растянутой пружины. 4. Измерьте массу шара с помощью весов и вычислите увеличение его кинетической энергии. 5. Результаты измерений и расчетов занесите в отчетную таблицу.
Отчетная таблица
6. Оцените границы погрешностей измерения потенциальной энергии растянутой пружины Так как
Граница абсолютной погрешности равна:
7. Оцените границы погрешностей измерения кинетической энергии шара. Так как
Погрешностями εm, εg и εh, по сравнению с погрешностью ε s можно пренебречь. В этом случае Условия эксперимента по измерению дальности полета таковы, что отклонения результатов отдельных измерений от среднего значительно выше границы систематической погрешности ( Граница случайной погрешности среднего арифметического при небольшом числе измерений N находится по формуле:
где
Таким образом,
Граница абсолютной погрешности измерения кинетической энергии шара равна:
7. Сделайте вывод о выполнении закона сохранения энергии, проверив, имеют ли общие точки интервалы
Контрольные вопросы
1. Дайте определение энергии. 2. Что называется кинетической энергией? 3. Выразите кинетическую энергию через импульс тела. 4. Какие силы называются консервативными? 5. Что называется потенциальной энергией? 6. Запишите выражение для потенциальной энергии поднятого над поверхностью Земли тела и сжатой пружины. 7. Сформулируйте закон сохранения полной механической энергии. 8. При каких случаях выполняется закон сохранения механической энергии? 9. Выполняется ли закон сохранения полной механической энергии в замкнутой системе, в которой действуют только сила тяготения и силы упругости. 10. Чем можно объяснить неточное равенство изменений потенциальной энергии пружины и кинетической энергии шара?
Две пружины с коэффициентами жесткости k1 и k2 соединяют один раз последовательно, а другой раз – параллельно. Какой должна быть жесткость k пружины, которой можно было бы заменить эту систему из двух пружин? Первоначальная длина пружин одинакова.
Лабораторная работа № 4 Теоретические основы работы
Второй закон Ньютона для вращательного движения имеет вид:
где L – момент импульса тела, величина равная произведению момента инерции тела угловую скорость Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции относительно некоторой оси равен сумме произведений элементарных масс на квадрат расстояний до этой оси. Моменты инерций однородных тел простейшей формы легко выражаются через массу и геометрические характеристики.
Порядок выполнения работы
1. Надев нитяную или проволочную петлю на штифты грузов, установите их симметрично относительно оси вращения. Измерьте расстояние r1 от оси до центра масс каждого из грузов. 2. Приведите систему во вращение, удерживая петлей грузы на расстоянии r1 от оси вращения, и измерьте время t1, необходимое для совершения системой пяти оборотов. 3. Сдерните петлю и измерьте новое время t2, необходимое для совершения системой пяти оборотов. 4. Измерьте расстояние r2 от центра масс каждого груза до оси вращения. 5. Повторите опыт еще 2 раза. Результаты измерений и вычислений занесите в отчетную таблицу.
Отчетная таблица
6. Оцените границы погрешностей измерений величин Контрольные вопросы
1. Поясните принцип действия установки, использованной в работе. 2. Укажите основные причины, которые приводят к погрешностям при выполнении этой работы, а также способы уменьшения этих погрешностей. 3. Изменяется ли кинетическая энергия вращающейся системы тел при вдергивании нити?
Лабораторная работа № 5
ИЗМЕРЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ВРАЩАЮЩЕГОСЯ ДИСКА
Цель работы: Рассчитать кинетическую энергию диска, вращающегося с заданной угловой скоростью ω, и сравнить с кинетической энергией вращающегося диска, полученной в результате экспериментальных измерений. Оборудование: диск на оси; два скрепленных параллельно учебных динамометра; штатив; линейка; нить; секундомер; весы; гири.
Теоретические основы работы Кинетическая энергия вращающегося диска рассчитывается по формуле:
где I — момент инерции диска, ω — угловая скорость его вращения
Рис. 1
Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции относительно некоторой оси равен сумме произведений элементарных масс на квадрат расстояний до этой оси. Моменты инерций однородных тел простейшей формы легко выражаются через массу и геометрические характеристики.
Порядок выполнения работы 1. Измерьте массу диска и его радиус. 2. Рассчитайте кинетическую энергию диска, вращающегося с частотой υ 1=2с-1. 3. Раскрутите диск до частоты υ 1=2с-1 и натяните нить, перекинутую через шкив, отодвигая от диска планку с динамометрами (см. рис. 1). Сосчитайте, сколько оборотов п совершит диск от момента начала торможения до полной остановки. Во время торможения заметьте показания динамометров F1 и F2. Измерьте радиус r шкива диска. 4. Вычислите работу сил трения при торможении диска:
5. Повторите опыт и расчет при начальной частоте υ 1=2с-1. 6. Результаты измерений и расчетов занесите в отчетную таблицу.
Отчетная таблица
7. Сравните значения Ek и Aтp и сделайте вывод. Контрольные вопросы 1. Поясните принцип действия установки, используемой в работе. 2. Зависит ли работа, совершенная силами трения по торможению диска, от того, через верхний или нижний шкив переброшена нить? 3. Какими еще способами можно экспериментально измерить кинет
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 3151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.37.129 (0.015 с.) |


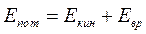
 (1)
(1)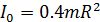 — момент инерции шара относительно оси, проходящей через центр масс (т — масса, R — радиус шара).
— момент инерции шара относительно оси, проходящей через центр масс (т — масса, R — радиус шара). ,
, , M – момент сил
, M – момент сил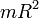



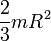


 Так как шар катится по желобу прямоугольного сечения, его угловую скорость следует вычислять по формуле
Так как шар катится по желобу прямоугольного сечения, его угловую скорость следует вычислять по формуле  (рис. 1).
(рис. 1). ,
, , т.е.
, т.е.  рис.1
рис.1



 м/с
м/с
 м/с
м/с

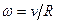 , где R — радиус шара?
, где R — радиус шара?
 Материальной точкой называется тело, размеры которого много меньше масштаба движения. Положение материальной точки в пространстве характеризует ее радиус-вектор
Материальной точкой называется тело, размеры которого много меньше масштаба движения. Положение материальной точки в пространстве характеризует ее радиус-вектор  , проведенный из начала координат к этой точке. При движении материальной точки по траектории ее радиус-вектор меняется. Мерой изменения радиуса-вектора со временем является физическая величина - скорость
, проведенный из начала координат к этой точке. При движении материальной точки по траектории ее радиус-вектор меняется. Мерой изменения радиуса-вектора со временем является физическая величина - скорость  , а мерой изменения скорости со временем - ускорение
, а мерой изменения скорости со временем - ускорение  . Мерой действия одного тела на другое является физическая величина - сила
. Мерой действия одного тела на другое является физическая величина - сила  . Основные законы динамики материальных точек - это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого имеет вид:
. Основные законы динамики материальных точек - это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого имеет вид: , (1)
, (1) , а на блок - силой
, а на блок - силой  . Тогда на каждый груз действует сила тяжести
. Тогда на каждый груз действует сила тяжести 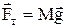 и сила натяжения нити
и сила натяжения нити  , (2)
, (2) . (3)
. (3) , (4)
, (4) - алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I - момент инерции блока; e - угловое ускорение.
- алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I - момент инерции блока; e - угловое ускорение. , (4¢)
, (4¢) , т.е.
, т.е. 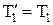 ;
;  . (5)
. (5) . (6)
. (6) или
или  . (7)
. (7) (8)
(8)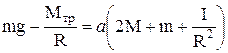 . (9)
. (9) <<
<<  . (10)
. (10) <<
<< 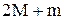 . (11)
. (11) , (12)
, (12) . (13)
. (13) ,
, ,
, . (14)
. (14) , двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).
, двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12). , получим
, получим . (15)
. (15) ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ .
.

 и
и  следует, что
следует, что  . Тогда
. Тогда

 получим:
получим:
 , то граница относительной погрешности равна:
, то граница относительной погрешности равна: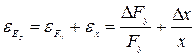

 , то граница относительной погрешности равна:
, то граница относительной погрешности равна:

 ), поэтому можно принять, что (
), поэтому можно принять, что ( ).
). ,
,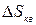 рассчитывается по формуле
рассчитывается по формуле .
.

 и
и  .
.


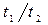
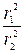 и
и  и сделайте вывод о выполнении закона сохранения момента импульса.
и сделайте вывод о выполнении закона сохранения момента импульса.