Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение закона сохранения момента импульсаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
. Цель работы: убедиться на опыте в справедливости закона сохранения момента импульса.
Оборудование: стержень на оси; два груза, скользящие по стержню; нить; секундомер; линейка; весы учебные; гири; проволока
Теоретические основы работы
Второй закон Ньютона для вращательного движения имеет вид:
где L – момент импульса тела, величина равная произведению момента инерции тела угловую скорость Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции относительно некоторой оси равен сумме произведений элементарных масс на квадрат расстояний до этой оси. Моменты инерций однородных тел простейшей формы легко выражаются через массу и геометрические характеристики.
Моменты инерции однородных тел простейшей формы относительно некоторых осей
При вращении тела вокруг оси момент импульса тела L сохраняется, если момент М внешних сил относительно этой оси равен нулю:
Для проверки этого закона применяется установка, изображенная на рисунке 1.
На легкий стержень, который с малым трением может вращаться вокруг вертикальной оси, на одинаковом расстоянии от оси вращения надеты два груза равной массы. Грузы удерживаются на заданном расстоянии нитяной или проволочной петлей. Если привести стержень с грузами во вращение с угловой скоростью ω1, то приобретенный момент импульса системы будет определяться выражением:
где
В данной установке массы стержня и грузов подобраны так, чтобы моментом инерции стержня по сравнению с моментом инерции грузов можно было пренебречь. В этом случае Угловую скорость вращения системы ω1 определим, зная время t1, необходимое для совершения грузами пяти оборотов:
При сдергивании нитяной или проволочной петли, удерживающей грузы, момент инерции системы тел увеличивается за счет того, что грузы расходятся до концов стержня. Угловая скорость системы при этом уменьшается. Момент импульса системы L2 можно определить, как и в первом случае, по формуле:
Сравнивая значения величин L1 и L2, можно экспериментально проверить закон сохранения момента импульса. Из равенства L1=L2 следует:
Так как Таким образом, для проверки закона сохранения момента импульса достаточно проверить выполнение равенства
где t1 и t2 — время, необходимое для совершения одинакового числа оборотов стержнем до и после сдергивания петли.
Порядок выполнения работы
1. Надев нитяную или проволочную петлю на штифты грузов, установите их симметрично относительно оси вращения. Измерьте расстояние r1 от оси до центра масс каждого из грузов. 2. Приведите систему во вращение, удерживая петлей грузы на расстоянии r1 от оси вращения, и измерьте время t1, необходимое для совершения системой пяти оборотов. 3. Сдерните петлю и измерьте новое время t2, необходимое для совершения системой пяти оборотов. 4. Измерьте расстояние r2 от центра масс каждого груза до оси вращения. 5. Повторите опыт еще 2 раза. Результаты измерений и вычислений занесите в отчетную таблицу.
Отчетная таблица
6. Оцените границы погрешностей измерений величин Контрольные вопросы
1. Поясните принцип действия установки, использованной в работе. 2. Укажите основные причины, которые приводят к погрешностям при выполнении этой работы, а также способы уменьшения этих погрешностей. 3. Изменяется ли кинетическая энергия вращающейся системы тел при вдергивании нити?
Лабораторная работа № 5
ИЗМЕРЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ВРАЩАЮЩЕГОСЯ ДИСКА
Цель работы: Рассчитать кинетическую энергию диска, вращающегося с заданной угловой скоростью ω, и сравнить с кинетической энергией вращающегося диска, полученной в результате экспериментальных измерений. Оборудование: диск на оси; два скрепленных параллельно учебных динамометра; штатив; линейка; нить; секундомер; весы; гири.
Теоретические основы работы Кинетическая энергия вращающегося диска рассчитывается по формуле:
где I — момент инерции диска, ω — угловая скорость его вращения
Рис. 1
Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции относительно некоторой оси равен сумме произведений элементарных масс на квадрат расстояний до этой оси. Моменты инерций однородных тел простейшей формы легко выражаются через массу и геометрические характеристики.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 752; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.146.108 (0.011 с.) |

 ,
, , M – момент сил.
, M – момент сил.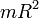



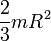


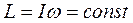 , если M= 0.
, если M= 0.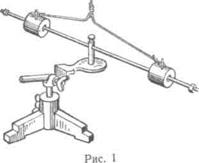
 ,
, – момент инерции груза относительно оси вращения (т — масса груза, r1 — расстояние от оси вращения до центра масс каждого из грузов),
– момент инерции груза относительно оси вращения (т — масса груза, r1 — расстояние от оси вращения до центра масс каждого из грузов),  — момент инерции стержня относительно оси, проходящей через его середину (тс — масса стержня, l — его длина).
— момент инерции стержня относительно оси, проходящей через его середину (тс — масса стержня, l — его длина). .
.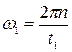 (n =5 об).
(n =5 об). .
. ,
,  .
. , то получим, что
, то получим, что  , или
, или  .
.
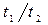
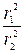 и
и  и сделайте вывод о выполнении закона сохранения момента импульса.
и сделайте вывод о выполнении закона сохранения момента импульса.