
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет и измерение скорости шара, скатывающегося по наклонному желобуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: Рассчитать конечную скорость шара, скатывающегося с наклонного желоба. Результат расчета проверить экспериментально.
Оборудование: штатив; длинный желоб с углом раствора 90°; шар радиусом R, меньшим ширины l одной стороны желоба; линейка измерительная; секундомер.
Теоретические основы работы
Для шара, скатывающегося с наклонного желоба высотой h, на основании закона сохранения энергии можно записать:
где т — масса шара, v и ω — линейная и угловая скорости шара в данный момент времени,
Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции относительно некоторой оси равен сумме произведений элементарных масс на квадрат расстояний до этой оси. Моменты инерций однородных тел простейшей формы легко выражаются через массу и геометрические характеристики. Второй закон Ньютона для вращательного движения имеет вид:
где L – момент импульса тела, величина равная произведению момента инерции тела на угловую скорость
Моменты инерции однородных тел простейшей формы относительно некоторых осей
Из рисунка видно, что при
Следовательно, первое равенство можно записать в виде:
Откуда
Поскольку скорость шара в любой момент времени пропорциональна корню квадратному из высоты h, движение шара — равноускоренное.
Порядок выполнения работы
1. С помощью уровня или шара установите горизонтальность поверхности стола. 2. С помощью штатива установите желоб в наклонном положении (рис. 2). Измерьте высоту h наклонного желоба. 3. Рассчитайте теоретическую скорость скатывания шара с желоба по формуле:
4. Измерьте длину l желоба и время t скатывания с него шара. 5. Рассчитайте скорость шара в конце желоба по формуле:
6. Повторите опыт при разных значениях высоты h наклонного желоба и сделайте вывод об оптимальных условиях выполнения работы. 7. Результаты измерений и расчетов занесите в отчетную таблицу.
Отчетная таблица
8. Рассчитайте погрешности измерений vT и vэ иубедитесь в достоверности измерений.
Рис. 2
Контрольные вопросы
1. Сформулируйте закон сохранения полной механической энергии. 2. Назовите условия при которых выполняется закон сохранения полной механической энергии. 3. Дайте определение момента инерции. 4. Почему при скатывании шара по желобу нельзя использовать формулу 5. Как доказать, что движение шара по желобу равноускоренное? 6. Чем объясняются различия в значениях v т и vэ, полученных в данной работе? 7. При каких углах наклона желоба погрешности измерений минимальны? 8. Какую роль играет трение в данном опыте? 9. Колесо катилось по столу со скоростью 0,6 м/с. Достигнув края стола стало падать. Определить скорость краевой точки через 0,02 с от начала падения (в этот момент её линейная скорость вращения направлена вертикально вниз). 10.Автомобиль движется со скоростью 10 м/с. Определить скорость относительно Земли точек A, B, C, лежащих на его ободе. 11.Два тела одновременно начинают движение по окружности из одной точки в одном направлении. Период обращения первого тела равен 3 с, второго 4 с. Через какой промежуток времени первое тело догонит второе? 12.Секундная стрелка в 2 раза короче минутной. Во сколько раз линейная скорость конца секундной стрелки больше линейной скорости минутной стрелки?
Творческий практикум Для точек земной поверхности на широте Санкт-Петербурга (60°) определите линейную скорость и ускорение, испытываемое ими вследствие суточного вращения Земли (рис. 33). Радиус Земли считайте равным 6370 км.
Лабораторная работа № 2
ИССЛЕДОВАНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ
Цель работы: Изучить равнопеременное и равномерное прямолинейные движения в поле земного тяготения. Определить ускорение свободного падения.
Оборудование: машина Атвуда.
Теоретические основы работы Механическим движением называется происходящее со временем перемещение тел или их частей относительно других тел (тел отсчета). Любое механическое движение рассматривается в определенной системе отсчета, состоящей из тела отсчета, связанной с ним системы пространственных координат и часов.
называют основным уравнением динамики. Эскиз машины Атвуда показан на рис.2. Два груза массами М соединены нитью, перекинутой через неподвижный блок. Если на один из грузов положить перегрузок массой m, то система приходит в ускоренное движение. Каждый из грузов натягивает участок нити, который, стараясь сократиться, действует на груз силой натяжения
а для другого груза:
Основное уравнение динамики вращательного движения неподвижного блока имеет вид:
где Если вращение по часовой стрелке считать положительным, то, согласно рис.2, получим
где R - радиус блока; Мтр - момент силы трения. Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:
Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:
Наконец, в отсутствие скольжения нити по блоку ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:
Проецируя уравнения (2) и (3) на ось У, направленную вертикально вверх, получим с учетом формул (5), (6) и (7) систему уравнений, к которой присоединим уравнение (4¢):
Умножая первое из уравнений (8) на -1 и складывая все уравнения (8), получим
В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство
Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:
Пренебрегая малыми величинами, из уравнения (9) получим ускорение а системы грузов под действием перегрузка массой m:
а модули сил натяжения нити Т1 и Т2 по обе стороны блока равны:
Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11). Равноускоренное движение системы грузов вдоль оси У описывается уравнениями движения произвольной точки системы:
где у1, v1 - начальные параметры. Исключая из этих уравнений время t при условии v1 = 0, получим
Система грузов перемещается на величину В точке с координатой у2 и скоростью v2 перегрузок подхватывается столиком и система грузов движется равномерно, перемещаясь на величину L2 за время t, измеряемое миллисекундомером экспериментальной установки. Подставляя в равенство (14) формулу
При изменении L2 меняется время t, измеряемое секундомером, но ускорение а должно оставаться неизменным. Уравнение (15) проверяется экспериментально в упражнении №1.
К основанию 1 экспериментальной установки (см.рис.3), которая стоит на регулируемых ножках 2, прикреплены миллисекундомер 3 и вертикальная стойка 4. К стойке крепятся три кронштейна, из которых два неподвижные - нижний 5 и верхний 6. А средний кронштейн 7 может перемещаться вдоль стойки. На кронштейне 7 находятся первый фотоэлектрический датчик 8 и столик 9 для снятия перегрузка. На нижнем кронштейне 5 установлен второй фотоэлектрический датчик 10 и амортизаторы 11. Все кронштейны содержат прорезь для определения положения кронштейна на вертикальной шкале 12. На верхнем конце стойки находится неподвижный блок 13. Для наблюдения ускоренного движения грузов на правый груз 15 помещают перегрузок 16 и поднимают их в такое положение, в котором нижнее основание груза совпадает с чертой на верхнем кронштейне. После начинается ускоренное движение грузов и перегрузка до того момента, когда столик 9 подхватит перегрузок. Одновременно фотоэлектрический датчик 8 включает миллисекундомер, измеряющий время равномерного движения грузов до тех пор, пока груз 15 не ударится об амортизатор II и не вызовет срабатывание датчика 10, выключающего миллисекундомер. Итак, во время равноускоренного движения грузы проходят расстояние L1 (см.рис.2) и приобретают скорость v2, с которой, двигаясь равномерно, проходят расстояние L2 за время t, измеренное миллисекундомером. Для подготовки прибора к следующему измерению нажимают кнопку "СБРОС".
Порядок выполнения работы
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1038; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.251.204 (0.009 с.) |

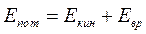
 (1)
(1)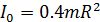 — момент инерции шара относительно оси, проходящей через центр масс (т — масса, R — радиус шара).
— момент инерции шара относительно оси, проходящей через центр масс (т — масса, R — радиус шара). ,
, , M – момент сил
, M – момент сил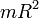



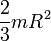


 Так как шар катится по желобу прямоугольного сечения, его угловую скорость следует вычислять по формуле
Так как шар катится по желобу прямоугольного сечения, его угловую скорость следует вычислять по формуле  (рис. 1).
(рис. 1). ,
, , т.е.
, т.е.  рис.1
рис.1



 м/с
м/с
 м/с
м/с

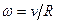 , где R — радиус шара?
, где R — радиус шара?
 Материальной точкой называется тело, размеры которого много меньше масштаба движения. Положение материальной точки в пространстве характеризует ее радиус-вектор
Материальной точкой называется тело, размеры которого много меньше масштаба движения. Положение материальной точки в пространстве характеризует ее радиус-вектор  , проведенный из начала координат к этой точке. При движении материальной точки по траектории ее радиус-вектор меняется. Мерой изменения радиуса-вектора со временем является физическая величина - скорость
, проведенный из начала координат к этой точке. При движении материальной точки по траектории ее радиус-вектор меняется. Мерой изменения радиуса-вектора со временем является физическая величина - скорость  , а мерой изменения скорости со временем - ускорение
, а мерой изменения скорости со временем - ускорение  . Мерой действия одного тела на другое является физическая величина - сила
. Мерой действия одного тела на другое является физическая величина - сила  . Основные законы динамики материальных точек - это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого имеет вид:
. Основные законы динамики материальных точек - это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого имеет вид: , (1)
, (1) , а на блок - силой
, а на блок - силой  . Тогда на каждый груз действует сила тяжести
. Тогда на каждый груз действует сила тяжести 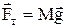 и сила натяжения нити
и сила натяжения нити  , (2)
, (2) . (3)
. (3) , (4)
, (4) - алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I - момент инерции блока; e - угловое ускорение.
- алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I - момент инерции блока; e - угловое ускорение. , (4¢)
, (4¢) , т.е.
, т.е. 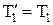 ;
;  . (5)
. (5) . (6)
. (6) или
или  . (7)
. (7) (8)
(8)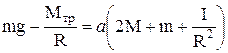 . (9)
. (9) <<
<<  . (10)
. (10) <<
<< 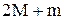 . (11)
. (11) , (12)
, (12) . (13)
. (13) ,
, ,
, . (14)
. (14) , двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).
, двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12). , получим
, получим . (15)
. (15) ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ


