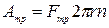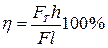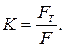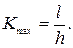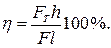Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моменты инерции однородных тел простейшей формы относительно некоторых осейСодержание книги
Поиск на нашем сайте
Момент инерции диска равен:
Кинетическую энергию вращающегося диска можно определить экспериментально. Для этого надо измерить работу, которая совершается при торможении диска до полной остановки:
где Fтp — сила трения, под действием которой останавливается диск, l – путь, на котором действует сила трения. В данной работе торможение диска осуществляется с помощью нити, перекинутой через шкив диска. Концы нити прикреплены к двум динамометрам, расположенным горизонтально (рис. 1). Вследствие трения нити о шкив диска динамометры дают разные показания F1 и F2. Разность этих показаний равна силе трения:
Сила трения действует на пути l, равном произведению длины окружности шкива на число оборотов п, совершаемых диском при торможении до полной остановки. Тогда
Порядок выполнения работы 1. Измерьте массу диска и его радиус. 2. Рассчитайте кинетическую энергию диска, вращающегося с частотой υ 1=2с-1. 3. Раскрутите диск до частоты υ 1=2с-1 и натяните нить, перекинутую через шкив, отодвигая от диска планку с динамометрами (см. рис. 1). Сосчитайте, сколько оборотов п совершит диск от момента начала торможения до полной остановки. Во время торможения заметьте показания динамометров F1 и F2. Измерьте радиус r шкива диска. 4. Вычислите работу сил трения при торможении диска:
5. Повторите опыт и расчет при начальной частоте υ 1=2с-1. 6. Результаты измерений и расчетов занесите в отчетную таблицу.
Отчетная таблица
7. Сравните значения Ek и Aтp и сделайте вывод. Контрольные вопросы 1. Поясните принцип действия установки, используемой в работе. 2. Зависит ли работа, совершенная силами трения по торможению диска, от того, через верхний или нижний шкив переброшена нить? 3. Какими еще способами можно экспериментально измерить кинетическую энергию вращающегося диска? 4. Укажите основные причины, которые приводят к погрешностям при выполнении работы, а также способы уменьшения этих погрешностей. 5. Запишите второй закон Ньютона для вращательного движения. 6. Какие силы называются внутренними силами системы? 7. Какие силы называются внешними силами системы? 8. Какая система называется замкнутой? 9. Сформулируйте закон созранения энергии для замкнутой системы. 10.Какие силы называются консервативными? 11.Чему равна работа консервативных сил? Творческий практикум Предложите способ внесения поправки при измерении кинетической энергии предложенным способом, с помощью которого учитывалась бы работа сил трения в оси диска. Проверьте свой способ на опыте. Лабораторная работа № 6
ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ. ИЗМЕРЕНИЕ КПД НАКЛОННОЙ ПЛОСКОСТИ
Цель работы: исследовать зависимость КПД наклонной плоскости и выигрыша в силе, получаемого с ее помощью, от угла наклона плоскости к горизонту.
Оборудование: деревянная доска; деревянный брусок; штатив; динамометр; линейка измерительная.
Теоретические основы работы
КПД любого простого механизма равен отношению полезной работы Aпол к совершенной работе Асов. КПД обычно выражается в процентах:
При отсутствии трения КПД простого механизма, втом числе и наклонной плоскости, равен единице. В этом случае работа, совершенная силой F, приложенной к телу и направленной вдоль наклонной плоскости вверх, равна полезной работе:
Обозначив путь, пройденный телом вдоль наклонной плоскости, через l, высоту подъема – h, получим: Fl = Fτh. При этом выигрыш в силе равен
В реальных условиях действие силы трения снижает КПД наклонной плоскости и уменьшает выигрыш в силе. Для определения КПД наклонной плоскости и выигрыша всиле, полученного с ее помощью, следует использовать выражения:
Целью работы является измерение КПД наклонной плоскости и выигрыша в силе при разных углах α ее наклона к горизонту.
Порядок выполнения работы
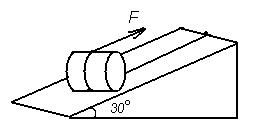
1. Соберите установку по рисунку 1. Измерьте высоту h (α1 = 30°) и длину l наклонной плоскости (рис. 2). 2. Вычислите максимально возможное значение выигрыша всиле, получаемого при заданном наклоне плоскости:
3. Положите брусок на наклонную плоскость. Прикрепив к нему динамометр, равномерно тяните его вверх вдоль наклонной плоскости. Измерьте силу F. 4. Измерьте с помощью динамометра силу тяжести FT, действующую на брусок, и найдите экспериментальное значение выигрыша в силе, полученного с помощью наклонной плоскости:
5. Вычислите КПД наклонной плоскости при заданном угле
6. Повторите измерения при углах наклона плоскости, рав 7. Результаты измерений и расчетов занесите в отчетную Отчетная таблица
Дополнительное задание
Получите теоретическую зависимость η(α) и K(α) и сравните ее с результатами эксперимента.
Контрольные вопросы
1. С какой целью применяют наклонную плоскость? 2. Каким образом можно увеличить КПД наклонной плоскости? 3. Каким образом можно увеличить выигрыш в силе, получаемый с помощью наклонной плоскости? 4. Зависит ли КПД наклонной плоскости от массы груза? 5. Объясните зависимость КПД наклонной плоскости и выигрыша в силе, получаемого с ее помощью, от угла наклона плоскости. 6. Дать определение понятия «простой механизм». 7. Дать определение понятия «выигрыш в силе». 8. Сформулировать золотое правило механики. 9. Лебедка равномерно поднимает груз массой 200 кг. На высоту 3 м. за 5 сек. Найдите работу силы тяжести. 10. Лебедка равномерно поднимает груз массой 200 кг. На высоту 3 м. за 5 сек. Найдите работу силы тяги. 11. Лебедка равномерно поднимает груз массой 200 кг. На высоту 3 м. за 5 сек. Вычислите кинетическую энергию. 12. Лебедка равномерно поднимает груз массой 200 кг. На высоту 3 м. за 5 сек. Вычислите потенциальную энергию. 13. Груз массой 40 кг. поднимают с помощью подвижного блока. На какую длину надо вытянуть свободный конец веревки, чтобы поднять груз на высоту 120 см. 14. Груз массой 40 кг. поднимают с помощью подвижного блока. Найдите работу, производимую рабочим при подъеме груза на 120 см., если сила, приложенная к веревке 250 Н. Каков КПД блока.
Творческий практикум 1. Определить КПД различных механизмов и простых машин
2. По наклонной плоскости при помощи веревки поднимают бочку. Какой выигрыш в силе получают при таком подъеме?
3. Используя стальной лом в качестве рычага, на одну и ту же высоту поднимают груз Р двумя способами (рис. а и б). Плечи, на которые действует груз, и трение в точках опоры О одинаковы. Одинаковым ли будет КПД рычагов? Ответ объясните.
Лабораторная работа № 7
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 790; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.168.219 (0.009 с.) |

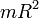



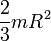


 , где т – масса диска, R – его радиус.
, где т – масса диска, R – его радиус.

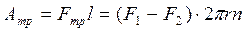 (r — радиус шкива).
(r — радиус шкива).